Содержание
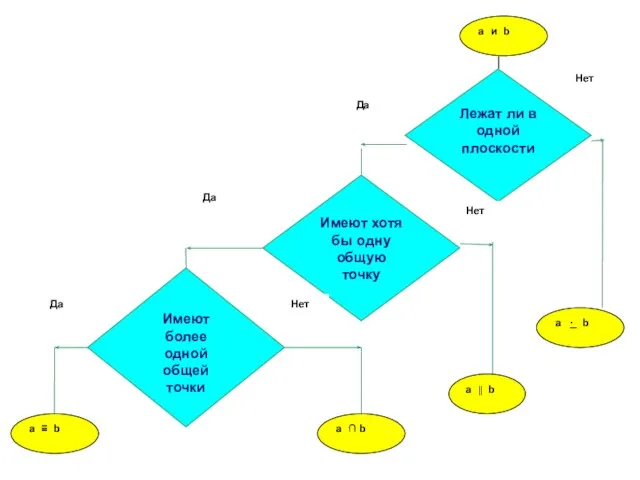
- 2. Определение Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
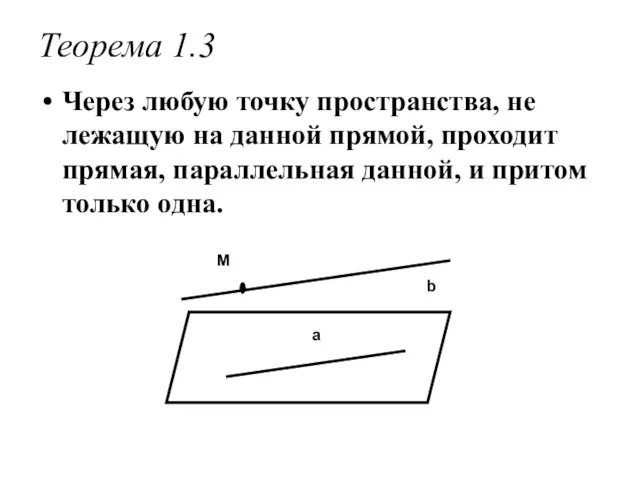
- 3. Теорема 1.3 Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и
- 4. Определение Две прямые называются скрещивающимися, если они не лежат в одной плоскости.
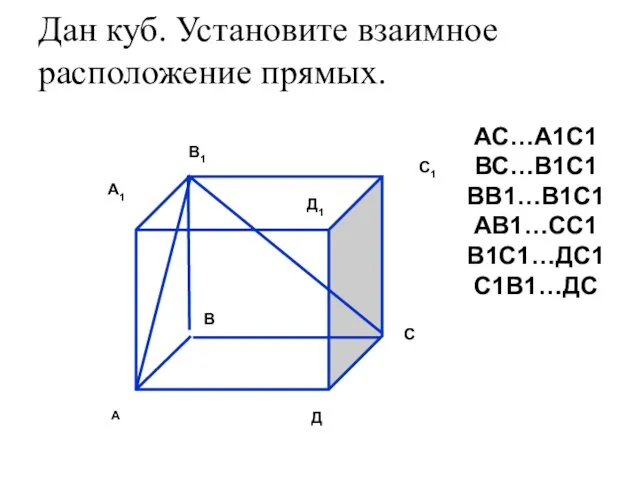
- 6. Дан куб. Установите взаимное расположение прямых. АС…А1С1 ВС…В1С1 ВВ1…В1С1 АВ1…СС1 В1С1…ДС1 С1В1…ДС
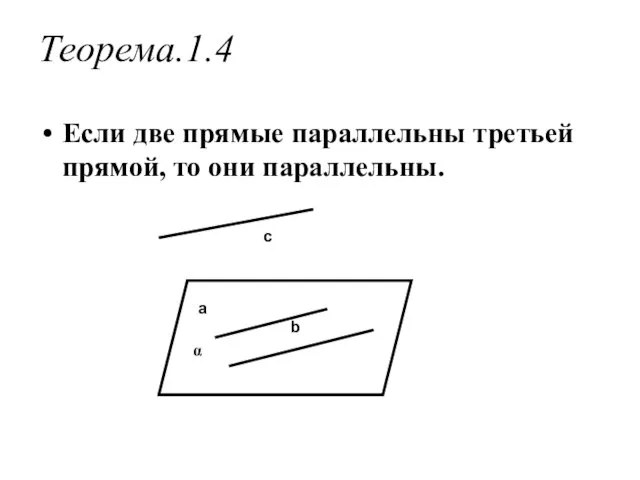
- 7. Теорема.1.4 Если две прямые параллельны третьей прямой, то они параллельны.
- 8. Теорема1.5 Если прямая, не лежащая в данной плоскости параллельна какой-нибудь прямой, лежащей в этой плоскости, то
- 9. Утверждение 1. Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то
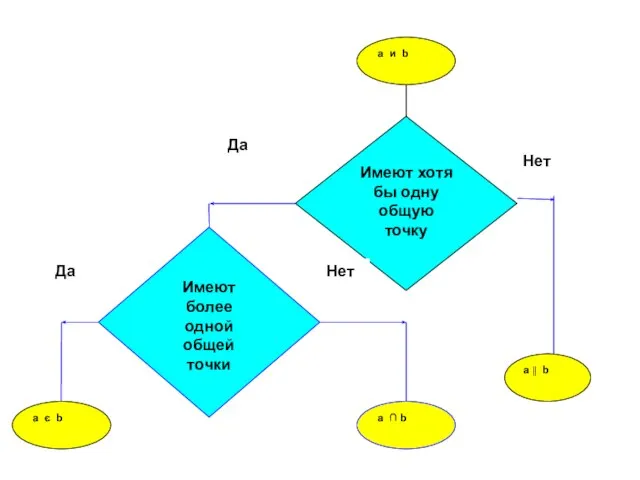
- 10. Взаимное расположение прямой и плоскости
- 12. Определение Прямая и плоскость называются параллельными, если они не имеют общих точек.
- 13. Тема урока Скрещивающиеся прямые. Угол с сонаправленными сторонами. Угол между прямыми
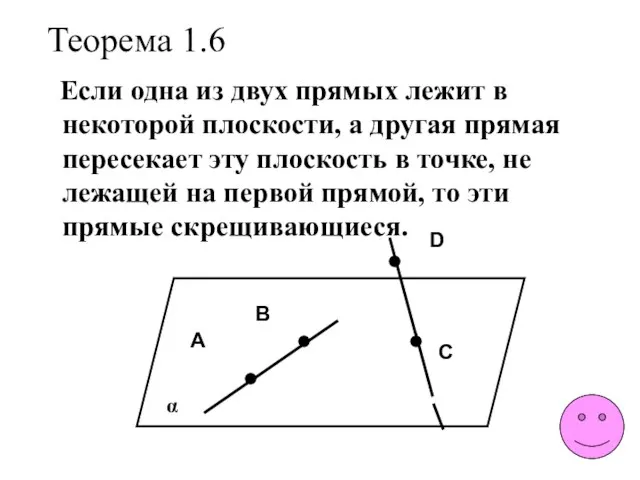
- 14. Теорема 1.6 Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту
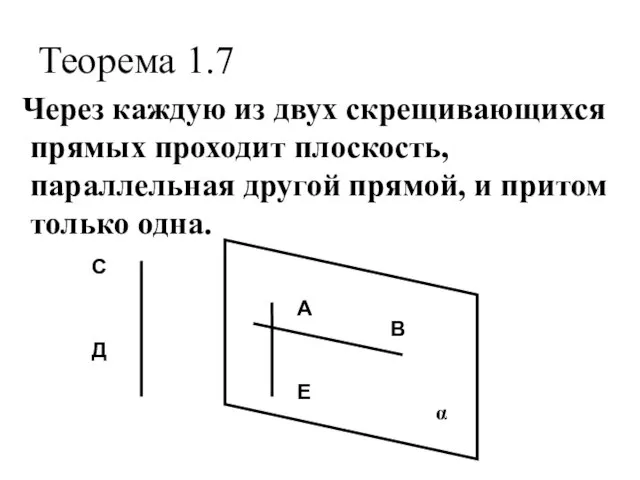
- 15. Теорема 1.7 Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только
- 16. Определение Два луча ОА и О1А1, не лежащие на одной прямой, называются сонаправленными, если они параллельны
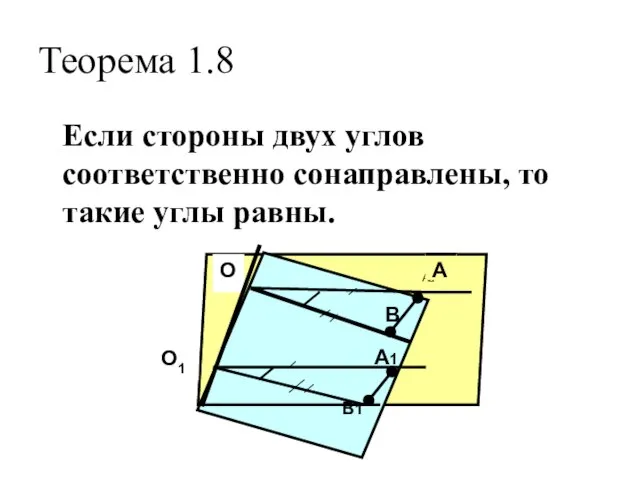
- 17. Теорема 1.8 Если стороны двух углов соответственно сонаправлены, то такие углы равны. В А1 В1
- 19. Скачать презентацию








 Дискретные случайные величины
Дискретные случайные величины Решение тригонометрического уравнения
Решение тригонометрического уравнения Внеклассное мероприятие. Путешествие в мир многогранников
Внеклассное мероприятие. Путешествие в мир многогранников Задачи на расстояние
Задачи на расстояние Параллельность_прямых_в_пространстве_2019
Параллельность_прямых_в_пространстве_2019 Дроби. 5 класс
Дроби. 5 класс Производная частного двух функций
Производная частного двух функций Арифметическая прогрессия. 9 класс
Арифметическая прогрессия. 9 класс Измерение параллеппипеда
Измерение параллеппипеда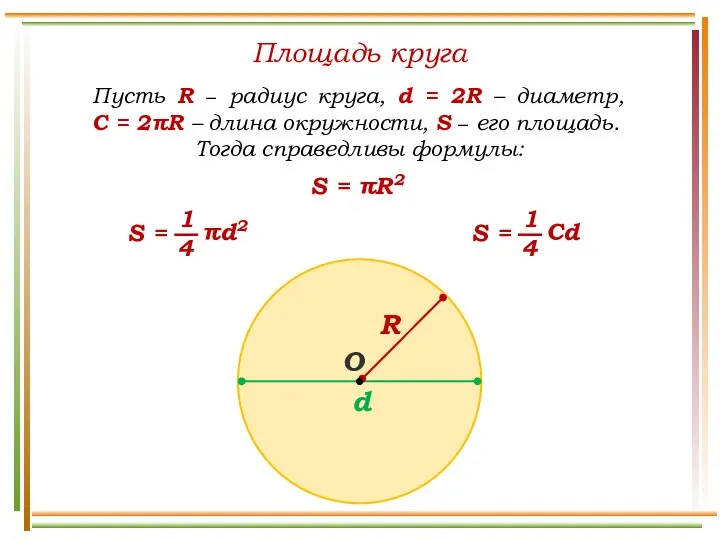 Площадь круга
Площадь круга Презентация на тему Повторение математики 5 класс
Презентация на тему Повторение математики 5 класс  Презентация на тему Решение уравнений, содержащих несколько знаков модуля
Презентация на тему Решение уравнений, содержащих несколько знаков модуля  Квадратные неравенства
Квадратные неравенства Решение интеграла
Решение интеграла Предел функции в точке
Предел функции в точке Построение треугольника
Построение треугольника Распределенные системы. Математическое представление распределенной системы
Распределенные системы. Математическое представление распределенной системы Логарифмы вокруг нас
Логарифмы вокруг нас Тригонометрия. Контрольная работа
Тригонометрия. Контрольная работа Правильные многоугольники в природе. Геометрия пчелиных сот
Правильные многоугольники в природе. Геометрия пчелиных сот Повторение 1 класс
Повторение 1 класс Задачи математической статистики
Задачи математической статистики Это страшное слово: Параметр
Это страшное слово: Параметр Линии второго порядка
Линии второго порядка Methodical Problems of Comparative Studies
Methodical Problems of Comparative Studies Финансовая грамотность
Финансовая грамотность Решение задач с помощью составления систем уравнений. 9 класс
Решение задач с помощью составления систем уравнений. 9 класс Правильные многоугольники
Правильные многоугольники