Содержание
- 2. «Математика – наука о порядке» А. Уайтхед. Обучение математике через задачи – идея далеко не новая.
- 3. Алгоритм решения систем неравенств Чтобы решить систему неравенств, надо: 1) решить каждое неравенство системы; 2) изобразить
- 4. Найти все решения системы неравенств и записать ответ с помощью числового промежутка: Блиц - опрос Ответ:
- 5. Решить систему неравенств: Решение. 1) решим каждое неравенство исходной системы, получим: : (−2), : 4; изобразим
- 6. \\\\\\\\\\\\\\\\\\ \\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ 1,5 -2 Ответ: (-2;1,5]. ,то есть
- 7. Решить систему неравенств: Решение. 1) Решим каждое из неравенств данной системы одновременно, получим: : 2, :
- 8. −3 −2 3 ○ ○ \\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ //////////////////////////////// ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| 3) Получили решение исходной системы: полуинтервал ( −2;
- 9. Решить систему неравенств: Решение. 1) Решим каждое неравенство данной системы: : 2, : (−3);
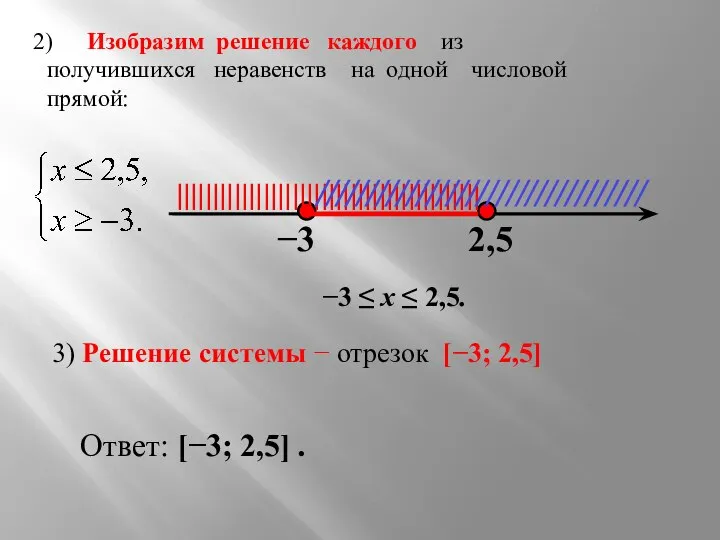
- 10. Изобразим решение каждого из получившихся неравенств на одной числовой прямой: −3 2,5 |||||||||||||||||||||||||||||||||||||||||| ///////////////////////////////// 3) Решение
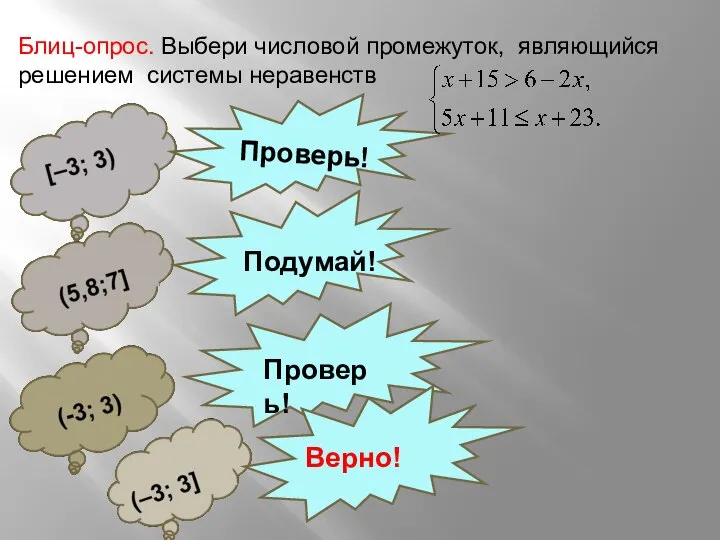
- 11. Блиц-опрос. Выбери числовой промежуток, являющийся решением системы неравенств
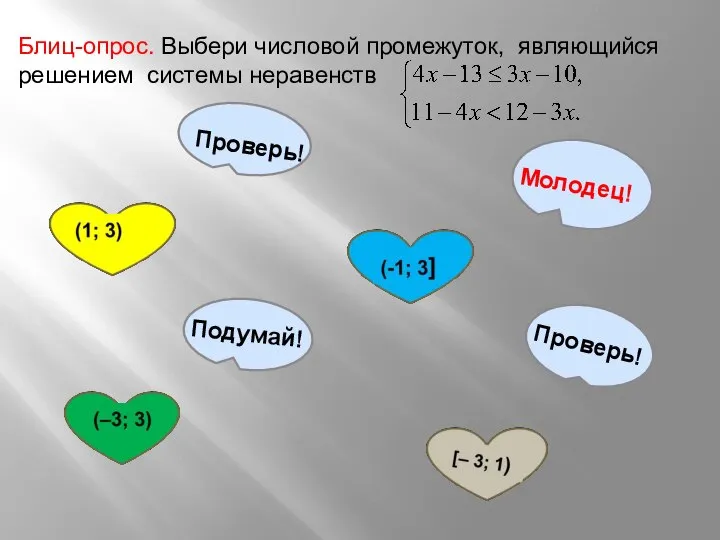
- 12. Блиц-опрос. Выбери числовой промежуток, являющийся решением системы неравенств
- 13. Блиц-опрос. Выбери наибольшее целое решение системы
- 14. Блиц-опрос. Выбери наименьшее целое решение системы
- 16. Скачать презентацию




![\\\\\\\\\\\\\\\\\\ \\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ 1,5 -2 Ответ: (-2;1,5]. ,то есть](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1082022/slide-5.jpg)





 27.09 Графики функций
27.09 Графики функций Исаак Ньютон
Исаак Ньютон Задачи на проценты
Задачи на проценты Решение уравнений и неравенств заданий С3
Решение уравнений и неравенств заданий С3 Фрактальное изображение
Фрактальное изображение Возведение в степень произведения. 7 класс
Возведение в степень произведения. 7 класс Презентация на тему Задачи на увеличение и уменьшение числа (1 класс)
Презентация на тему Задачи на увеличение и уменьшение числа (1 класс)  Сравнение обыкновенной дроби и десятичной
Сравнение обыкновенной дроби и десятичной Счёт до 9. Состав числа 9
Счёт до 9. Состав числа 9 Приёмы устных вычислений вида: 470 + 80, 560 - 90
Приёмы устных вычислений вида: 470 + 80, 560 - 90 Булевы выражения. Глава 2
Булевы выражения. Глава 2 Старинные русские меры длины в современной жизни человека
Старинные русские меры длины в современной жизни человека Презентация на тему Понятие одночлена стандартный вид одночлена (7 класс)
Презентация на тему Понятие одночлена стандартный вид одночлена (7 класс)  Задания подготовительного этапа по программе Рудницкой В.Н Начальная школа XXI века
Задания подготовительного этапа по программе Рудницкой В.Н Начальная школа XXI века Средняя квадратическая величина
Средняя квадратическая величина Деление натуральных чисел
Деление натуральных чисел Параллельность плоскостей
Параллельность плоскостей Двугранный угол. Перпендикулярность плоскостей
Двугранный угол. Перпендикулярность плоскостей Решение Уравнений, содержащих модуль
Решение Уравнений, содержащих модуль Выражение (для печатной и электронной формы учебника)
Выражение (для печатной и электронной формы учебника) Презентация по математике "Что такое понятие" -
Презентация по математике "Что такое понятие" -  По следам телепередач. Поле чудес
По следам телепередач. Поле чудес Занимательная математика
Занимательная математика Формулы сокращенного умножения. Интерактивный плакат
Формулы сокращенного умножения. Интерактивный плакат Найти точки экстремума функции
Найти точки экстремума функции Экстремум функции нескольких переменных. Наибольшее и наименьшее значение функции в замкнутой ограниченной области (тема 1.4)
Экстремум функции нескольких переменных. Наибольшее и наименьшее значение функции в замкнутой ограниченной области (тема 1.4) Площади фигур
Площади фигур Задачи. Часть 2
Задачи. Часть 2