Решение систем неравенств (8 класс)

«Математика – наука о порядке»
А. Уайтхед.
Обучение математике через задачи – идея далеко не новая. Еще Ньютон сказал: «Примеры поучают больше, чем теория».
Нужно разумно чередовать задачи, осуществляющие различную степень познавательной самостоятельности.
Работа учителя всегда была и остается творческой.

«Три пути ведут к знаниям:
путь размышления- это путь
самый благородный, путь подражания – это путь самый
легкий и путь опыта- это
путь самый горький».
Конфуций.
УМК к учебнику Ш. А. Алимова, Ю. М. Колягина и др.
Тип урока: учебный практикум.
Оборудование: магнитная доска, раздаточные таблицы, раздаточный дифференцированный
материал для обучения и развития учащихся.
Цели урока: 1. Систематизировать, расширить и углубить знания, умения учащихся применять
различные способы решения систем неравенств и их комбинаций.
2. Уметь решать системы линейных неравенств и неравенств, сводящихся к
линейным, извлекать необходимую информацию из учебно – научных текстов.
3. Знать о способах решения систем неравенств.
4. Способствовать развитию наблюдательности, умения анализировать,
сравнивать, делать выводы.
5. Владеть навыками самоанализа, самоконтроля, побуждать учащихся к
взаимоконтролю, вызывать у них потребность в обосновании своих
высказываний.

Найти все решения системы неравенств и записать ответ с помощью числового промежутка:
Ответ:
Ответ:
Ответ:
Ответ:
полуинтервал [- 3,7; 5,1)
полуинтервал (3; 7,9]
отрезок [-3,5; 2,7]
луч (3; + ∞)
Ответ: луч (- ∞;- 3,1]
Ход урока:
Организационный момент .
Проверка домашнего задания ( фронтально). Дать ответы по домашнему заданию на вопросы учащихся.
Блиц – опрос.

Алгоритм решения систем неравенств
Чтобы решить систему неравенств, надо:
1) решить каждое неравенство системы;
2) изобразить решение каждого неравенства данной системы
на одной числовой прямой.
3) записать решение системы, используя скобки, в случаях,
когда решением является отрезок, луч, интервал или
полуинтервал (решение может быть записано с помощью
простейшего неравенства)
4) записать ответ
IV. Напомним решение систем неравенств , для этого еще раз повторим алгоритм решения
систем неравенств.

1) Решить систему неравенств:
Решение. 1) решим каждое неравенство исходной системы, получим:
: (−2)
: 4
изобразим решение каждого из
получившихся неравенств на ____________
числовой прямой:
V. Выполнение упражнений.

\\\\\\\\\\\\\\\\\\
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
1,5
-2
Ответ: (-2;1,5].
,то есть

2) Решить систему неравенств:
Решение. 1) Решим каждое из неравенств данной системы одновременно, получим:
: 2,
: 3,
: 4;
Изобразим решение каждого из
получившихся неравенств на одной числовой
прямой:

−3
−2
3
○
○
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
////////////////////////////////
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3) Получили решение исходной системы: полуинтервал ( −2; 3]
Ответ: (-2;3].
−2< х ≤ 3.

3) Решить систему неравенств:
Решение. 1) Решим каждое неравенство данной системы:
: 2, : (−3);

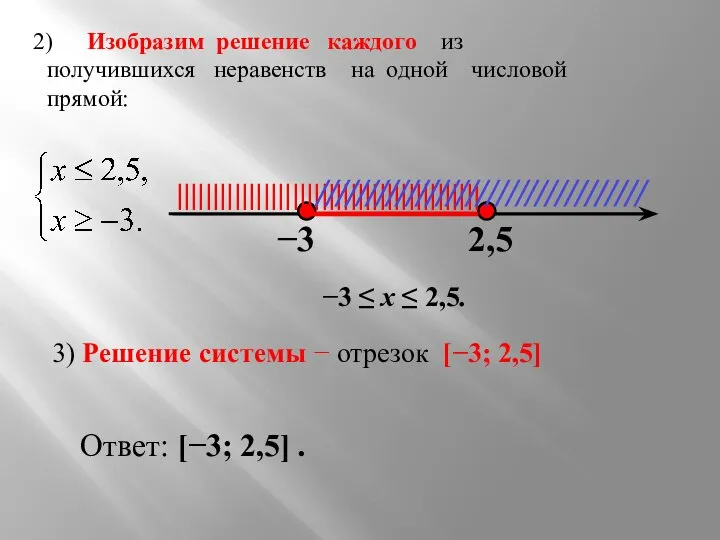
Изобразим решение каждого из
получившихся неравенств на одной числовой
прямой:
−3
2,5
||||||||||||||||||||||||||||||||||||||||||
/////////////////////////////////
3) Решение системы − отрезок [−3; 2,5]
Ответ: [−3; 2,5] .
−3 ≤ х ≤ 2,5.

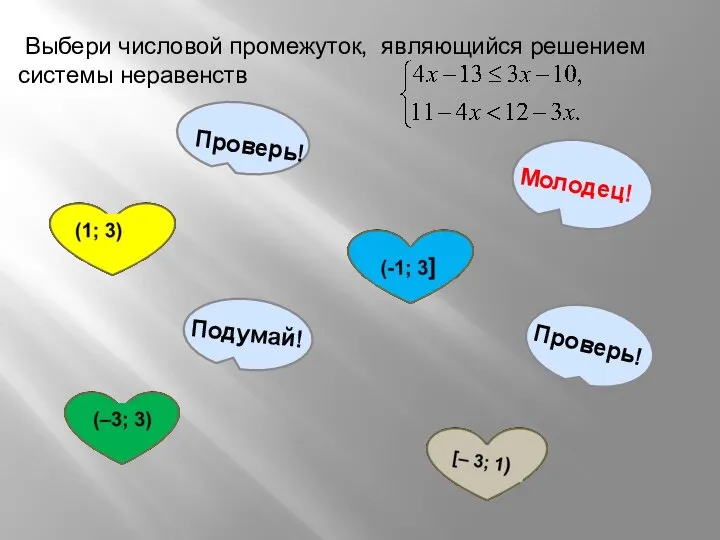
4) Подумай и реши. Выбери числовой промежуток, являющийся решением системы неравенств:

Выбери числовой промежуток, являющийся решением системы неравенств

Выбери наибольшее целое решение системы неравенств

Выбери наименьшее целое решение системы

5) Задача. Одна сторона треугольника равна 5 метрам, а другая- 8 метрам. Какой может быть третья сторона, если периметр треугольника больше 17 метров ?
Решение. Пусть x метров (x>0) — длина третьей стороны треугольника, тогда, согласно условию задачи и учитывая неравенство треугольника, составим и решим систему неравенств:
Ответ: длина третьей стороны больше 4 метров, но меньше 13 метров.
4
13
////////////////////////////////////////////////
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
4< х < 13, значит, длина третьей стороны есть любое число из интервала 4< х < 13.