Слайд 22
Литература:
Линейная алгебра
Хамидуллин Р.Я. Гулиян Б.Ш.
Занятие 3
ОБРАТНАЯ МАТРИЦА

Слайд 31.3. ОБРАТНАЯ МАТРИЦА
Матрица A-1 называется обратной к
матрице А, если
АA-1=A-1А=Е
где

Е – единичная матрица
Слайд 4Алгоритм нахождения обратной матрицы
1
Определяем, квадратная ли
матрица. Если нет, то
обратной матрицы для
нее

не существует.
ОБРАТНАЯ МАТРИЦА
Слайд 52
Находим определитель матрицы.
Если он равен нулю, то обратной
матрицы не существует.

ОБРАТНАЯ МАТРИЦА
Слайд 63
Заменяем каждый элемент
матрицы
его алгебраическим дополнением.
ОБРАТНАЯ МАТРИЦА

Слайд 74
Полученную матрицу
транспонируем.
ОБРАТНАЯ МАТРИЦА

Слайд 85
Каждый элемент
полученной матрицы делим
на определитель исходной
матрицы. Получаем
матрицу, обратную

к данной.
ОБРАТНАЯ МАТРИЦА
Слайд 96
Делаем проверку.
Для этого перемножаем
полученную и исходную матрицы.
Должна получиться

единичная матрица.
ОБРАТНАЯ МАТРИЦА
Слайд 10Пример.
Найти матрицу,
обратную к матрице А
ОБРАТНАЯ МАТРИЦА

Слайд 11Применяем алгоритм нахождения обратной матрицы.
Решение:
Находим определитель:
Матрица квадратная, следовательно обратная матрица для

нее существует.
1
2
ОБРАТНАЯ МАТРИЦА
Слайд 12Находим алгебраические дополнения каждого элемента матрицы:
3
Составляем из полученных значений матрицу:
ОБРАТНАЯ МАТРИЦА

Слайд 13Транспонируем ее:
Каждый элемент матрицы делим на определитель Δ=1 и получаем обратную матрицу:
4
5

ОБРАТНАЯ МАТРИЦА
Слайд 14Проверяем:
6
1.3. ОБРАТНАЯ МАТРИЦА














 Пропорция
Пропорция Измерение площадей. Площадь прямоугольника
Измерение площадей. Площадь прямоугольника Графики линейных функций
Графики линейных функций Центральные и вписанные углы
Центральные и вписанные углы English System of Measures
English System of Measures Функции многих переменных. Лекция 16
Функции многих переменных. Лекция 16 Геометрические преобразования в пространстве
Геометрические преобразования в пространстве История происхождения математических знаков
История происхождения математических знаков Решение тригонометрических уравнений
Решение тригонометрических уравнений بخش دوم :حل معادله درجه 2و کاربرد آن ریاضی دهم آنسانی
بخش دوم :حل معادله درجه 2و کاربرد آن ریاضی دهم آنسانی Статистика
Статистика Начерти два отрезка
Начерти два отрезка Теория вероятностей
Теория вероятностей Единица времени - секунда
Единица времени - секунда Измерение углов, расстояний. Теодолит, устройство, поверки (лекция 5)
Измерение углов, расстояний. Теодолит, устройство, поверки (лекция 5) Решение задач на временные отношения (подготовка к олимпиаде по математике обучающихся 4 класса)
Решение задач на временные отношения (подготовка к олимпиаде по математике обучающихся 4 класса) ПГНИУ-20.09.22 МЛ Л 4
ПГНИУ-20.09.22 МЛ Л 4 Геометрические фигуры (открытый урок - игра Поле чудес)
Геометрические фигуры (открытый урок - игра Поле чудес) Интегральное исчисление
Интегральное исчисление Великие математики
Великие математики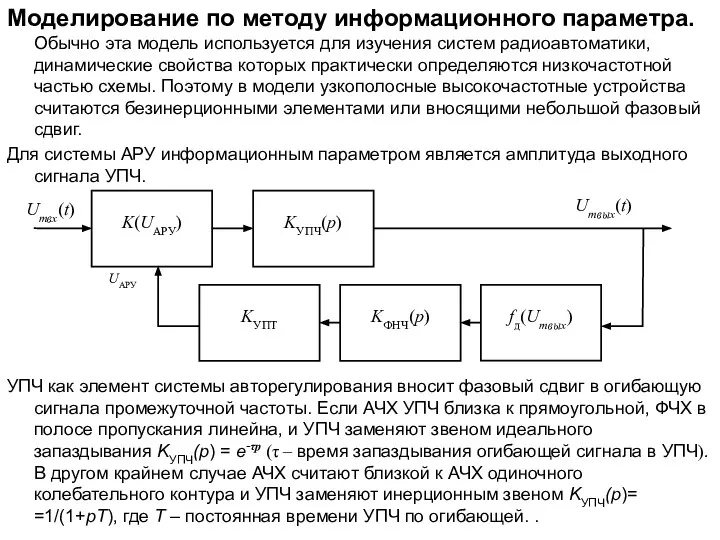 Моделирование по методу информационного параметра
Моделирование по методу информационного параметра Порядок действий в вычислениях
Порядок действий в вычислениях Четырехугольники
Четырехугольники Сечения параллелепипеда
Сечения параллелепипеда Геометрические фигуры
Геометрические фигуры Линейные уравнения. Решение задач с помощью линейных уравнений. 7 класс
Линейные уравнения. Решение задач с помощью линейных уравнений. 7 класс Первообразная. Неопределенный интеграл и его свойства
Первообразная. Неопределенный интеграл и его свойства Признаки равенства треугольников
Признаки равенства треугольников