Содержание
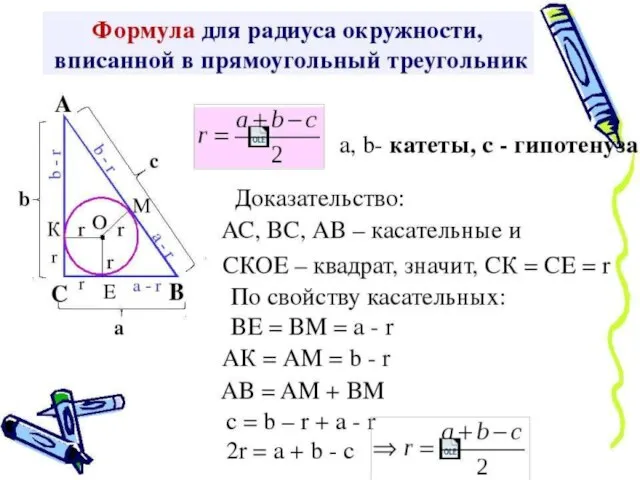
- 3. Задача. В прямоугольный треугольник вписана окружность радиусом 6 м. Периметр треугольника равен 72 м. Найти радиус
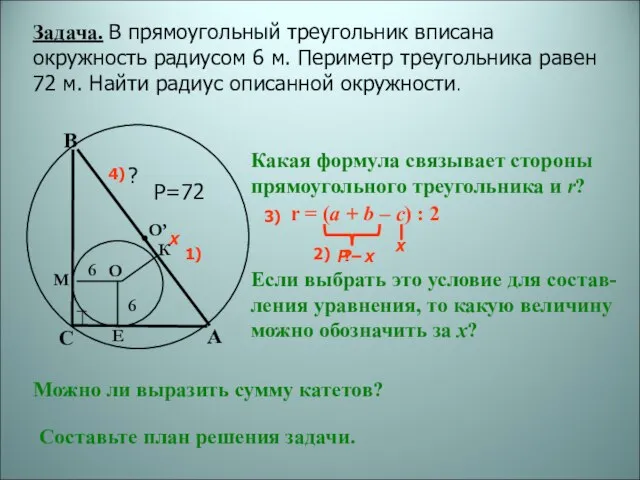
- 4. Задача. В прямоугольный треугольник вписана окружность радиусом 6 м. Периметр треугольника равен 72 м. Найти радиус
- 5. 1) Пусть ВА = х, тогда CA + BC = P – х. Задача. В прямоугольный
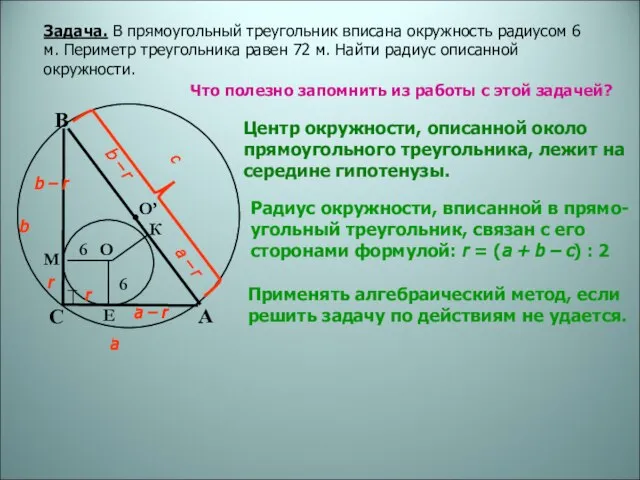
- 6. Задача. В прямоугольный треугольник вписана окружность радиусом 6 м. Периметр треугольника равен 72 м. Найти радиус
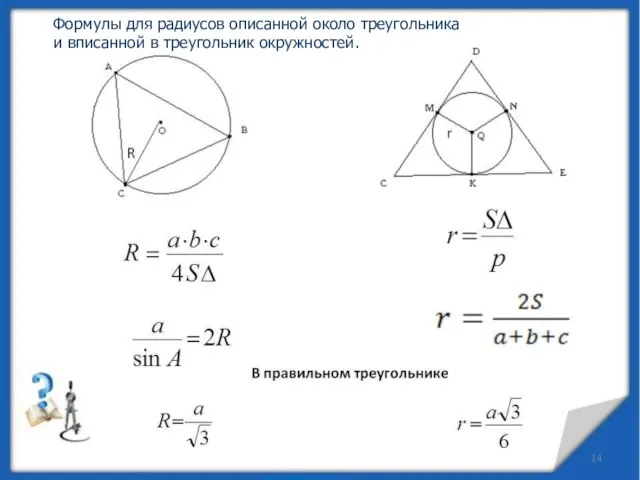
- 7. Формулы для радиусов описанной около треугольника и вписанной в треугольник окружностей.
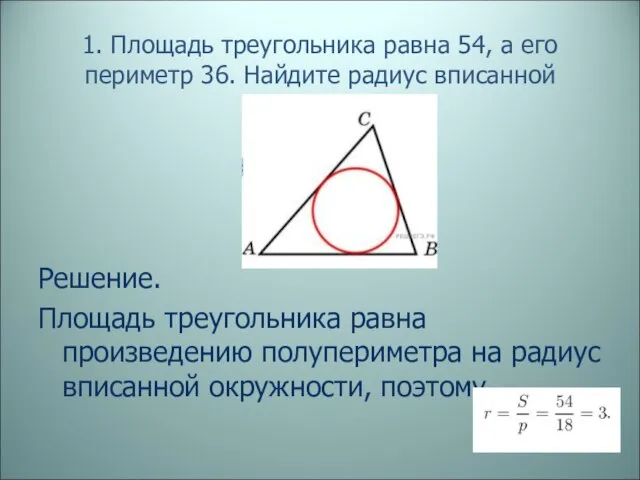
- 8. 1. Площадь треугольника равна 54, а его периметр 36. Найдите радиус вписанной окружности. Решение. Площадь треугольника
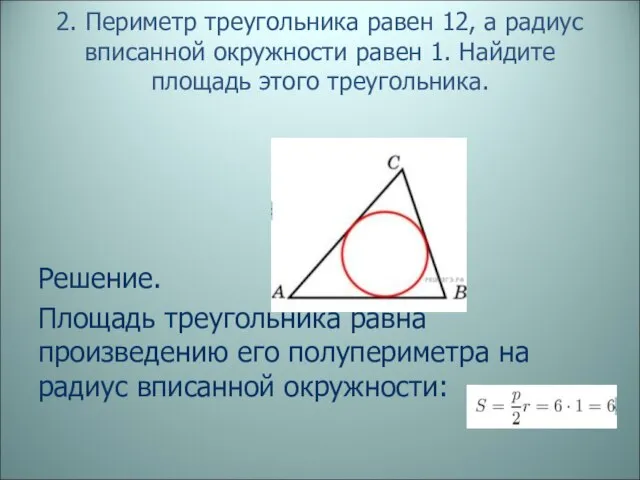
- 9. 2. Периметр треугольника равен 12, а радиус вписанной окружности равен 1. Найдите площадь этого треугольника. Решение.
- 10. Решение задач
- 12. Скачать презентацию



 Задачи на проценты
Задачи на проценты ДЗ №25 стериометрия №5 (1)
ДЗ №25 стериометрия №5 (1) Исследование функции на монотонность и экстремумы
Исследование функции на монотонность и экстремумы деление обыкновенных дробей
деление обыкновенных дробей Задачи на объединение и пересечение множеств
Задачи на объединение и пересечение множеств Перпендикулярные прямые
Перпендикулярные прямые Комбинаторная задача с монетами
Комбинаторная задача с монетами Презентация на тему Упрощение выражений (5 класс)
Презентация на тему Упрощение выражений (5 класс)  Трапеция. Свойства
Трапеция. Свойства Презентация на тему Доли. Обыкновенные дроби (5 класс)
Презентация на тему Доли. Обыкновенные дроби (5 класс)  Неравенство треугольника. 7 класс
Неравенство треугольника. 7 класс Уравнение
Уравнение Математика. Занятие Число 7
Математика. Занятие Число 7 Перпендикулярні площини. Практика 1
Перпендикулярні площини. Практика 1 ИСТОРИЯ СИСТЕМ СЧИСЛЕНИЯ
ИСТОРИЯ СИСТЕМ СЧИСЛЕНИЯ Рациональные числа 6 класс - Презентация по математике_
Рациональные числа 6 класс - Презентация по математике_ Презентация на тему Многочлены
Презентация на тему Многочлены  Бесконечность
Бесконечность Возведение в квадрат суммы и разности двух выражений
Возведение в квадрат суммы и разности двух выражений Редкозубова О.Ф., учитель математики МОУ «СОШ № 138»
Редкозубова О.Ф., учитель математики МОУ «СОШ № 138» Специальная теория относительности
Специальная теория относительности Считалка для ворон Андрея Усачева. Традиционный показ по методике Домана
Считалка для ворон Андрея Усачева. Традиционный показ по методике Домана Книга природы, написанная языком математики
Книга природы, написанная языком математики Натуральные числа. Урок-путешествие в 5-м классе
Натуральные числа. Урок-путешествие в 5-м классе Презентация на тему Итоговый урок: решение систем уравнений
Презентация на тему Итоговый урок: решение систем уравнений  Задания с фигурами
Задания с фигурами Скрещивающиеся прямые
Скрещивающиеся прямые