Содержание
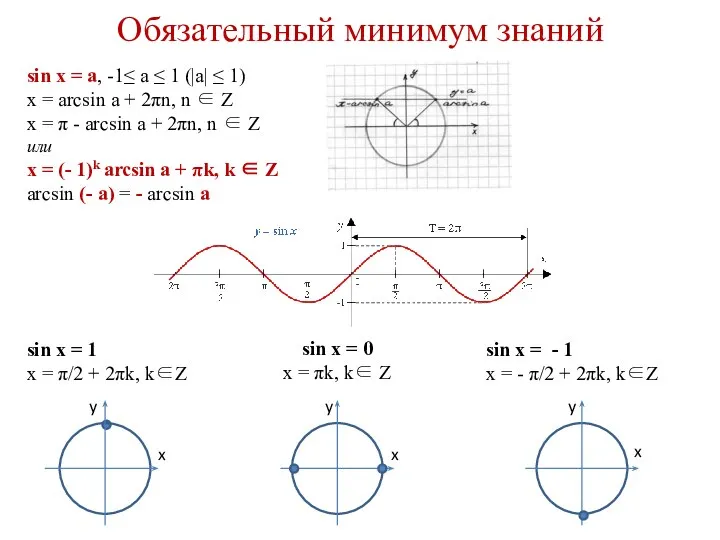
- 2. Обязательный минимум знаний sin x = a, -1≤ a ≤ 1 (|a| ≤ 1) x =
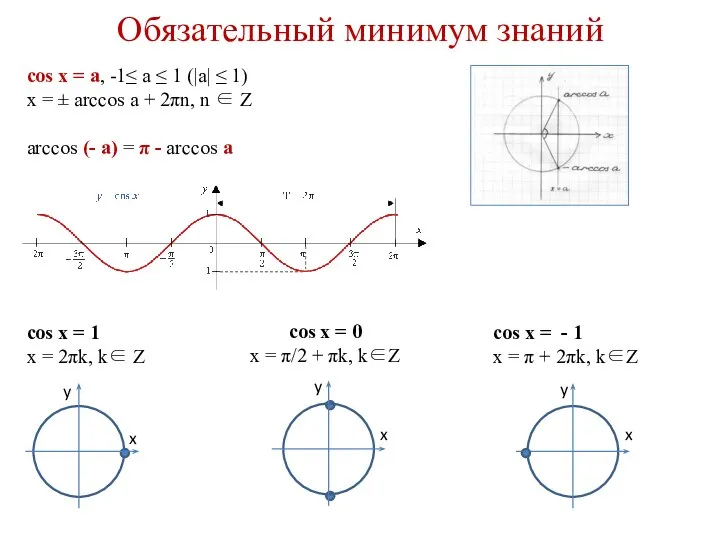
- 3. Обязательный минимум знаний cos x = a, -1≤ a ≤ 1 (|a| ≤ 1) x =
- 4. Обязательный минимум знаний tg x = a, a ∈ R x = arctg a + πn,
- 5. Рекомендации по решению тригонометрических уравнений Свести уравнение к одной функции Свести к одному аргументу Некоторые методы
- 6. Устные упражнения Вычислите arcsin ½ arcsin (- √2/2) arccos √3/2 arccos (-1/2) arctg √3 arctg (-√3/3)
- 7. Различные способы отбора корней cos 2x = ½, x ∈ [- π/2; 3π/2] 2x = ±
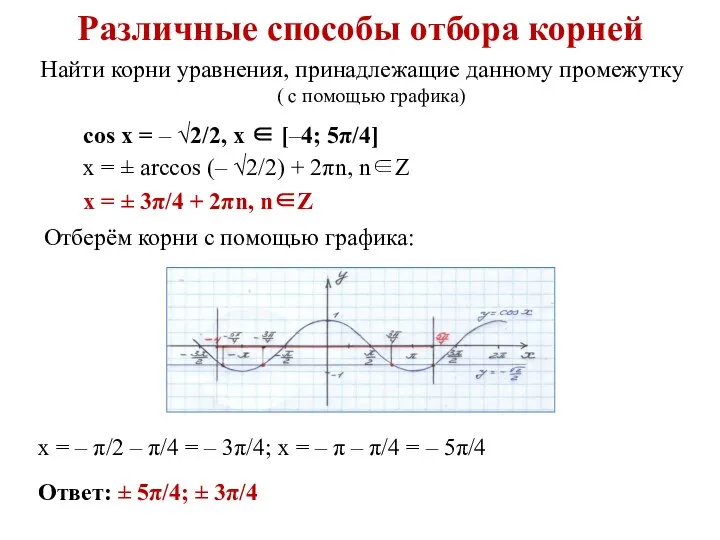
- 8. Различные способы отбора корней Найти корни уравнения, принадлежащие данному промежутку sin 3x = √3/2, x ∈
- 9. Различные способы отбора корней tg 3x = – 1, x ∈ (- π/2; π) 3x =
- 10. Различные способы отбора корней Найти корни уравнения, принадлежащие данному промежутку ( с помощью графика) cos x
- 11. 1. Решить уравнение 72cosx = 49sin2x и указать его корни на отрезке [π; 5π/2] 72cosx =
- 12. 4cos2 x + 8 cos (x – 3π/2) +1 = 0 4cos2x + 8 cos (3π/2
- 13. Проведем отбор корней на отрезке [3π; 9π/2] (с помощью графиков) x = 4π + π/6 =
- 14. 3. Решить уравнение 4 – cos2 2x = 3 sin2 2x + 2 sin 4x Найти
- 15. Проведём отбор корней на отрезке [0; 1] 4 – cos2 2x = 3 sin2 2x +
- 16. 4. Решить уравнение log5(cos x – sin 2x + 25) = 2 Найти его корни на
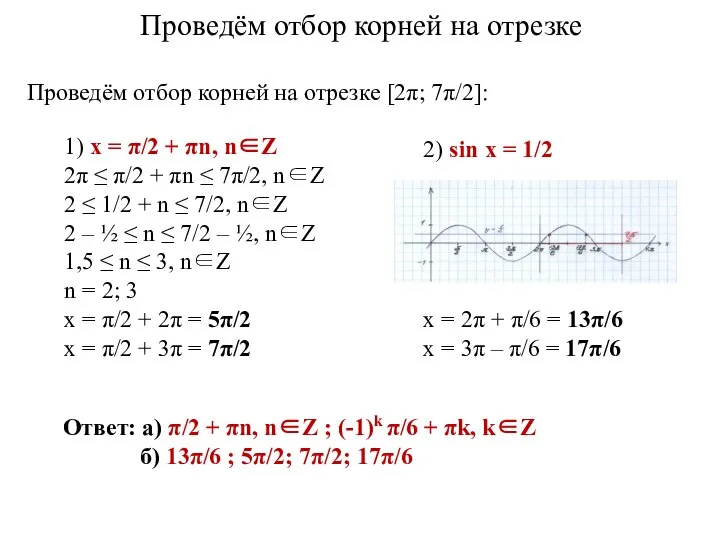
- 17. 1) x = π/2 + πn, n∈Z 2π ≤ π/2 + πn ≤ 7π/2, n∈Z 2
- 18. 5. Решить уравнение 1/sin2x + 1/sin x = 2 Найти его корни на отрезке [-5π/2; -3π/2]
- 19. 1) x = -π/6 + 2πn, n∈Z -5π/2 ≤ -π/6 + 2πn ≤ -3π/2, n∈Z -5/2
- 20. 6. Решить уравнение |sin x|/sin x + 2 = 2cos x Найти его корни на отрезке
- 21. 7. Решить уравнение 4sin3x=3cos(x- π/2) Найти его корни на промежутке [7π/2; 9π/2) Решим уравнение 4sin3x =
- 22. Объединим решения ( см. рисунок) Уравнение можно решить короче, зная формулу sin 3x = 3sinx –
- 23. Проведём отбор корней на промежутке [7π/2; 9π/2) х= πm/3, m∈Z. 7π/2 ≤ πm/3 21/2 ≤ m
- 24. 8. Решить уравнение √1-sin2x= sin x Найти его корни на промежутке [5π/2; 4π] Решим уравнение √1-sin2x=
- 25. Проведём отбор корней на отрезке [5π/2; 4π] x=(-1)k π/4 + πk, k∈Z sin x =√2/2 у
- 26. 9. Решить уравнение (sin2x + 2 sin2x)/√-cos x =0 Найти его корни на промежутке [-5π; -7π/2]
- 27. Отберём корни на заданном отрезке Отберём корни на заданном отрезке [-5π; -7π/2] x= π +2πn, n∈Z
- 28. 10. Решить уравнение 2sin2x =4cos x –sinx+1 Найти его корни на промежутке [π/2; 3π/2] Решим уравнение
- 30. Скачать презентацию








![Проведем отбор корней на отрезке [3π; 9π/2] (с помощью графиков) x =](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1183635/slide-12.jpg)

![Проведём отбор корней на отрезке [0; 1] 4 – cos2 2x =](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1183635/slide-14.jpg)








![Проведём отбор корней на отрезке [5π/2; 4π] x=(-1)k π/4 + πk, k∈Z](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1183635/slide-24.jpg)

![Отберём корни на заданном отрезке Отберём корни на заданном отрезке [-5π; -7π/2]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1183635/slide-26.jpg)

 Вычитание числа 7
Вычитание числа 7 Презентация на тему Наибольший общий делитель (6 класс)
Презентация на тему Наибольший общий делитель (6 класс)  Геометрия. Построение сечений многогранн иков
Геометрия. Построение сечений многогранн иков Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел Занимательная математика
Занимательная математика Чирмешән муниципаль районы Лашман урта гомумбелем бирү мәктәбе
Чирмешән муниципаль районы Лашман урта гомумбелем бирү мәктәбе Теорема Пифагора. Решение задач. Урок для 8 класса
Теорема Пифагора. Решение задач. Урок для 8 класса Формула Бернулли
Формула Бернулли Поворот. Типы вращений
Поворот. Типы вращений Геометрия с Дракошей (2 класс)
Геометрия с Дракошей (2 класс) Назовите углы
Назовите углы Учимся писать цифры
Учимся писать цифры Решение задач
Решение задач Умножение обыкновенных дробей
Умножение обыкновенных дробей Командная олимпиада “Высшая проба” 2019. Разбор задач
Командная олимпиада “Высшая проба” 2019. Разбор задач Презентация на тему ОТРЕЗОК. ДЛИНА ОТРЕЗКА
Презентация на тему ОТРЕЗОК. ДЛИНА ОТРЕЗКА  Числовая последовательность
Числовая последовательность Графический способ решения линейных уравнений с модулями
Графический способ решения линейных уравнений с модулями Презентация на тему Проценты в нашей жизни
Презентация на тему Проценты в нашей жизни  Графическое решение уравнений
Графическое решение уравнений Повторение изученного материала. 1 класс
Повторение изученного материала. 1 класс Величины
Величины Теорема Виета. О свойствах корней
Теорема Виета. О свойствах корней Тетраэдр. Простейший многогранник
Тетраэдр. Простейший многогранник Головоломки. Лабиринты. Магические квадраты
Головоломки. Лабиринты. Магические квадраты Теорема Виета
Теорема Виета Криволинейные интегралы 1 и 2 рода. Связь между криволинейными интегралами 1 и 2 рода, формула Грина. Лекция 28
Криволинейные интегралы 1 и 2 рода. Связь между криволинейными интегралами 1 и 2 рода, формула Грина. Лекция 28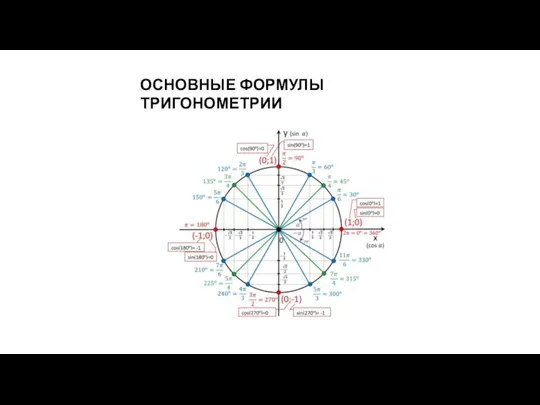 Основные формулы тригонометрии
Основные формулы тригонометрии