Содержание
- 2. Основные задачи математической статистики Описание выборочных данных Оценивание (вероятностное) параметров распределения Проверка статистических гипотез о свойствах
- 3. Основные понятия математической статистики МАТЕМАТИЧЕСКАЯ СТАТИСТИКА — наука о методах обработки экспериментальных данных, полученных при изучении
- 4. Основные понятия математической статистики ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ Х называется функция F(x), определяющая для каждого значения
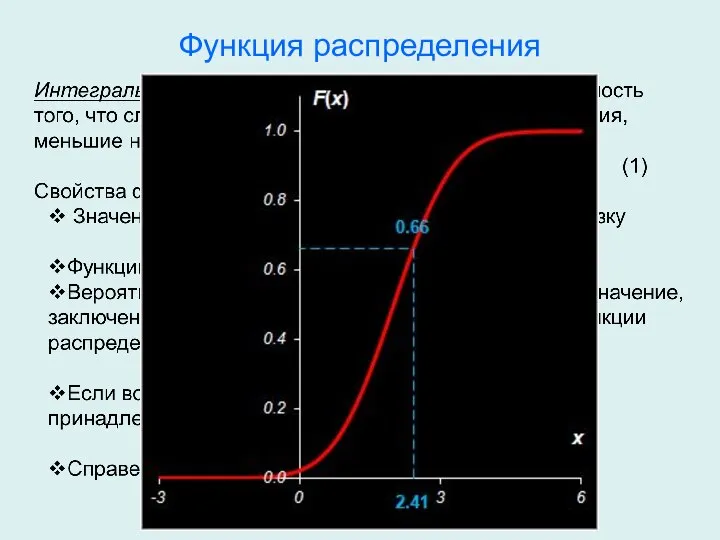
- 5. Функция распределения
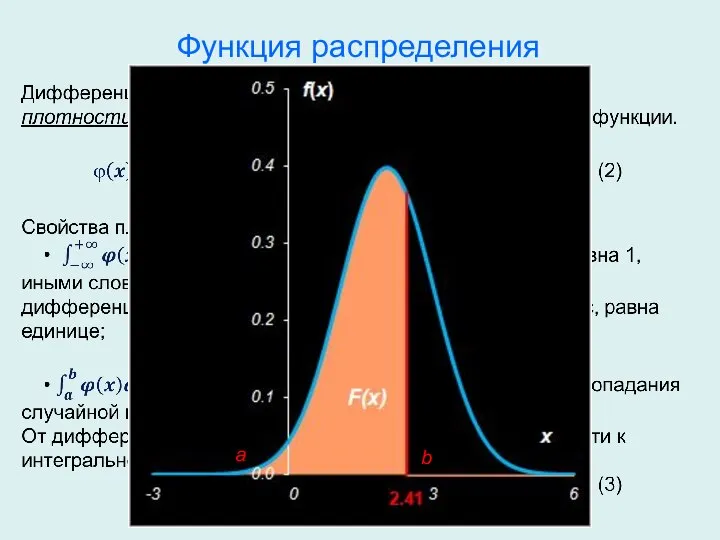
- 6. Функция распределения
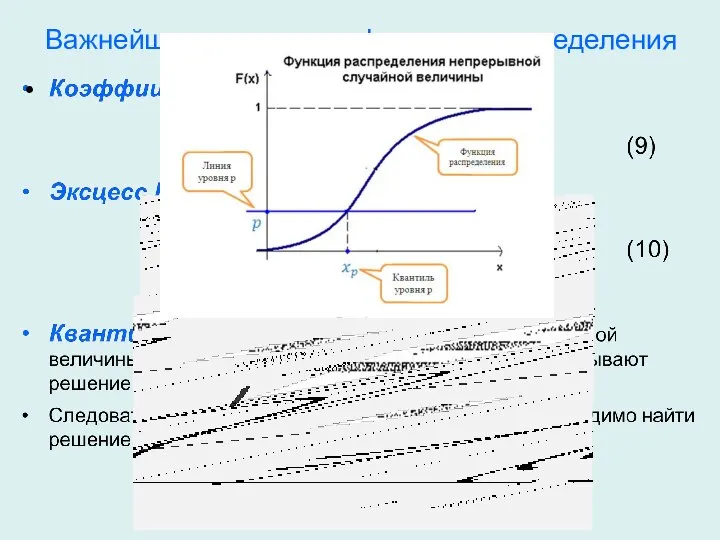
- 7. Важнейшие параметры функции распределения
- 8. Важнейшие параметры функции распределения
- 9. Важнейшие параметры функции распределения
- 10. Оценивание генеральных параметров (свертывание цифровой информации) Требования предъявляемые к оценке параметров распределения (Несмещеность, состоятельность и эффективность):
- 11. Оценивание генеральных параметров (свертывание цифровой информации)
- 12. Оценивание генеральных параметров (свертывание цифровой информации)
- 13. Другие статистические показатели выборок Размах R = xmax – xmin (15) Асимметрия (16) Эксцесс (17)
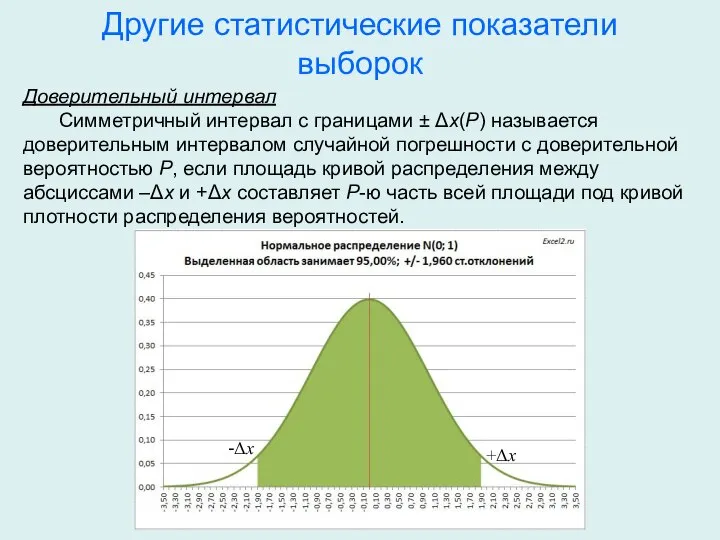
- 14. Другие статистические показатели выборок Доверительный интервал Симметричный интервал с границами ± Δх(Р) называется доверительным интервалом случайной
- 15. Другие статистические показатели выборок
- 16. Теоретические распределения ДИСКРЕТНЫЕ: Биномиальное распределение Распределение Пуассона НЕПРЕРЫВНЫЕ: Нормальное Распределение Стьюдента Логарифмически нормальное Распределение Пирсона Распределение
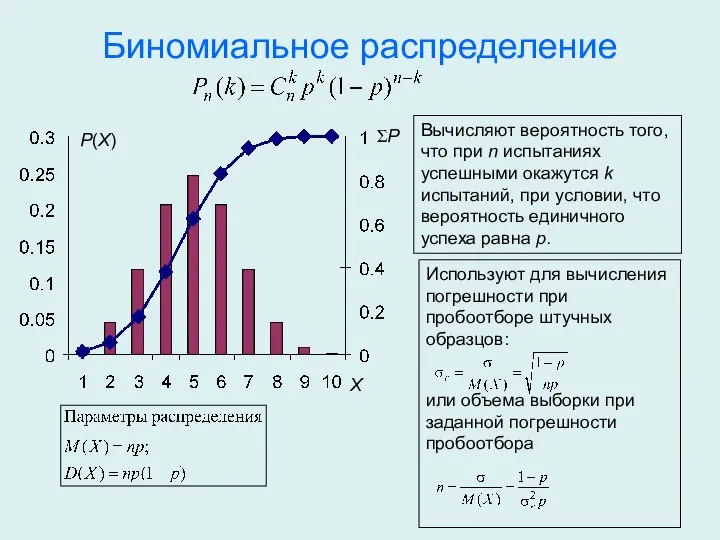
- 17. Используют для вычисления погрешности при пробоотборе штучных образцов: или объема выборки при заданной погрешности пробоотбора Биномиальное
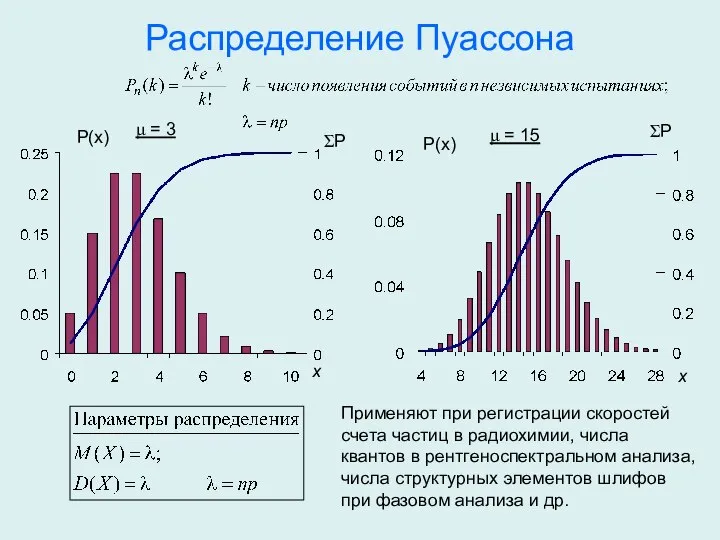
- 18. Распределение Пуассона P(x) P(x) ΣP ΣP Применяют при регистрации скоростей счета частиц в радиохимии, числа квантов
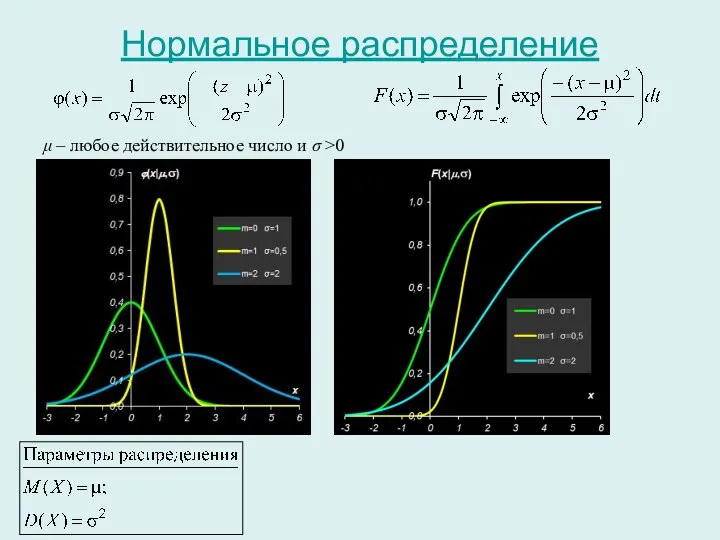
- 19. Нормальное распределение μ – любое действительное число и σ >0
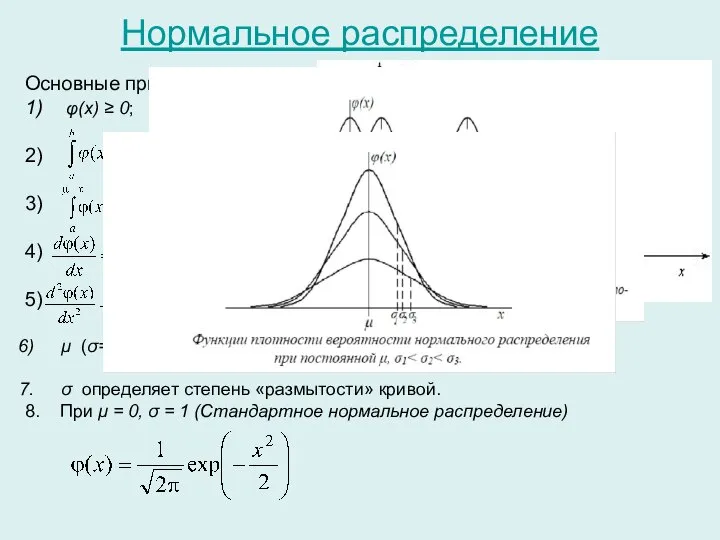
- 20. Нормальное распределение Основные принципы: 1) φ(x) ≥ 0; 2) 3) 4) 5) μ (σ=const) определяет смещение
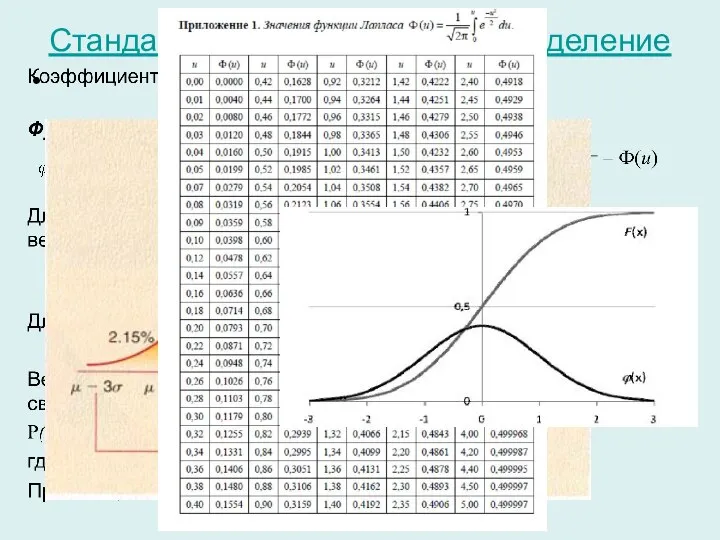
- 21. Стандартное нормальное распределение
- 22. Стандартное нормальное распределение
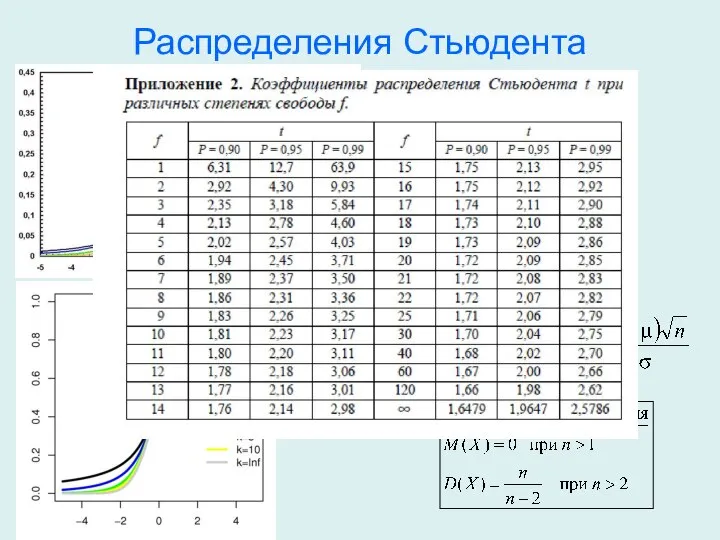
- 23. Распределения Стьюдента
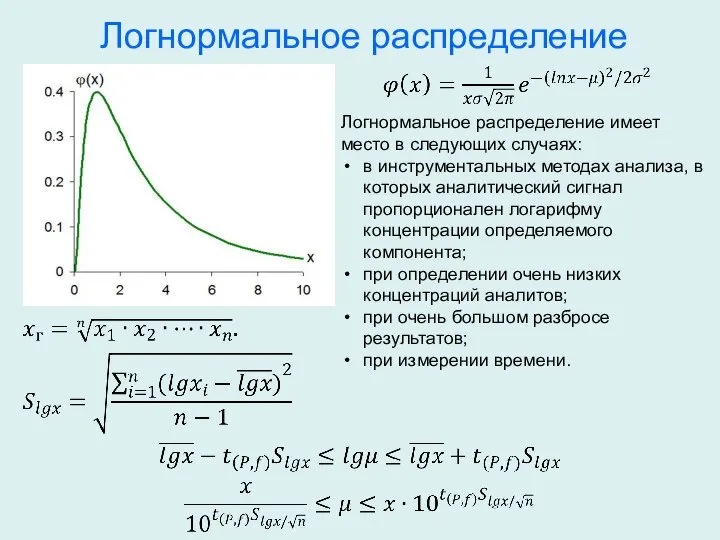
- 24. Логнормальное распределение Логнормальное распределение имеет место в следующих случаях: в инструментальных методах анализа, в которых аналитический
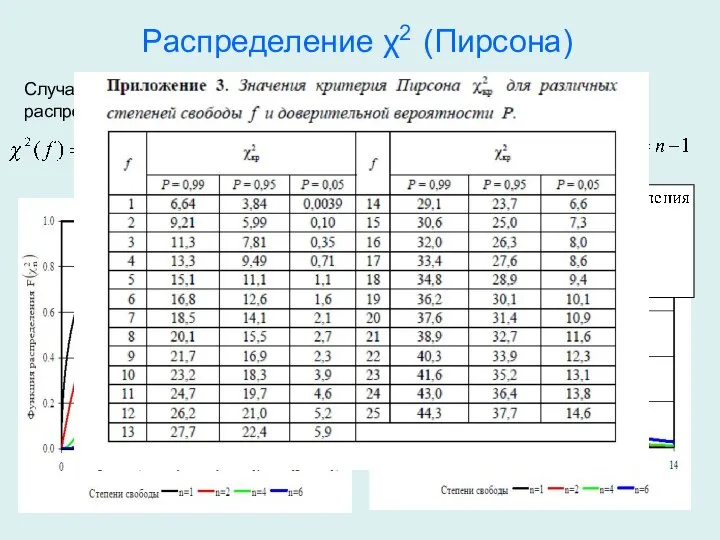
- 25. Распределение χ2 (Пирсона) Случайные величины X1, X2,..., Xn независимые стандартные нормально распределенные величины, т.е. M(X) =
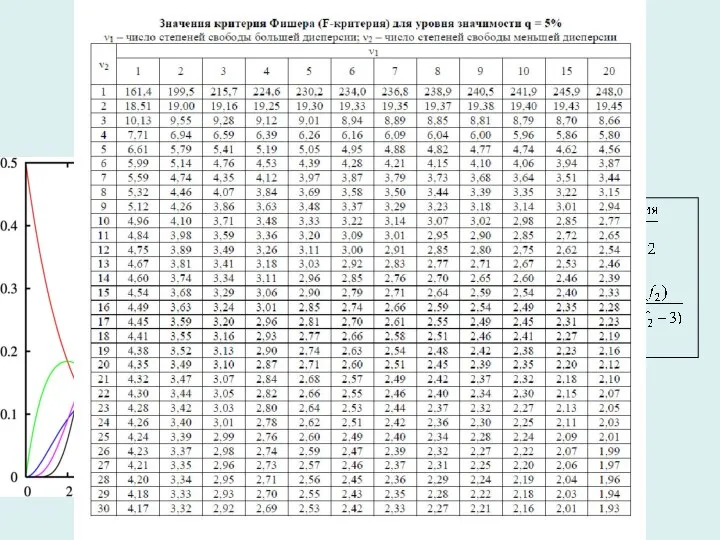
- 26. Распределение Фишера f=5
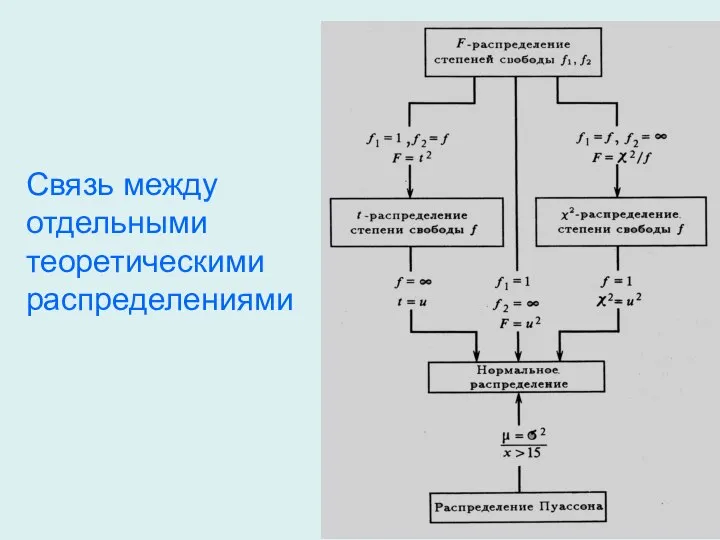
- 27. Связь между отдельными теоретическими распределениями
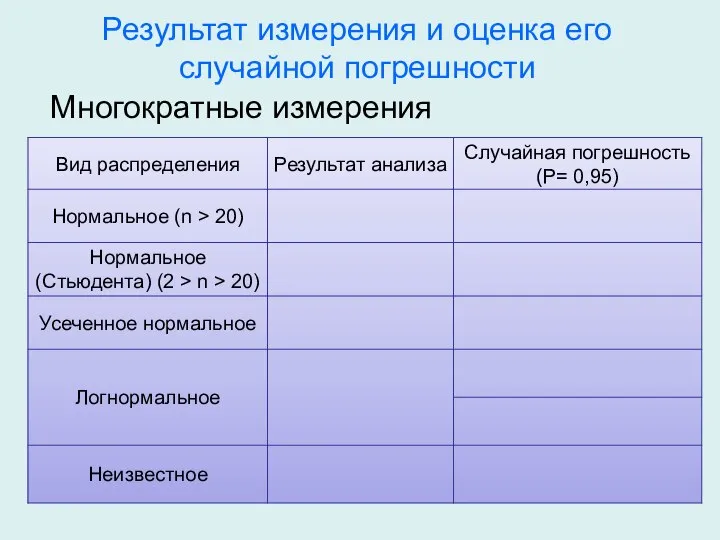
- 28. Результат измерения и оценка его случайной погрешности
- 29. Результат измерения и оценка его случайной погрешности Многократные измерения
- 31. Скачать презентацию













 Теорема Пифагора
Теорема Пифагора Классы интегрируемых функций
Классы интегрируемых функций Интеллектуальная игра по математике для 8 класса
Интеллектуальная игра по математике для 8 класса Движение в геометрии
Движение в геометрии Математическая модель
Математическая модель Примеры. Карточки, счет +-10, 11, 12
Примеры. Карточки, счет +-10, 11, 12 Анализ уравнения на соответствие графику
Анализ уравнения на соответствие графику Масса предметов
Масса предметов Теория игр
Теория игр Методика изучения площади
Методика изучения площади Элементы комбинаторики. Перестановки
Элементы комбинаторики. Перестановки Линейная зависимость и линейная независимость системы векторов. Семинар 4
Линейная зависимость и линейная независимость системы векторов. Семинар 4 Осевая семетрия
Осевая семетрия Координатная плоскость. Ордината. Абсцисса
Координатная плоскость. Ордината. Абсцисса Алгоритм и письменное деление на двузначное число
Алгоритм и письменное деление на двузначное число Темір жолдың жылжымалы құрамын пайдалану, жөндеу және техникалық қызмет көрсету (түрлері бойынша)
Темір жолдың жылжымалы құрамын пайдалану, жөндеу және техникалық қызмет көрсету (түрлері бойынша)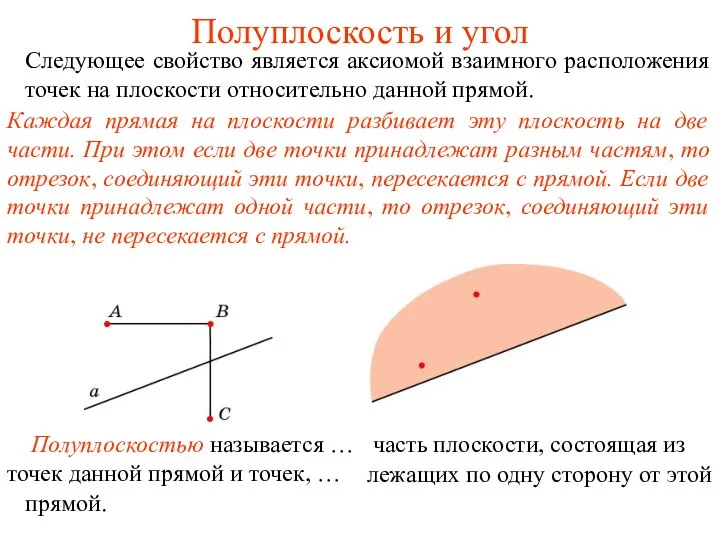 Полуплоскость и угол
Полуплоскость и угол Компланарны ли тройки векторов
Компланарны ли тройки векторов Четырехугольники
Четырехугольники Общее уравнение прямой и плоскости. Лекция1 (1)
Общее уравнение прямой и плоскости. Лекция1 (1) Математика интелектуальная разминка
Математика интелектуальная разминка Усеченый конус
Усеченый конус Кратчайшие расстояния
Кратчайшие расстояния Параллельные прямые 7 класс
Параллельные прямые 7 класс Таблица истинности
Таблица истинности Готфрид Лейбниц (1646 – 1716) – немецкий математик, физик, философ, юрист, языковед
Готфрид Лейбниц (1646 – 1716) – немецкий математик, физик, философ, юрист, языковед Таблицы данных с двумя переменными
Таблицы данных с двумя переменными Показательные уравнения и неравенства
Показательные уравнения и неравенства