Слайд 2
Предельные теоремы теории вероятностей устанавливают зависимость между теоретическими и экспериментальными характеристиками

случайных величин при большом числе испытаний. Изучение закономерностей, проявляющихся в массовых случайных явлениях, позволяет научно предсказывать результаты будущих испытаний.
Предельные теоремы теории вероятностей делятся на две группы, одна из которых получила название закона больших чисел, а другая — центральные предельные теоремы.
Слайд 4 Сущность закона больших чисел

Слайд 5 Первое неравенство Чебышева

Слайд 6 Первое неравенство Чебышева ПРИМЕР 1

Слайд 7 Первое неравенство Чебышева ПРИМЕР 2

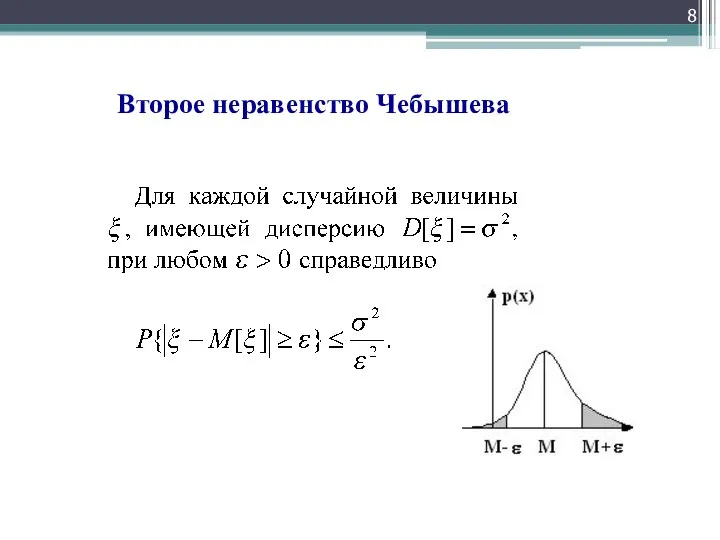
Слайд 8 Второе неравенство Чебышева
Слайд 9 Второе неравенство Чебышева ПРИМЕР

Слайд 11 Доказательство теоремы Чебышева

Слайд 13
Практическое значение теоремы Чебышева.
ПРИМЕР 1.

Слайд 14
Практическое значение теоремы Чебышева.
ПРИМЕР 2.

Слайд 19Центральные предельные теоремы (Ц.П.Т.)
Ц.П.Т.— класс теорем в теории вероятностей, утверждающих, что сумма

достаточно большого количества слабо зависимых случайных величин, имеющих примерно одинаковые масштабы (ни одно из слагаемых не доминирует, не вносит в сумму определяющего вклада), имеет распределение, близкое к нормальному
Слайд 20
Практическое значение Ц.П.Т.
ПРИМЕР.

























 Производная элементарных функций
Производная элементарных функций Презентация на тему Показательная функция
Презентация на тему Показательная функция  Теория о трех перпендикулярах
Теория о трех перпендикулярах Путешествие по реке Математическая. Игра
Путешествие по реке Математическая. Игра Криволинейные интегралы. Теория поля
Криволинейные интегралы. Теория поля Презентация на тему Теорема Пифагора и её применение
Презентация на тему Теорема Пифагора и её применение  Кривые второго порядка
Кривые второго порядка Переменные. Арифметические операции
Переменные. Арифметические операции Организация работы учителя с обучающимися, испытывающими трудности в обучении математике на уровне основного общего образования
Организация работы учителя с обучающимися, испытывающими трудности в обучении математике на уровне основного общего образования Доли. Обыкновенные дроби
Доли. Обыкновенные дроби Презентация на тему Упрощение выражений (6 класс)
Презентация на тему Упрощение выражений (6 класс)  Презентация на тему Вычисление объемов пространственных тел
Презентация на тему Вычисление объемов пространственных тел  Внесение множителя под знак корня. Вынесение множителя из-под знака корня
Внесение множителя под знак корня. Вынесение множителя из-под знака корня Контрольная работа по математике. 8 класс
Контрольная работа по математике. 8 класс Алгоритм сложения и вычитания двузначных чисел 32 + 45, 77 – 32
Алгоритм сложения и вычитания двузначных чисел 32 + 45, 77 – 32 Прямой счет, обратный счет. Повторение
Прямой счет, обратный счет. Повторение Алгоритм решения комбинаторных задач
Алгоритм решения комбинаторных задач Решение систем неравенств с одной переменной
Решение систем неравенств с одной переменной Многокутники. Види многокутників
Многокутники. Види многокутників Площадь параллелограмма
Площадь параллелограмма Ускоренное умножение
Ускоренное умножение Статистические оценки параметров распределения. Точечные и интервальные оценки
Статистические оценки параметров распределения. Точечные и интервальные оценки Методы решения экстремальных задач
Методы решения экстремальных задач Логарифмические выражения
Логарифмические выражения Симметрия в пространстве
Симметрия в пространстве Вычитание чисел с переходом через десяток в пределах 20. Тренажёр
Вычитание чисел с переходом через десяток в пределах 20. Тренажёр Координатная плоскость (урок 3)
Координатная плоскость (урок 3) Свойства степеней
Свойства степеней