итерационными методами, в которых последовательно, шаг за шагом, производится уточнение начального приближения корня. Итерацией называется совокупность вычислительных операций, приводящих к новому приближенному значению корня. Если каждое последующее значение x(k) (k=1,2,3,…) находится все ближе к точному значению, говорят, что метод сходится. В противном случае метод расходится. Для реализации итерационного процесса должны быть заданы начальное приближение x(0) и точность ε, с которой найти решение уравнения. Условие окончание имеет вид: |x(k)-x(k-1)| ≤·ε.Все методы можно разделить на две группы: с условной и безусловной сходимостью.
Метод половинного деления
В этом методе на каждой итерации новое приближение определяется как:
x(k)=(a(k-1)+b(k-1))/2, где к – номер итерации.
Алгоритм
Задаем функцию f(x), отрезок [a(0),b(0)], точность ε и k=1.
Вычисляем приближение x(k)=(a(k-1)+b(k-1))/2
Определяем новый отрезок [a(k),b(k)]. Проверяем, если f(a(k-1))*f(x(k))>0, то a(k)=x(k) и b(k)=b(k-1), иначе a(k)=a(k-1) и b(k)=x(k).
Проверяем условие окончания, если |b(k)-a(k)| ≤·2ε, то за ответ принимаем значение равное x=(a(k)+b(k))/2 и переходим на пункт 5, иначе k=k+1 и переходим на пункт 2.
выводим x и f(x).
Методы с безусловной сходимостью
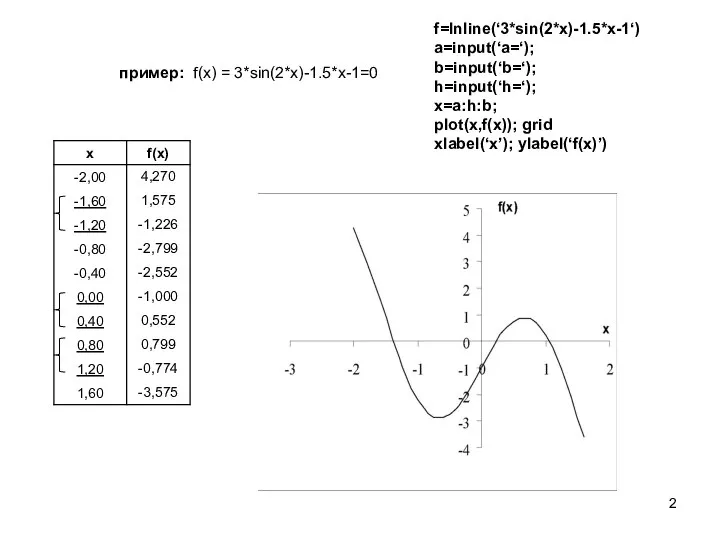
![Уточнение корня на отрезке [a,b], в котором локализован только один корень, осуществляется](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/935078/slide-2.jpg)



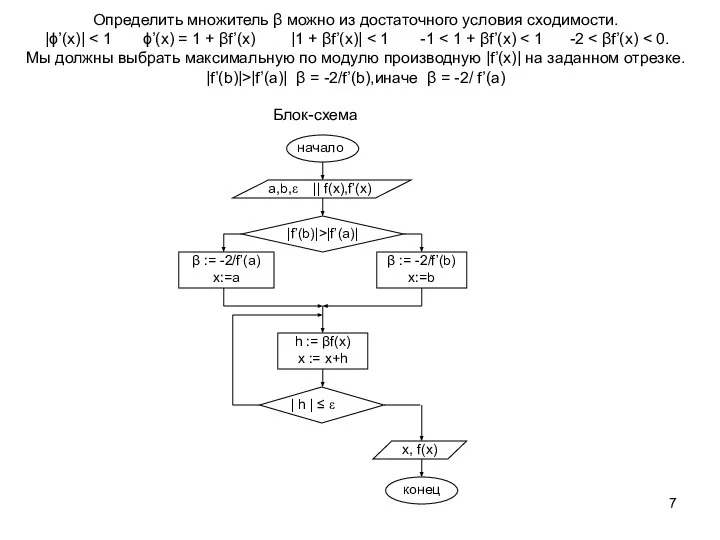
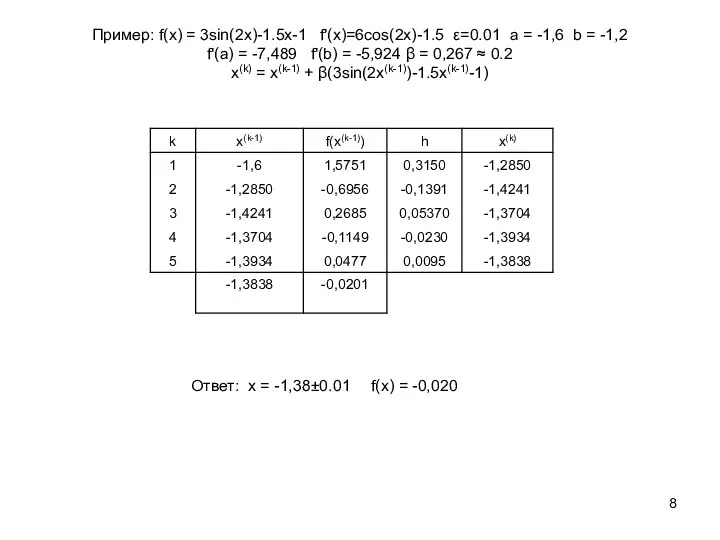

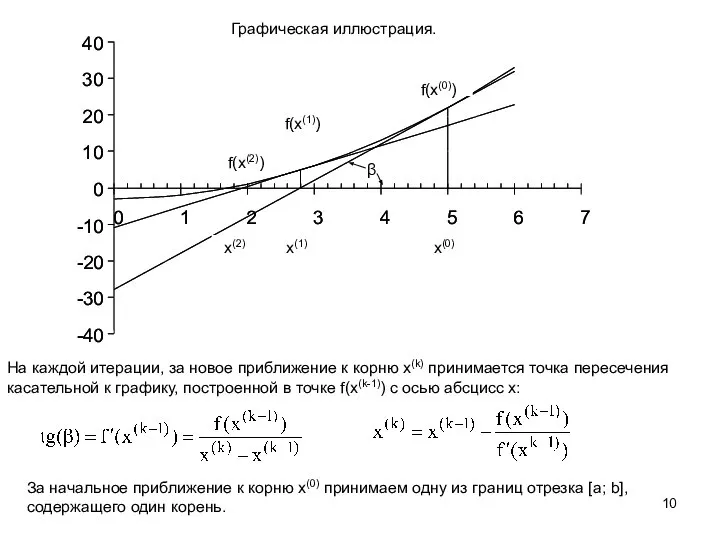
![алгоритм Задаем функцию f(x) отрезок [a;b] и точность ε. За начальное приближение](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/935078/slide-10.jpg)
 Правила вычисления производных
Правила вычисления производных Задачи. Геометрия 8 кл
Задачи. Геометрия 8 кл ЕГЭ. Экономические задачи IV
ЕГЭ. Экономические задачи IV Построение сечений
Построение сечений Параллельные прямые. Признак параллельности прямых по равенству накрест лежащих углов
Параллельные прямые. Признак параллельности прямых по равенству накрест лежащих углов Сложение вида +2 +3 с переходом через десяток
Сложение вида +2 +3 с переходом через десяток Старинные задачи на дроби
Старинные задачи на дроби Презентация на тему Что такое функция? 7 класс
Презентация на тему Что такое функция? 7 класс  Правильные многогранник. Повторение
Правильные многогранник. Повторение Подготовка к дифференцированному зачёту по математике. Нижегородский авиационный технический колледж
Подготовка к дифференцированному зачёту по математике. Нижегородский авиационный технический колледж Степени и логарифмы
Степени и логарифмы Метод неопределенных коэффициентов. Теорема о рациональном корне многочлена с целыми коэффициентами
Метод неопределенных коэффициентов. Теорема о рациональном корне многочлена с целыми коэффициентами Арифметическая и геометрическая прогрессии
Арифметическая и геометрическая прогрессии Сантиметр - единица измерения длины
Сантиметр - единица измерения длины Вычитание. Решение текстовых задач с помощью сложения и вычитания
Вычитание. Решение текстовых задач с помощью сложения и вычитания Занимательная геометрия (1 класс)
Занимательная геометрия (1 класс) Исследование на принадлежность классам функцию. Практическая работа
Исследование на принадлежность классам функцию. Практическая работа Перпендикулярные прямые
Перпендикулярные прямые Обратные тригонометрические функции
Обратные тригонометрические функции Случайные величины 14 сен
Случайные величины 14 сен Корреляционно-регрессионный анализ
Корреляционно-регрессионный анализ Повторение и закрепление. Итоговое повторение за год. 4 класс
Повторение и закрепление. Итоговое повторение за год. 4 класс Решаем практическую задачу
Решаем практическую задачу Загадки и тайны треугольника
Загадки и тайны треугольника Параллелограмм
Параллелограмм Признаки параллельности прямых
Признаки параллельности прямых Геометрический материал
Геометрический материал Множества точек на координатной плоскости, расстояние между точками координатной прямой
Множества точек на координатной плоскости, расстояние между точками координатной прямой