Содержание
- 2. 1) Дано: точки А,В,С,Д не принадлежат одной плоскости. Доказать: любые три точки являются вершинами треугольника.
- 3. Метод от противного Предположим, что три точки А, В и С не являются вершинами треугольника, т.е.
- 4. 2)
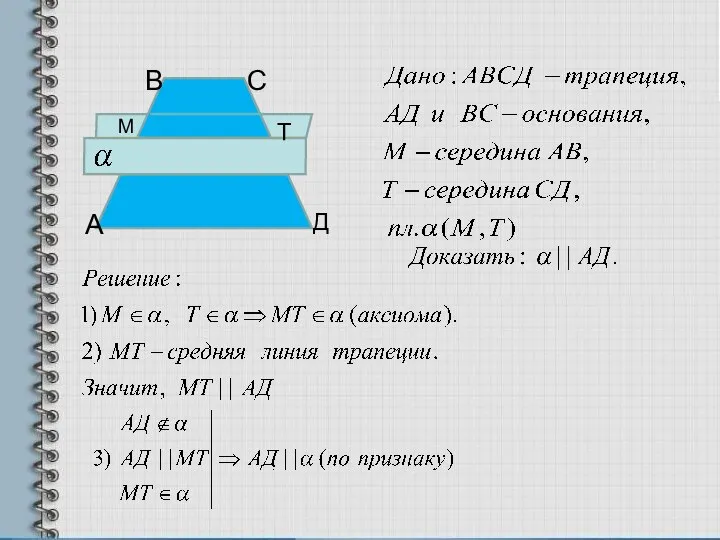
- 5. 3). Дана трапеция АВСД с основаниями АД и ВС. Через середины боковых сторон проведена плоскость .
- 6. М А В С Д Т
- 8. Скачать презентацию




 Операции, функции, выражения
Операции, функции, выражения В мире процентов
В мире процентов Теорема Пифагора
Теорема Пифагора Чтение девятизначных чисел
Чтение девятизначных чисел Признак существования определенного интеграла. Лекция №7
Признак существования определенного интеграла. Лекция №7 Луч – это отрезок. Ломаная состоит из звеньев
Луч – это отрезок. Ломаная состоит из звеньев Геометрическое путешествие. Дни математики в начальной школе (10.01.2019-31.01.2019) ГБОУ Школа № 170 им. А.П. Чехова
Геометрическое путешествие. Дни математики в начальной школе (10.01.2019-31.01.2019) ГБОУ Школа № 170 им. А.П. Чехова Дифференциальные уравнения. Лекция 3. Простейшие дифференциальные уравнения
Дифференциальные уравнения. Лекция 3. Простейшие дифференциальные уравнения Величины. Масса (1 класс)
Величины. Масса (1 класс) Презентация на тему Деловая игра по математике
Презентация на тему Деловая игра по математике  Учим состав чисел с Колобком
Учим состав чисел с Колобком Графический способ решения систем уравнений. Свойства графиков функций
Графический способ решения систем уравнений. Свойства графиков функций Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии
Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии Решение задач. Параллельные прямые
Решение задач. Параллельные прямые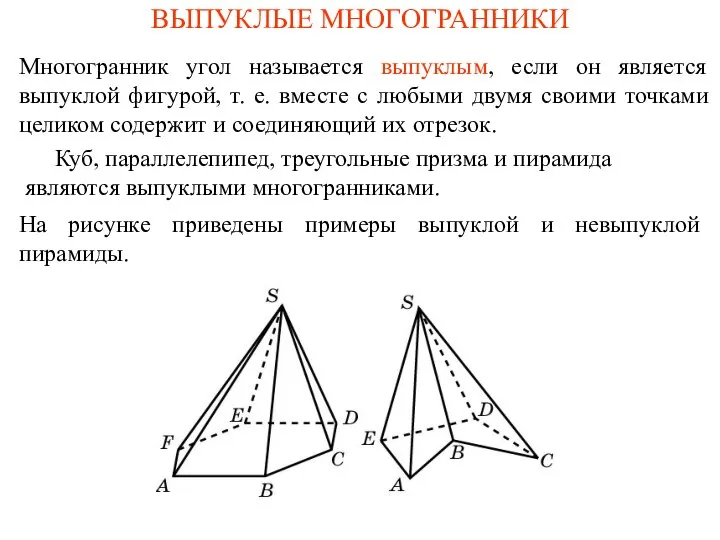 Выпуклые многогранники
Выпуклые многогранники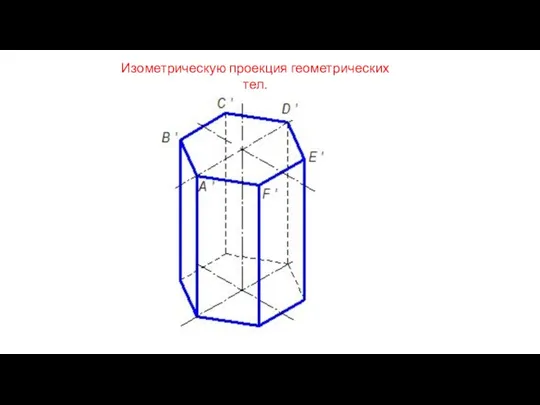 Шестигранная призма в изометрии
Шестигранная призма в изометрии Четырехугольники. Свойства четырехугольников. Решение задач
Четырехугольники. Свойства четырехугольников. Решение задач Распределение случайных величин. Функция распределения и плотность распределения случайной величины
Распределение случайных величин. Функция распределения и плотность распределения случайной величины Множества
Множества Урок 23
Урок 23 Правильные многогранники в представлении пяти стихий
Правильные многогранники в представлении пяти стихий Формулы. Урок 1
Формулы. Урок 1 Тригонометрия. Итоговое повторение
Тригонометрия. Итоговое повторение Презентация на тему Комбинаторные задачи
Презентация на тему Комбинаторные задачи  В четырех углах или Путешествие в семью параллелограммов
В четырех углах или Путешествие в семью параллелограммов Арифметические операции над матрицами
Арифметические операции над матрицами Задачи в координатах
Задачи в координатах Решение систем линейных уравнений при помощи компьютерных технологий
Решение систем линейных уравнений при помощи компьютерных технологий