Содержание
- 2. - Что называется отношением двух отрезков? - В каком случае говорят, что отрезки AB и CD
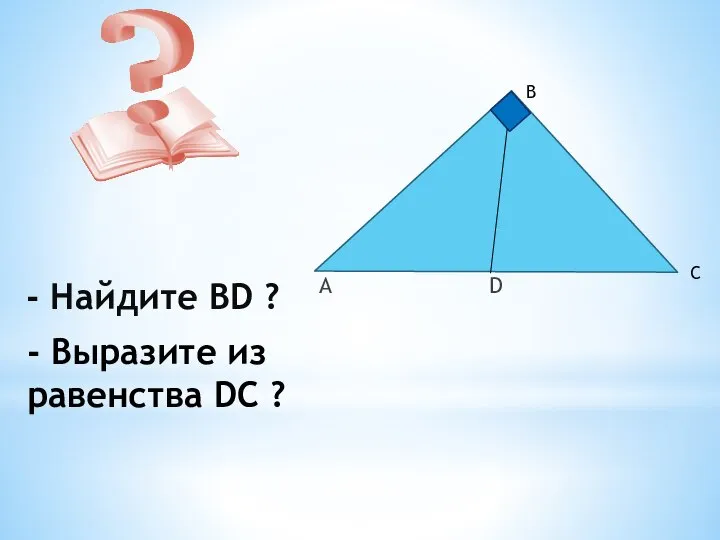
- 3. - Найдите BD ? A D - Выразите из равенства DC ? B C
- 4. - Постройте угол равный данному - Постройте медиану AM ΔABC -Постройте прямую, параллельную стороне AB ΔABC
- 5. -В чем заключается метод построения фигур методом подобия? - Сколько и какие этапы включают в себя
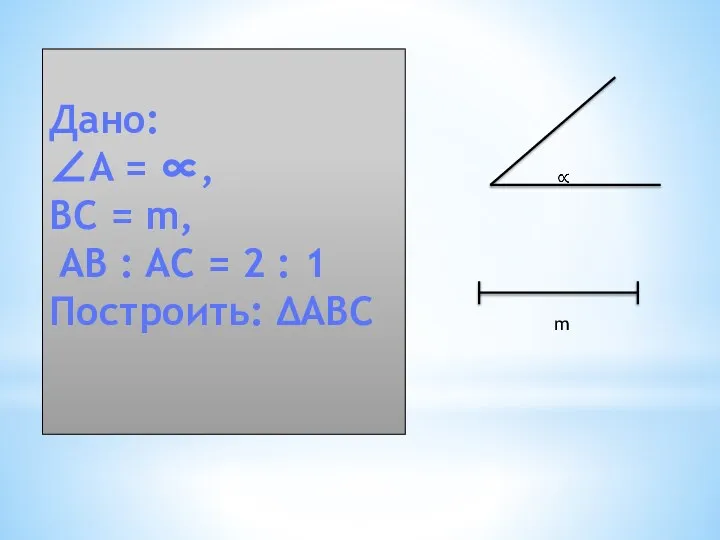
- 6. Задача 1. Построить треугольник ABC по углу A,отношению сторон AB : AC = 2 : 1
- 7. m
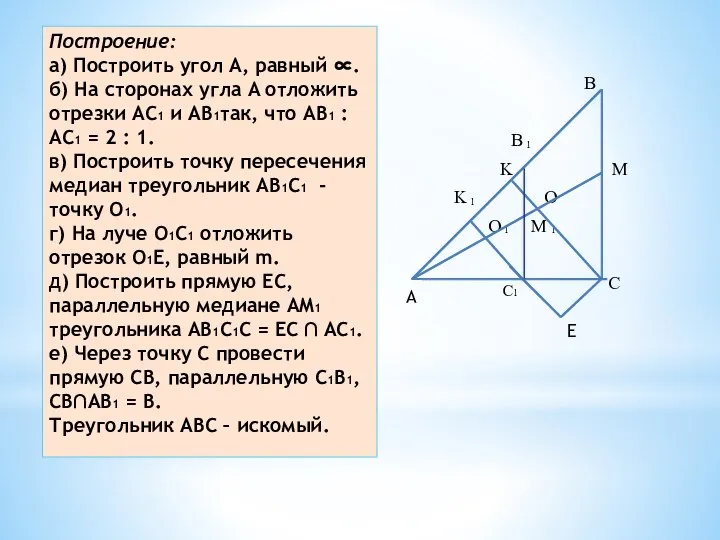
- 8. Построение: а) Построить угол A, равный ∝. б) На сторонах угла A отложить отрезки AC1 и
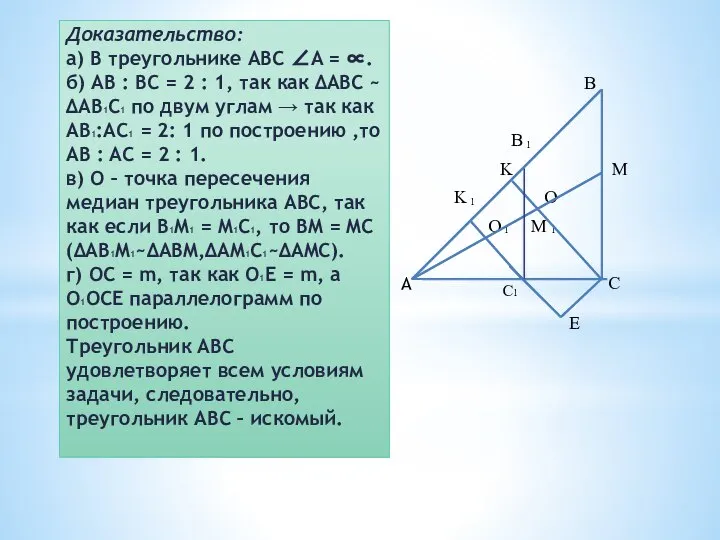
- 9. Доказательство: а) В треугольнике ABC ∠A = ∝. б) AB : BC = 2 : 1,
- 10. Задача 2 (№ 588) Постройте треугольник ABC по углу A и медиане AM, если известно, что
- 11. Дано: ∠A = ∝, AM = m, AB : AC = 2 : 3. Построить: ΔABC
- 12. Построение: а) Построить ∠A = ∝ б) На одной из сторон угла A отложить 2 одинаковых
- 13. Доказательство: а) ΔANF ~ΔABC, (∠A – общий ,∠ABC = ∠ANF при NF || BC и секущей
- 14. Задача 3 (№589) Постройте треугольник ABC по углу A и стороне BC, если известно, что AB
- 15. Дано: ∠A = ∝, BC = m, AB : AC = 2 : 1 Построить: ΔABC
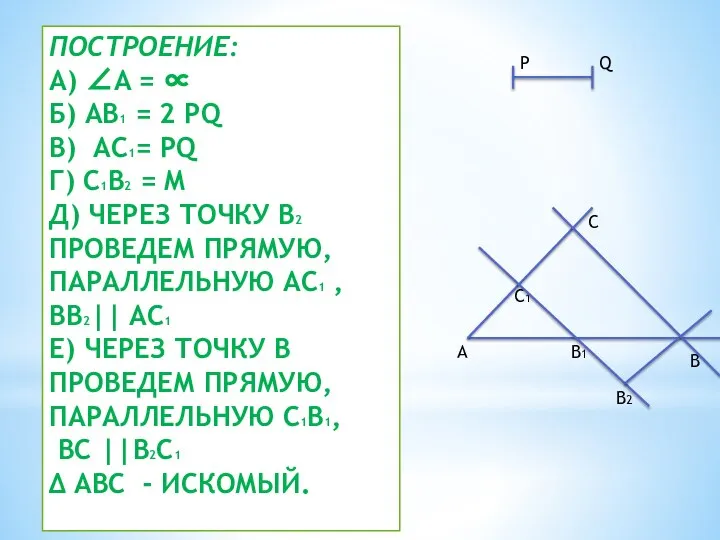
- 16. ПОСТРОЕНИЕ: А) ∠A = ∝ Б) AB1 = 2 PQ В) AC1= PQ Г) C1B2 =
- 17. A B1 C1 B2 B C
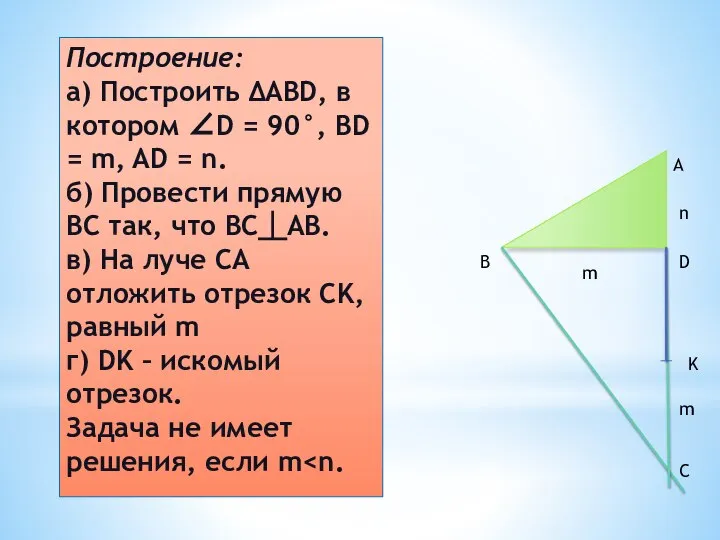
- 18. Задача 4.
- 20. Построение: а) Построить ΔABD, в котором ∠D = 90°, BD = m, AD = n. б)
- 22. Скачать презентацию












 Определенный интеграл
Определенный интеграл Теорема. Франсуа Виет (1540-1603)
Теорема. Франсуа Виет (1540-1603) Координатная плоскость
Координатная плоскость Pakāpes vingrinājumi (bez atb)
Pakāpes vingrinājumi (bez atb) Вычисление неопределенных интегралов методом интегрирования по частям
Вычисление неопределенных интегралов методом интегрирования по частям Степенная функция и её график
Степенная функция и её график Сложение и вычитание положительных десятичных дробей
Сложение и вычитание положительных десятичных дробей Морской бой
Морской бой Правило нахождения первообразной
Правило нахождения первообразной Интерполяция функций
Интерполяция функций Презентация на тему Площадь многоугольников
Презентация на тему Площадь многоугольников  Устный счёт. 3 класс
Устный счёт. 3 класс Разбор заданий очного тура Олимпиады по математике
Разбор заданий очного тура Олимпиады по математике Тригонометрические уравнения
Тригонометрические уравнения Финансовая математика: банки, вклады, кредиты. Часть 2
Финансовая математика: банки, вклады, кредиты. Часть 2 Перестановка слагаемых
Перестановка слагаемых Кратное сравнение
Кратное сравнение Некоторые виды распределений непрерывных случайных величин
Некоторые виды распределений непрерывных случайных величин Чтение графика функций
Чтение графика функций Признаки подобия треугольников. Урок 31
Признаки подобия треугольников. Урок 31 Экстремумы (1)
Экстремумы (1) Презентация на тему Красота и гармония в симметрии
Презентация на тему Красота и гармония в симметрии  Презентация на тему Площадь сферы
Презентация на тему Площадь сферы  Равномерное прямолинейное движение. 9 класс
Равномерное прямолинейное движение. 9 класс Векторная алгебра
Векторная алгебра Современное школьное математическое образование
Современное школьное математическое образование Связь между суммой и слагаемыми (1 класс)
Связь между суммой и слагаемыми (1 класс) Определение знаков коэффициентов K и b в линейной функции по их графикам
Определение знаков коэффициентов K и b в линейной функции по их графикам