Комбинаторика. 11 класс

ВСТАВЬТЕ ПРОПУЩЕННОЕ СЛОВО
______________ из n элементов называется каждое расположение этих элементов в определенном порядке.
______________ из n элементов по k (k ≤ n) называется любое множество, состоящее из k элементов, взятых в определенном порядке из данных n элементов.
__________ из n элементов по k называется любое множество из k элементов, выбранных из n элементов.

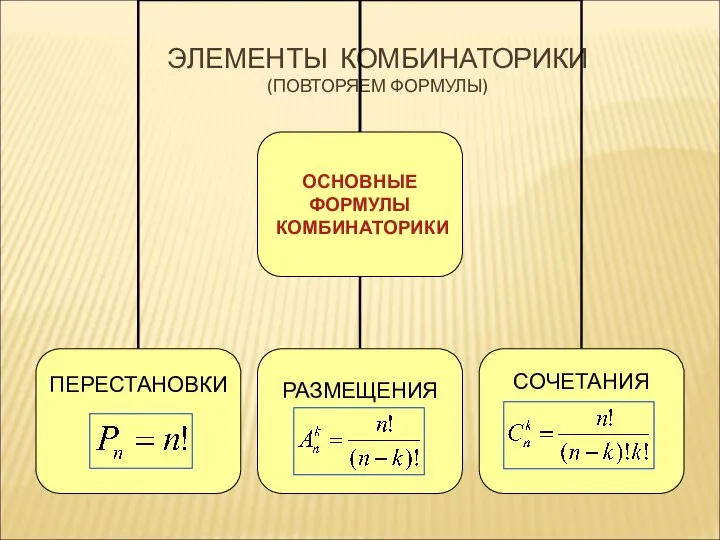
ЭЛЕМЕНТЫ КОМБИНАТОРИКИ
(ПОВТОРЯЕМ ФОРМУЛЫ)

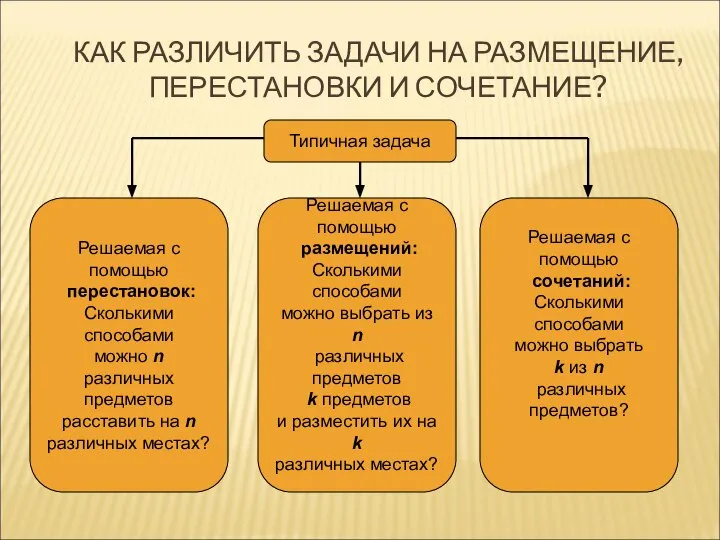
КАК РАЗЛИЧИТЬ ЗАДАЧИ НА РАЗМЕЩЕНИЕ, ПЕРЕСТАНОВКИ И СОЧЕТАНИЕ?
Типичная задача
Решаемая с помощью
перестановок:
Сколькими способами
можно n различных
предметов
расставить на n
различных местах?
Решаемая с помощью
размещений:
Сколькими способами
можно выбрать из n
различных предметов
k предметов
и разместить их на k
различных местах?
Решаемая с помощью
сочетаний:
Сколькими способами
можно выбрать
k из n
различных предметов?

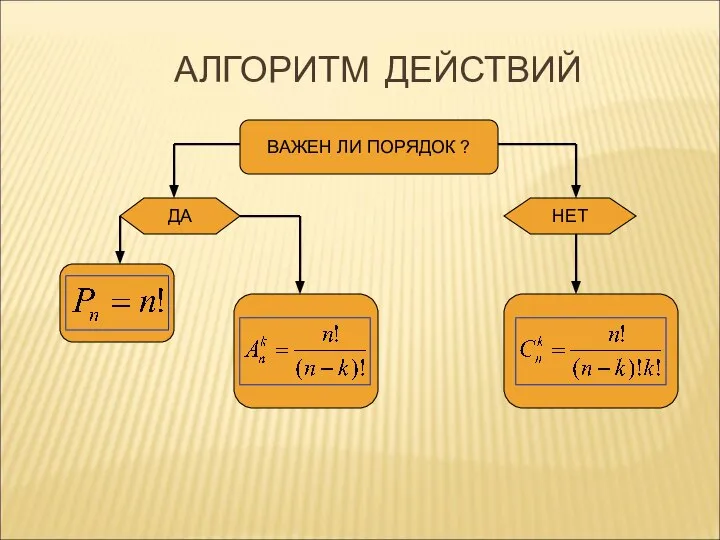
АЛГОРИТМ ДЕЙСТВИЙ
ВАЖЕН ЛИ ПОРЯДОК ?
ДА
НЕТ

ЗАДАЧА № 1.
СКОЛЬКИМИ СПОСОБАМИ МОГУТ ВСТАТЬ В ОЧЕРЕДЬ В БИЛЕТНУЮ КАССУ 5 ЧЕЛОВЕК?
1
2
3
4
6 способов
120 способов
100 способов
50 способов

Решение:
Различные варианты n человек в очереди отличаются один от другого только порядком расположения людей, т.е. являются различными перестановками из n элементов.
Пять человек могут встать в очередь
P5 = 5! = 120 различными способами.
Ответ: 120 способами.
ЗАДАЧА № 1

ЗАДАЧА № 2
СКОЛЬКИМИ СПОСОБАМИ 4 ЧЕЛОВЕКА МОГУТ РАЗМЕСТИТСЯ НА ЧЕТЫРЕХМЕСТНОЙ СКАМЕЙКЕ?
1
2
4
3
4 способами
48 способами
24 способами
16 способами

ЗАДАЧА № 2
Решение:
Количество человек равно количеству мест на скамейке, поэтому количество способов размещения равно числу перестановок из 4 элементов:
Р = 4! = 24
Можно рассуждать по правилу произведения: для первого человека можно выбрать любое из 4 мест, для второго – любое из 3 оставшихся, для третьего – любое из 2 оставшихся, последний займет 1 оставшееся место; всего 4·3·2·1 = 24.
Ответ: 24 способами.

ЗАДАЧА № 3
НАЙДИТЕ СУММУ ЦИФР ВСЕХ ЧЕТЫРЕХЗНАЧНЫХ ЧИСЕЛ, КОТОРЫЕ МОЖНО СОСТАВИТЬ ИЗ ЦИФР 1, 3, 5, 7 (БЕЗ ИХ ПОВТОРЕНИЯ).
1
2
3
4
380
384
105
16

ЗАДАЧА № 3
Решение:
Каждое четырехзначное число, составленное из цифр 1, 3, 5, 7 (без повторения), имеет сумму цифр, равную 1+3+5+7=16.
Из этих цифр можно составить Р4 = 4! = 24 различных числа, отличающихся только порядком цифр.
Сумма цифр всех этих чисел равна
16 х 24 = 384.
Ответ: 384.

ЗАДАЧА № 4
СКОЛЬКО СУЩЕСТВУЕТ СПОСОБОВ ВЫБРАТЬ ТРОИХ РЕБЯТ ИЗ ШЕСТЕРЫХ ЖЕЛАЮЩИХ ДЕЖУРИТЬ ПО СТОЛОВОЙ?
3
2
1
4
6
18
20
720

ЗАДАЧА № 4
Решение:
Количество сочетаний из 6 по 3 (порядок выбора не имеет значения) равно:
Ответ: 20 способов

ЗАДАЧА № 5
В КЛАССЕ 9 ЧЕЛОВЕК УСПЕШНО ЗАНИМАЮТСЯ МАТЕМАТИКОЙ. СКОЛЬКИМИ СПОСОБАМИ МОЖНО ВЫБРАТЬ ИЗ НИХ ДВОИХ УЧАЩИХСЯ ДЛЯ УЧАСТИЯ В МАТЕМАТИЧЕСКОЙ ОЛИМПИАДЕ?
1
2
3
4
2
36
81
18

ЗАДАЧА № 5
Решение:
Выбираем двух учащихся из 9, порядок выбора не имеет значения (оба выбранных пойдут на олимпиаду как равноправные); количество способов выбора равно числу сочетаний из 9 по 2:
Ответ: 36 способов

ЗАДАЧА № 6
В КЛАССЕ УЧАТСЯ 18 МАЛЬЧИКОВ И 14 ДЕВОЧЕК. ДЛЯ УБОРКИ ТЕРРИТОРИИ ШКОЛЫ ТРЕБУЕТСЯ ВЫДЕЛИТЬ ЧЕТЫРЕХ МАЛЬЧИКОВ И ТРЕХ ДЕВОЧЕК. СКОЛЬКИМИ СПОСОБАМИ ЭТО МОЖНО СДЕЛАТЬ?
1
2
4
3
840
111000000
1113840
400400

ЗАДАЧА № 6
Решение:
Нужно сделать два выбора: 4 мальчика из 18 (всего способов) и 3 девочки из 14 (всего способов); порядок выбора значения не имеет (все идущие на уборку равноправны). Каждый вариант выбора мальчиков может сочетаться с каждым выбором девочек, поэтому по правилу произведения общее число способов выбора равно:
Ответ: 1113840 способов

ЗАДАЧА № 7
ИЗ 25 УЧАСТНИКОВ СОБРАНИЯ НАДО ВЫБРАТЬ ПРЕДСЕДАТЕЛЯ И СЕКРЕТАРЯ. СКОЛЬКИМИ СПОСОБАМИ ЭТО МОЖНО СДЕЛАТЬ?
1
3
4
2
140
2
600
625

ЗАДАЧА № 7
Решение:
Из 25 элементов выбираем 2, причем порядок выбора имеет значение.
Количество способов выбора равно
Ответ: 600 способов

ЗАДАЧА № 8
СКОЛЬКИМИ СПОСОБАМИ 5 ВЫПУСКНИКОВ, СДАЮЩИХ ГИА, МОГУТ ЗАНЯТЬ МЕСТА В АУДИТОРИИ, В КОТОРОЙ СТОИТ 15 ОДНОМЕСТНЫХ СТОЛОВ?
1
2
4
3
36
3636
360360
360

ЗАДАЧА № 8
Решение:
Выбираем 5 столов для выпускников из 15 имеющихся: (порядок выбора учитывается (кто сидит около преподавателя, кто на последней парте, кто около окна и т.п.):
Ответ: 360 360 способов

ЗАДАЧА № 9
НА СОРЕВНОВАНИЯХ ПО ЛЕГКОЙ АТЛЕТИКЕ ПРИЕХАЛА КОМАНДА ИЗ 12 СПОРТСМЕНОК. СКОЛЬКИМИ СПОСОБАМИ ТРЕНЕР МОЖЕТ ОПРЕДЕЛИТЬ, КТО ИЗ НИХ ПОБЕЖИТ В ЭСТАФЕТЕ 4×100 М НА ПЕРВОМ, ВТОРОМ, ТРЕТЬЕМ И ЧЕТВЕРТОМ ЭТАПАХ?
3
2
1
4
144
11800
11880
48

ЗАДАЧА № 9
Решение:
Выбор из 12 по 4 с учетом порядка.
Ответ: 11 880

САМОСТОЯТЕЛЬНАЯ РАБОТА

САМОПРОВЕРКА

ОЦЕНКА СВОЕЙ РАБОТЫ
«5» - правильно выполнены все три задания.
«4» - правильно выполнены два задания.
«3» - правильно выполнено только одно задание.
«2» - все задания выполнены неверно или не выполнены.

ДОМАШНЕЕ ЗАДАНИЕ
Придумайте и решите
по одной задачи на каждую из тем
Перестановки
Размещения
сочетания