Слайд 2План урока
1. Неравенства вида аf(x) > аg(x).
2. Неравенства вида аf(x)>b, а>0.
3. Неравенства

вида аf(x) > bg(x).
4. Решение показательных неравенств методом замены переменной.
5. Решение неравенств, содержащих однородные функции относительно показательных функций.
6. Графическое решение показательных неравенств
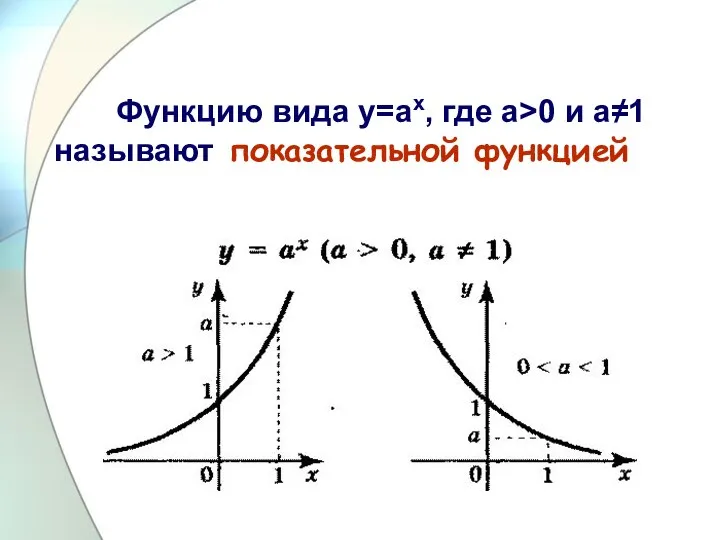
Слайд 3 Функцию вида у=ах, где а>0 и а≠1 называют
показательной функцией
Слайд 5Второе замечание
Обычно не рассматривают показательную функцию с основаниями:
а=1, т.к. , т.е. показательная

функция «вырождается» в постоянную функцию у=1- это неинтересно;
если а=0, то для любого положительного значения х, т.е. мы получаем функцию у=0, определённую при х>0, - это тоже неинтересно;
если а<0, то выражение а имеет смысл лишь при целых значениях х, а мы всё-таки предпочитаем рассматривать функции, определённые на сплошных промежутках
Слайд 6Основные свойства показательной функции у=аx

Слайд 7График показательной функции у=аx
а > 1
0 < а < 1
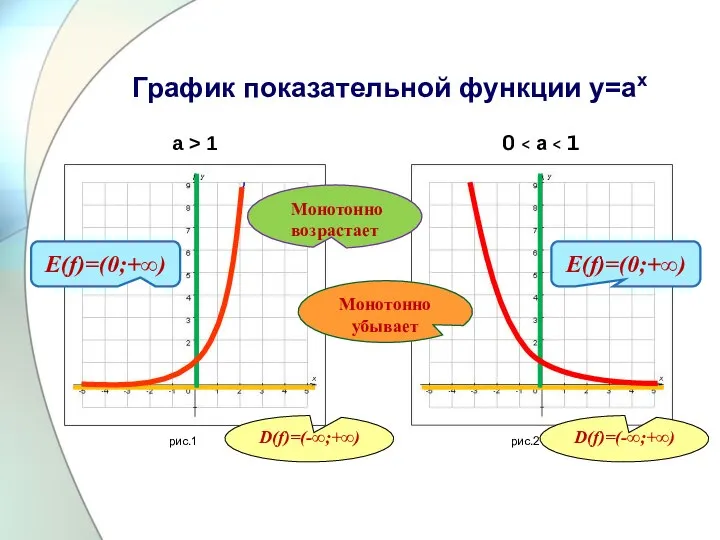
рис.1
рис.2
D(f)=(-∞;+∞)
D(f)=(-∞;+∞)
E(f)=(0;+∞)
E(f)=(0;+∞)
Монотонно возрастает
Монотонно убывает
Слайд 8 Неравенства, содержащие переменные в
показателе степени, называют показательными
1. Неравенства вида аf(x)

> аg(x)
Слайд 9 Задания ЕГЭ 2009 г.
А-6. Решите неравенство:
Правильный ответ:
Решение:

Слайд 10 Задания ЕГЭ 2009 г.
А-6. Решите неравенство:
Правильный ответ:
Решение:

Слайд 11 Задания ЕГЭ 2009 г.
А-6. Решите неравенство:
Правильный ответ:
Решение:

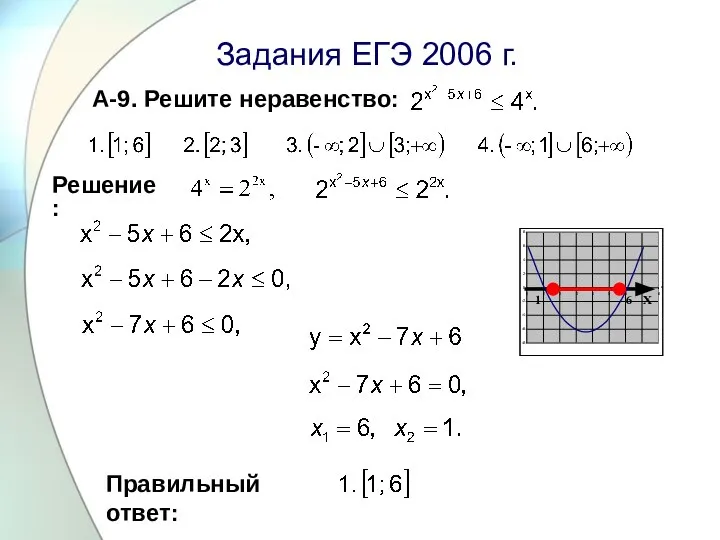
Слайд 12 Задания ЕГЭ 2006 г.
А-9. Решите неравенство:
Правильный ответ:
Решение:
Слайд 13 Пример
1. Найдите область определения функции:
Правильный ответ:
Решение:

Слайд 14 Пример
2. Найдите область определения функции:
Правильный ответ:
Решение:

Слайд 15 Пример
3. Укажите множество значений функции:
Правильный ответ:
Решение:

Слайд 162. Неравенства вида аf(x)>b, а>0.

Слайд 17 Пример 1
Решите неравенство:
Правильный ответ:
Решение:

Слайд 18 Пример 2
Решите неравенство:
Правильный ответ:
Решение:

Слайд 19 Пример 3
Решите неравенство:
Правильный ответ:
Решение:

Слайд 20Пример из заданий ЕГЭ 2006 г.
Решите неравенство:
Правильный ответ:
Решение:

Слайд 213.Неравенства вида аf(x) > bg(x)

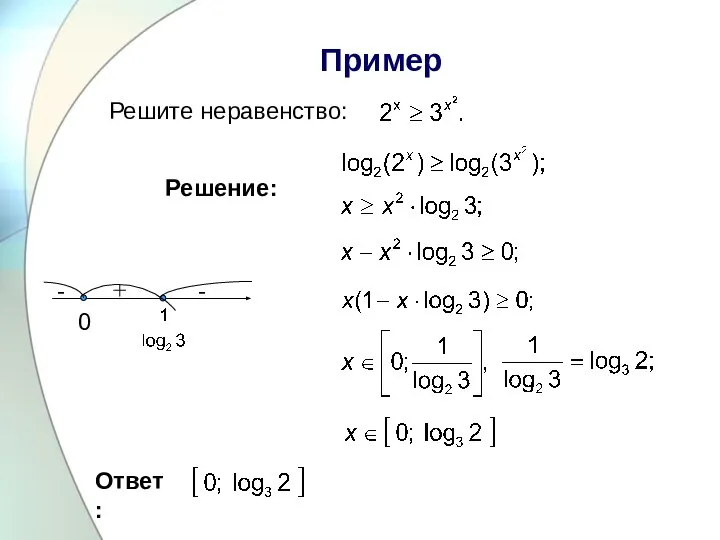
Слайд 22 Пример
Ответ :
0
- + -
Решите неравенство:
Решение:
Слайд 23Решите неравенство:
Ответ:
Решение:
Решение показательных неравенств
методом замены переменной

Слайд 24Решите неравенство:
Ответ:
Решение:
Решение неравенств, содержащих однородные функции относительно показательных функций

Слайд 25 Неравенства, в которых в одной части неравенства содержится показательная функция, а
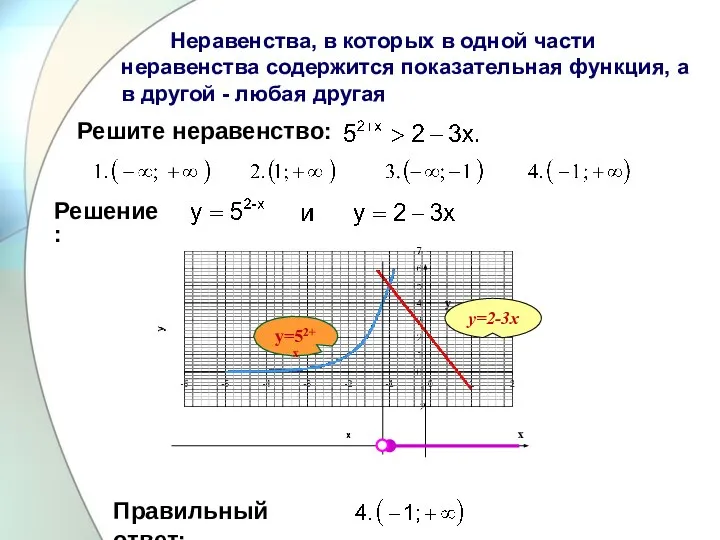
в другой - любая другая
у=2-3х
у=52+х
х
у
Решите неравенство:
Правильный ответ:
Решение:
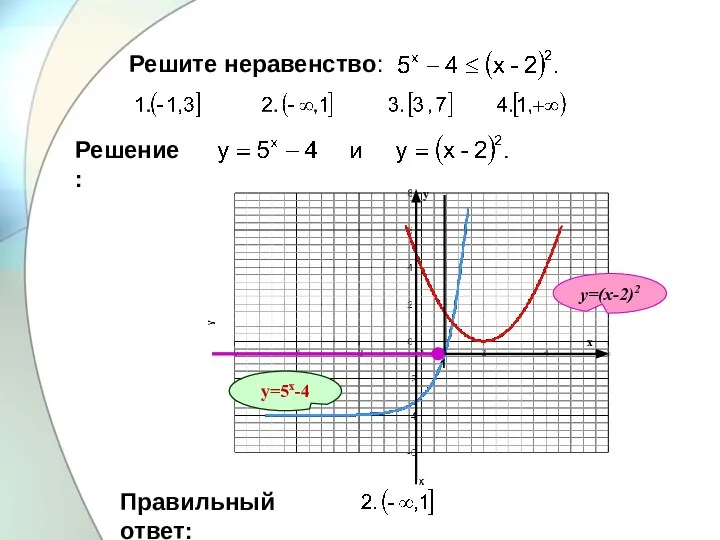
Слайд 26Решите неравенство:
х
у
1
у=(х-2)2
у=5х-4
Решение:
Правильный ответ:

























 Физико-математический турнир. Интегрированный урок
Физико-математический турнир. Интегрированный урок ЕГЭ по профильной математике. Прототипы №3
ЕГЭ по профильной математике. Прототипы №3 Transformace. Ekvivalence
Transformace. Ekvivalence Метод следов. Построение следа секущей плоскости
Метод следов. Построение следа секущей плоскости Симметрия в технике
Симметрия в технике Устный счет на уроках математики
Устный счет на уроках математики Полярные координаты
Полярные координаты парні і непарні функції-1
парні і непарні функції-1 Действия со смешанными числами
Действия со смешанными числами Математика. Занятие 32
Математика. Занятие 32 Понятие ”тетраэдр”
Понятие ”тетраэдр” Случаи вычитания 15 -
Случаи вычитания 15 - Числа вокруг нас
Числа вокруг нас Интегрированный урок алгебры и экономики. 7 класс
Интегрированный урок алгебры и экономики. 7 класс Сравнение групп предметов. Свойства предметов (1 класс)
Сравнение групп предметов. Свойства предметов (1 класс) Размерные цепи
Размерные цепи Презентация на тему ПРЯМОУГОЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕД
Презентация на тему ПРЯМОУГОЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕД  Таблица умножения девяти. Тренажёр-раскраска
Таблица умножения девяти. Тренажёр-раскраска Примеры
Примеры Дисперсия случайной величины и ее свойства
Дисперсия случайной величины и ее свойства Приемы устного счета
Приемы устного счета Прямоугольник. Квадрат
Прямоугольник. Квадрат Физический и геометрический смысл производной
Физический и геометрический смысл производной Тесты свойств графических элементов в пространстве
Тесты свойств графических элементов в пространстве Функция у=log ах, ее свойства и график
Функция у=log ах, ее свойства и график Симметрия в искусстве
Симметрия в искусстве Пирамиды. Решение задач. C 12
Пирамиды. Решение задач. C 12 Пересекающиеся прямые. Отрезок и его длина
Пересекающиеся прямые. Отрезок и его длина