Спин и расширенное супервремя. Суперсимметрия и суперпространство

Суперсимметрия и суперпространство
Группа Пуанкаре: P  T 4
so(3,1);
so(3,1)- группа Лоренца
Jˆ
Jˆ Jˆ Jˆ
 
        k
Pˆ , Pˆ   0, Pˆ , Jˆ
  g Pˆ  g Pˆ ,
 
       
 Jˆ
, Jˆ   g
g  g  g

  


Генераторы: Pˆ – трансляций, Jˆ – вращений.
Теорема «no-go» Коулмена-Мандулы:
«Не существует нетривиального объединения группы внутренних симметрий с группой Пуанкаре». Но!
Алгебра суперсимметрии SUSY:
   
ˆ ˆ ˆ ˆ
ˆ ˆ ˆ ˆ

 

  
P, Q  P, Q
 Q, Q  Q , Q
 0;
   
Qˆ, Qˆ   Pˆ;
Qˆ†
Qˆ Бозон  Фермион ; Фермион  Бозон .
Пространство Минковского
4  ct, x, y, z x ;   0,1, 2,3
Cуперпространство Минковского

4 4
 i
 j
  x , ,
; i, j  1, 2,3, 4;   1, 2.
SUSY SUGRA  Superstring M-theory

Суперматематика
Алгебра Грассмана n=1, i  1, 2,..., n:
i
 i , j   i j   j i  0
Пример: внешнее умножением 1-форм:
ei  e j  e j  ei ;
 ei , e j  0
1 2 k
 B i i ...i
Суперчисла: z   , z ,C  
1 2
1
k
1 2 k
i
i i
i i ...i
C   ...

z  zB  zS  zB  
 ;
zB - тело числа,
k 1 k !
zS - дух числа
Анализ над алгеброй Грассмана Gn
Грассмановы числа 1, 2 ,... n ; i ,  j  0
0
(1)
i
i1i2...in i1 i2 in
i1,i2 ,...,in
f ( n )
  ... .
f  f 
f   .... 
 i i 
Производная
Интеграл по Березину
ij
j
i
  ,

i i i
 d  1, d  0.
 
Алгебра БерезинаБn,m
(k)
n
p n
i1...ik i1...ik
f
k 1 i1...ik
f (x, ) 
(x)   G .
 
; x  m ,
Чётные элементы - бозонные степени свободы, Нечётные элементы- фермионные степени свободы.

Псевдоклассическая механика над Бn,m
F
F F
п L  d п L  0,   1,..., m. q  бозонные координаты
п L  d п L  0, i  1,..., n; qi  фермионные координаты
qi dt qi
q dt q
  0
Механика – это теория поля, на одномерном пространстве – прямой, параметризуемой собственным временем.
Плоское супервремя 11  (t, )
t - четное (бозонное) время
 - нечетное (грассманово) время
ds  dt  i d ,
S : t  t  t  i
       

(t, ) : 11   ,
(t, )  x(t)  i (t)
d
d
 0
 0
Qˆ  dS 
   i  ;
Hˆ  dT 
 i  .

t
t
Qˆ,Qˆ 2Qˆ 2  2Hˆ ;
Hˆ ,Qˆ   Qˆ 2Qˆ  QˆQˆ 2  0.
 
Ковариантная производная:
Dˆ    i  .

t
Квантовая механика
Псевдоклассическая механика

Псевдоклассическая модель электрона
Ди-Векиа, Равндел (1967)
X  (t, ) : 11  , X  (t, )  x (t)  i  (t)
2

S  dt d (1
DˆX   DˆDˆX  )
 
2

L  1 (x x  i  )
2
Уравнения Баргманна-Мишеля-Телегди в ЭМ-поле
q



 F
 0
x  qF x  S

 
 qF  S   qF S   .
S 
Уравнения Матиссона-Папапетру в ОТО


x    x x    R 
x S 
 
   
 0.
S  x S 
x S 
Некоторые результаты применения данной модели.
Мусин Ю.Р., Козориз В.И. Суперсимметричный электрон в кулоновском поле, ТМФ т 123, №1, 2000, с. 75-80 (Аналитические решения)
Мусин Ю.Р., Козориз В.И. Проблема рассеяния для классической частицы со спином в кулоновском поле, ТМФ, т 138 , №2, 2004, с 338-348 (Сечение рассеяния Мотта)
Мусин Ю.Р., Чередов В.В. Электрон со спином в поле шварцильдовской черной дыры, Тезисы докладов ГР-8 (Численное моделирование)

Композитные модели лептонов и кварков
 k l
2  
S  1 ds d Ekl g DX  DDX ,
Ekl g
DX  DDX   g DY  DDY
k l 
2 2
kl
E

1
a

( F ( N )  1))a 

 
( F ( N )  1))a2



 (F ( N )  1))a
a a2
( F ( N )  1))a2
( F ( N )  1)) a


0
Формула Барута
N 1
m( N )  m (1  aF ( N )) ;F (N )  k 4 ;  1/137
k 0
Массы лептонов и кварков (МэВ)
m0  me ;
mu  0, 685 Мэв ; md  6, 46 Мэв ; a  3 / 2
«Загадка радиуса протона» 4% или в 3,5 раза. (2010) 0,8802 ± 0,0080 фм  0,8775 ± 0,0051фм

Расширенное супервремя
c a
1 n  t, 1,..., n t   ;  k   ; k  1,..., n.
1-форма метрики
n
  dt  i k d k ;
  .
k 1
Преобразования сохраняющие метрику
k


   k


n
k k
k 1
 

k
k l
t  t

 t  t    t  t  i  

   cos   sin

  k    k   k   l   k sin   l cos

Алгебра суперсимметрии SUSY
Qˆk ,Qˆl  2kl Hˆ
Qˆk , ˆ kj   Qˆ j
 
ˆ ˆ
ˆ ˆ
ˆ ˆ
k kj
 


 
H , H  H ,Q
 H ,   0
     
Обобщенное действие:
n  1 - электрон, n  2- фотон m  0
1
ˆ
n n
D Х
k 1 k 1
 k 
S   dtd Х
2
k  
Уравнения движения:
k


 0; A  0.S  1 2


x  0; 
Первые интегралы
n
k k
L
  .
J   L
S  ;
 x  x  x x  ; S   i 
k 1

Структура супервремени
Плоское супервремя спинорных частиц S  1 2
Существуют только три поколения и только при n  1 (лептоны,кварки)
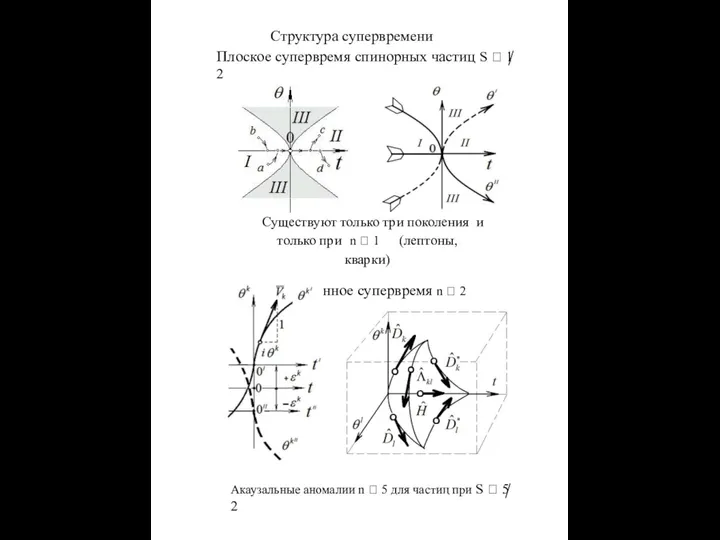
Расширенное супервремя n  2
Акаузальные аномалии n  5 для частиц при S  5 2