Решение задач на применение признаков равенства треугольников

Вдохновение нужно в геометрии
не меньше, чем в поэзии.
А. С. Пушкин.

ОТВЕТИМ НА ВОПРОСЫ ТЕСТА

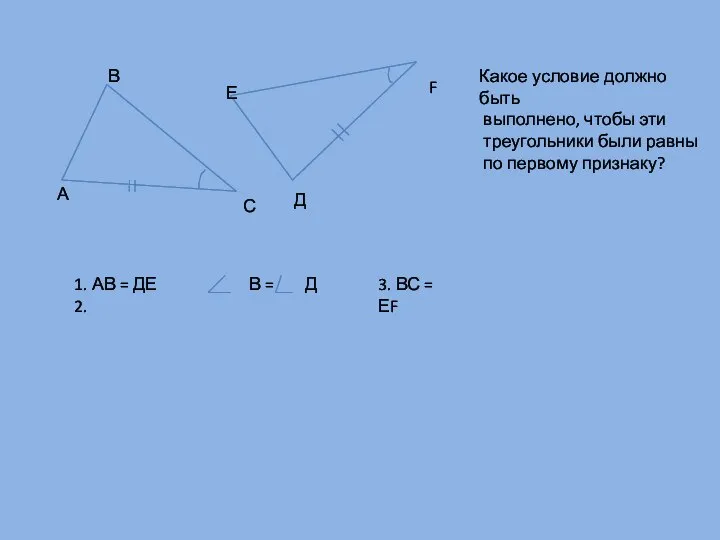
А
В
С
Д
F
Е
Какое условие должно быть
выполнено, чтобы эти
треугольники были равны по первому признаку?
1. АВ = ДЕ 2.
В =
Д
3. ВС = ЕF

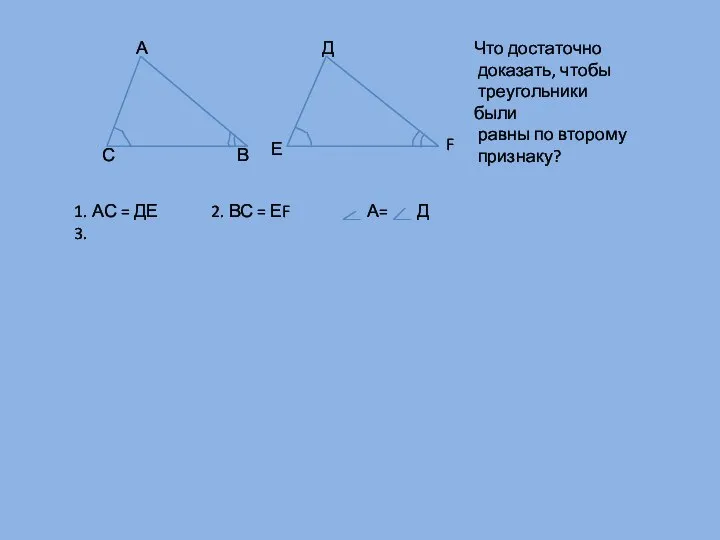
А
С
В
Е
F
Д
Что достаточно
доказать, чтобы
треугольники были
равны по второму
признаку?
1. АС = ДЕ 2. ВС = ЕF 3.
А=
Д

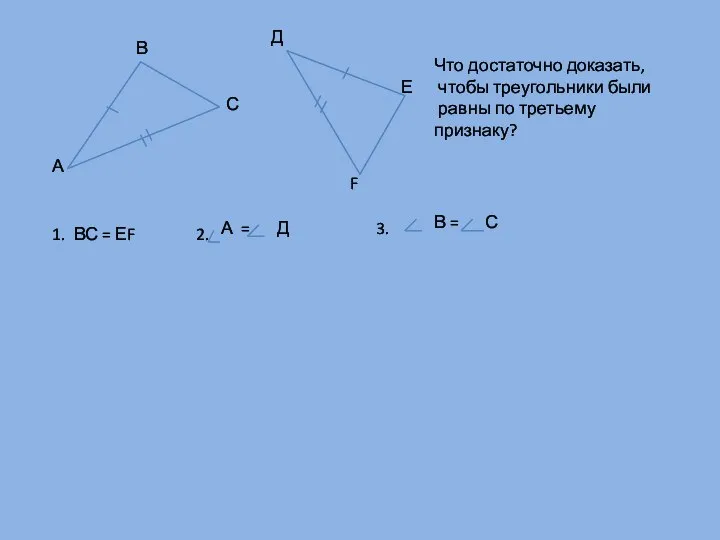
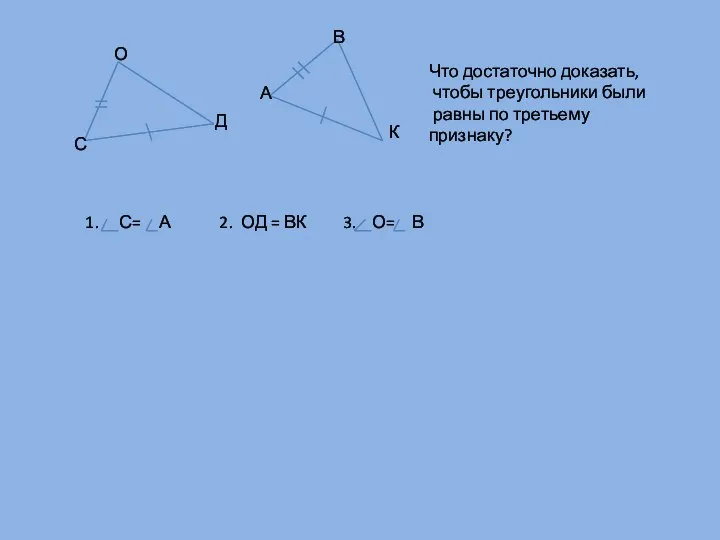
А
В
С
Д
Е
F
Что достаточно доказать,
чтобы треугольники были
равны по третьему признаку?
1. ВС = ЕF 2.
А = 3.
Д
В =
С

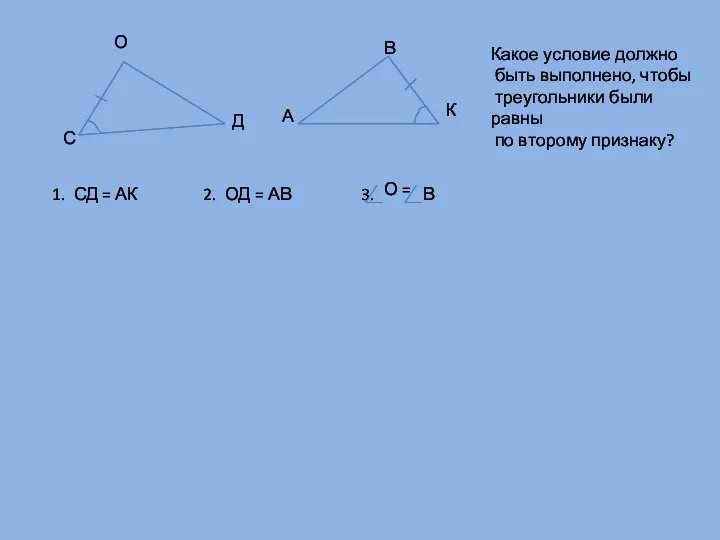
С
О
Д
А
К
В
Какое условие должно
быть выполнено, чтобы
треугольники были равны
по второму признаку?
1. СД = АК 2. ОД = АВ 3.
О =
В

С
О
Д
А
В
К
Что достаточно доказать,
чтобы треугольники были
равны по третьему признаку?
1.
С=
А 2. ОД = ВК 3.
О=
В

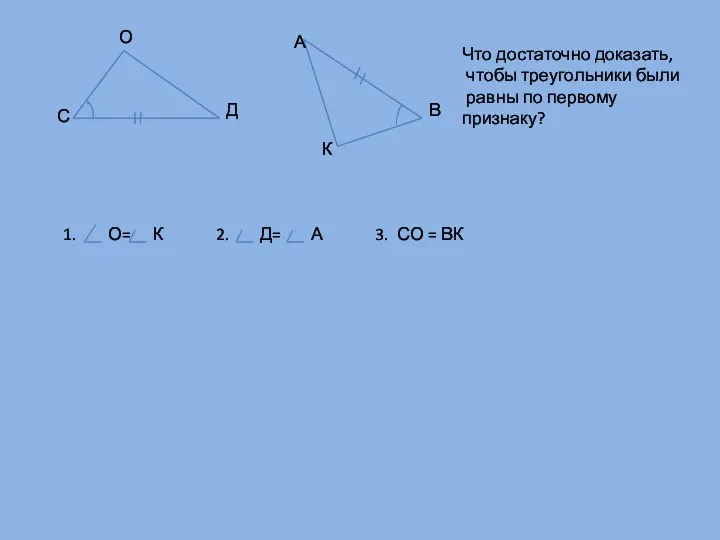
С
О
Д
А
В
К
Что достаточно доказать,
чтобы треугольники были
равны по первому признаку?
1.
О=
К 2.
Д=
А 3. СО = ВК

Решение задач по готовому рисунку

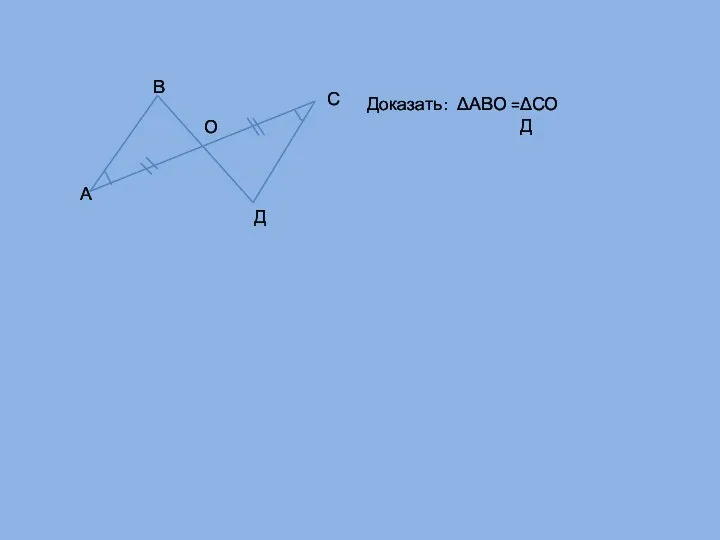
А
В
О
С
Д
Доказать:
ΔАВО =
ΔСОД

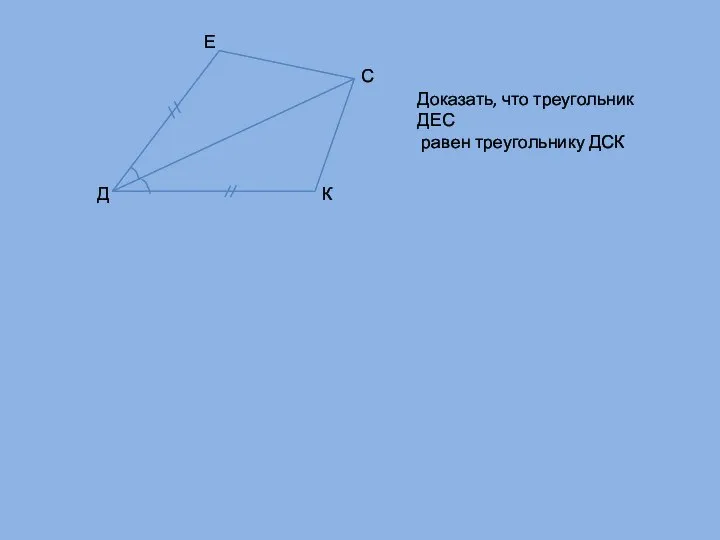
Д
Е
С
К
Доказать, что треугольник ДЕС
равен треугольнику ДСК

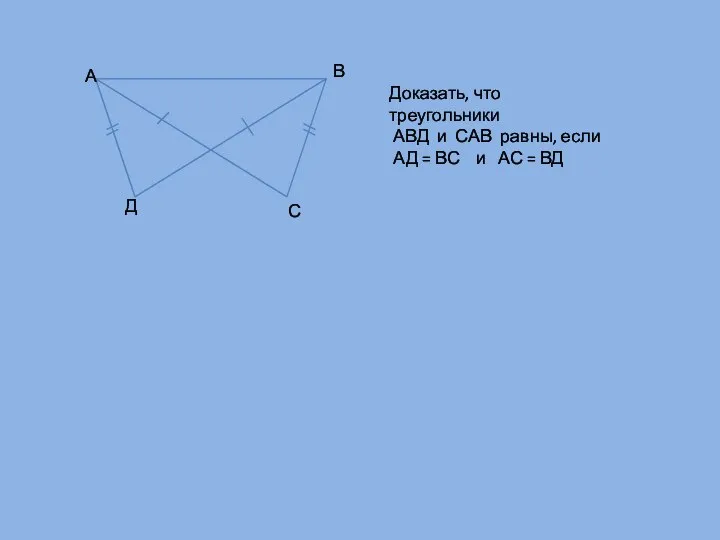
А
В
Д
С
Доказать, что треугольники
АВД и САВ равны, если
АД = ВС и АС = ВД

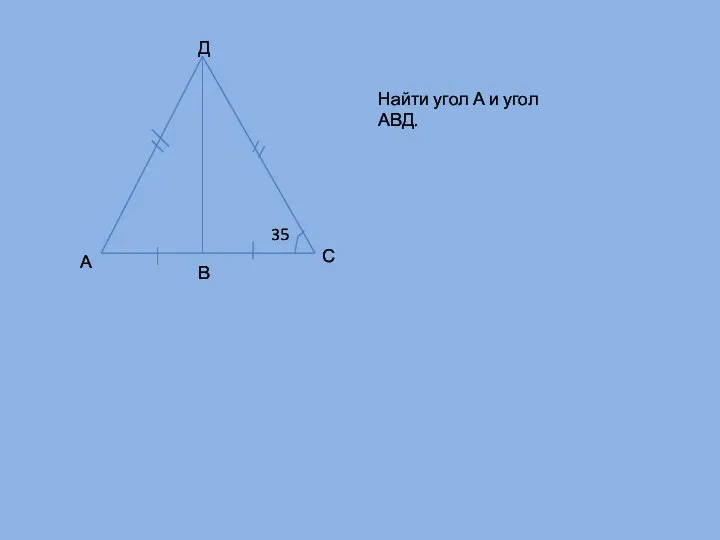
Д
А
В
С
35
Найти угол А и угол АВД.

РЕШАЕМ ЗАДАЧИ

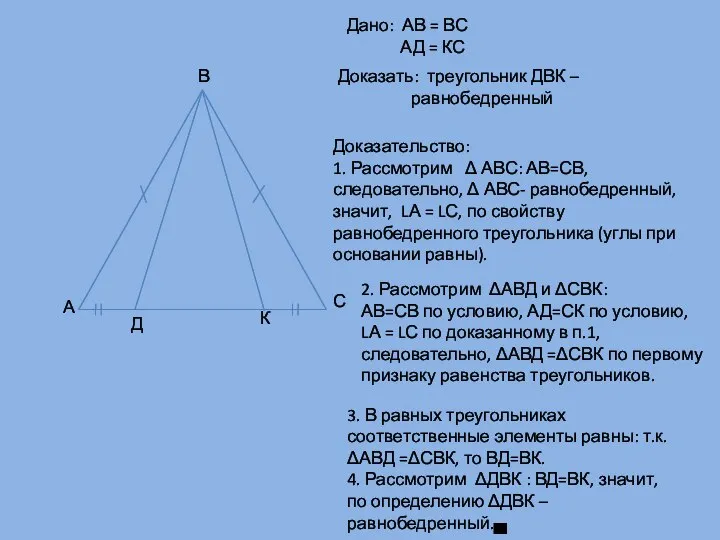
А
В
С
Д
К
3. В равных треугольниках соответственные элементы равны: т.к.
ΔАВД =ΔСВК, то ВД=ВК.
4. Рассмотрим ΔДВК : ВД=ВК, значит, по определению ΔДВК – равнобедренный.▄
Дано: АВ = ВС
АД = КС
Доказать: треугольник ДВК –
равнобедренный
Доказательство:
1. Рассмотрим Δ АВС: АВ=СВ, следовательно, Δ АВС- равнобедренный, значит, LА = LС, по свойству равнобедренного треугольника (углы при основании равны).
2. Рассмотрим ΔАВД и ΔСВК:
АВ=СВ по условию, АД=СК по условию,
LА = LС по доказанному в п.1, следовательно, ΔАВД =ΔСВК по первому признаку равенства треугольников.

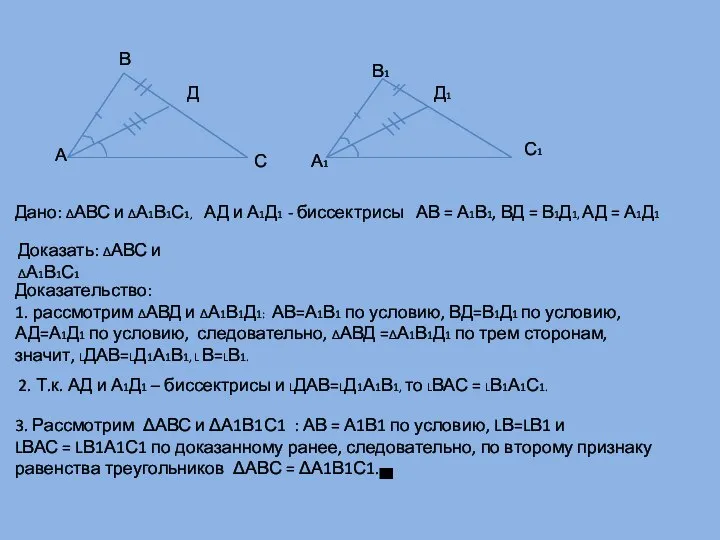
А
В
С
А1
В1
Д1
С1
Д
3. Рассмотрим ΔАВС и ΔА1В1С1 : АВ = А1В1 по условию, LВ=LВ1 и
LВАС = LВ1А1С1 по доказанному ранее, следовательно, по второму признаку равенства треугольников ΔАВС = ΔА1В1С1.▄
Дано: ΔАВС и ΔА1В1С1, АД и А1Д1 - биссектрисы АВ = А1В1, ВД = В1Д1, АД = А1Д1
Доказать: ΔАВС и ΔА1В1С1
Доказательство:
1. рассмотрим ΔАВД и ΔА1В1Д1: АВ=А1В1 по условию, ВД=В1Д1 по условию, АД=А1Д1 по условию, следовательно, ΔАВД =ΔА1В1Д1 по трем сторонам, значит, LДАВ=LД1А1В1, L В=LВ1.
2. Т.к. АД и А1Д1 – биссектрисы и LДАВ=LД1А1В1, то LВАС = LВ1А1С1.

«Если вы хотите научиться
плавать, то смело входите
в воду,
а если хотите научиться
решать задачи,
то решайте их».
Д. Пойа.