Слайд 2ЗАДАНИЕ 2 № 62
Для какого из приведённых значений числа X истинно высказывание:
НЕ(X > 5) И (X > 4)?
1) 4
2) 5
3)

6
4) 7
Слайд 3Пояснение.
Логическое «И» истинно только тогда, когда истинны оба высказывания.
Запишем выражение

в виде (X =< 5) И (X > 4)
и проверим все варианты ответа.
1) Ложно, поскольку ложно второе высказывание: 4 больше 4.
2) Истинно, поскольку истинны оба высказывания: 5 не больше 5 и 5 больше 4.
3) Ложно, поскольку ложно первое высказывание: 6 не больше 5.
4) Ложно, поскольку ложно первое высказывание: 7 не больше 5.
Правильный ответ указан под номером 2.
Слайд 4Задание 2 № 222
Для какого из приведённых чисел инстинно высказывание:
НЕ (число <10) ИЛИ НЕ (число чётное)?
1) 123
2) 56
3)

9
4) 8
Слайд 5Пояснение.
Логическое «ИЛИ» истинно тогда, когда истинно хотя бы одно высказывание.
Запишем выражение

в виде (число >= 10) ИЛИ (число нечётное) и проверим все варианты ответа.
1) Истинно, поскольку истинно первое высказывание: 123 не меньше 10.
2) Истинно, поскольку истинно первое высказывание: 56 не меньше 10.
3) Истинно, поскольку истинно второе высказывание: 9 — нечётное.
4) Ложно, поскольку ложны оба высказывания: 8 не меньше 10 и 8 чётное.
Правильный ответ указан под номером 4.
Слайд 6Задание 2 № 403
Для какого из приведённых имён истинно высказывание:
НЕ (Первая буква согласная) И НЕ (Последняя буква гласная)?
1)

Юлиан
2) Константин
3) Екатерина
4) Светлана
Слайд 7Пояснение.
Логическое «И» истинно только тогда, когда истинны оба высказывания.
Запишем выражение в

виде (Первая буква гласная) И (Последняя буква согласная)
и проверим все варианты ответа.
1) Истинно, поскольку истинны оба высказывания.
2) Ложно, поскольку ложно второе высказывание: к — гласная.
3) Ложно, поскольку ложно первое высказывание: а — согласная.
4) Ложно, поскольку ложны оба высказывания: с — согласная и а — гласная.
Правильный ответ указан под номером 1.
Слайд 8Задание 2 № 1136
Для какого из приведённых чисел истинно высказывание:
(Первая цифра чётная) И НЕ (Сумма

цифр чётная)?
1) 648
2) 452
3) 357
4) 123
Слайд 9Пояснение.
Логическое «И» истинно только тогда, когда истинны оба высказывания. Проверим все варианты

ответа.
1) Ложно, поскольку ложно второе высказывание.
2) Истинно, поскольку истинны оба высказывания.
3) Ложно, поскольку ложно первое высказывание.
4) Ложно, поскольку ложно первое высказывание.
Правильный ответ указан под номером 2.
Слайд 10Задание 2 № 302
Для какого из приведённых значений числа X истинно высказывание:
(X < 5) И НЕ (X < 4)?
1) 5
2)

2
3) 3
4) 4
Слайд 11Пояснение.
Логическое «И» истинно только тогда, когда истинны оба высказывания.
Запишем выражение в

виде (X < 5) И (X >= 4)
и проверим все варианты ответа.
1) Ложно, поскольку ложно первое высказывание: 5 меньше 5.
2) Ложно, поскольку ложно второе высказывание: 2 не меньше 4.
3) Ложно, поскольку ложно второе высказывание: 3 не меньше 4.
4) Истинно, поскольку истинны оба высказывания: 4 меньше 5 и 4 не меньше 4.
Правильный ответ указан под номером 4.
Слайд 12Задание 2 № 282
Для какого из приведённых значений числа X истинно высказывание:
НЕ (X < 3) И (X < 4)?
1) 5
2) 2
3)

3
4) 4
Слайд 13Пояснение.
Логическое «И» истинно только тогда, когда истинны оба высказывания.
Запишем выражение в

виде (X >= 3) И (X < 4) и проверим все варианты ответа.
1) Ложно, поскольку ложно второе высказывание: 5 меньше 4.
2) Ложно, поскольку ложно первое высказывание: 2 не меньше 3.
3) Истинно, поскольку истинны оба высказывания: 3 не меньше 3 и 3 меньше 4.
4) Ложно, поскольку ложно второе высказывание: 4 меньше 4.
Правильный ответ указан под номером 3.
Слайд 14Задание 2 № 383
Для какого из приведённых имён истинно высказывание:
НЕ (Первая буква согласная) И НЕ (Последняя буква гласная)?
1)

Ольга
2) Михаил
3) Валентина
4) Ян
Слайд 15Пояснение.
Логическое «И» истинно только тогда, когда истинны оба высказывания.
Запишем выражение

в виде
(Первая буква гласная) И (Последняя буква согласная)
и проверим все варианты ответа.
1) Ложно, поскольку ложно второе высказывание: а — согласная.
2) Ложно, поскольку ложно первое высказывание: м — гласная.
3) Ложно, поскольку ложно первое высказывание: в — гласная.
4) Истинно, поскольку истинны оба высказывания: я — гласная и н — согласная.
Правильный ответ указан под номером 4.
Слайд 16Задание 2 № 463
Для какого из приведённых имён ложно высказывание:
НЕ (Первая буква согласная) ИЛИ НЕ (Последняя буква гласная)?
1)

Пимен
2) Кристина
3) Ирина
4) Александр
Слайд 17Пояснение.
Логическое «ИЛИ» ложно только тогда, когда ложны оба высказывания. Запишем выражение в

виде
(Первая буква гласная) ИЛИ (Последняя буква согласная)
и проверим все варианты ответа.
1) Истинно, поскольку истинно второе высказывание: н — согласная.
2) Ложно, поскольку ложны оба высказывания: к — согласная и а — гласная.
3) Истинно, поскольку истинно первое высказывание: и — гласная.
4) Истинно, поскольку истинны оба высказывания: а — гласная и р — согласная.
Правильный ответ указан под номером 2.
Слайд 18Задание 2 № 663
Для какого из приведённых названий ложно высказывание:
НЕ (Количество букв чётное) ИЛИ (Первая буква согласная)?
1)

Омск
2) Иваново
3) Москва
4) Кировск
Слайд 19Пояснение.
Логическое «ИЛИ» ложно только тогда, когда ложны оба высказывания. Запишем выражение в

виде
(Количество букв нечётное) ИЛИ (Первая буква согласная)
и проверим все варианты ответа.
1) Ложно, поскольку ложны оба высказывания: в слове Омск четыре буквы, первая гласная.
2) Истинно, поскольку истинно первое высказывание: в слове Иваново семь букв, первая гласная.
3) Истинно, поскольку истинно второе высказывание: в слове Москва шесть букв, первая согласная.
4) Истинно, поскольку истинны оба высказывания: в слове Кировск семь букв, первая согласная.
Правильный ответ указан под номером 1.
Слайд 20Задание 2 № 798
Для какого из приведённых чисел истинно высказывание:
НЕ (число > 10) И (число нечётное)?
1) 22
2)

13
3) 9
4) 6
Слайд 21Пояснение.
Логическое «И» истинно только тогда, когда истинны оба высказывания.
Запишем выражение в

виде (число < 10) И (число нечётное) и проверим все варианты ответа.
1) Ложно, поскольку 22 — чётное число.
2) Ложно, поскольку ложно первое высказывание: 13 < 10.
3) Истинно, поскольку истинны оба высказывания.
4) Ложно, поскольку 6 — чётное число.
Правильный ответ указан под номером 3.
Слайд 22Задание 2 № 222
Для какого из приведённых чисел истинно высказывание:
НЕ (число <10) ИЛИ НЕ (число чётное)?
1) 123
2) 56
3)

9
4) 8
Слайд 23Пояснение.
Логическое «ИЛИ» истинно тогда, когда истинно хотя бы одно высказывание.
Запишем выражение

в виде (число >= 10) ИЛИ (число нечётное)
и проверим все варианты ответа.
1) Истинно, поскольку истинно первое высказывание: 123 не меньше 10.
2) Истинно, поскольку истинно первое высказывание: 56 не меньше 10.
3) Истинно, поскольку истинно второе высказывание: 9 — нечётное.
4) Ложно, поскольку ложны оба высказывания: 8 не меньше 10 и 8 — чётное.
Правильный ответ указан под номером 4.
Слайд 24Задание 2 № 603
Для какого из данных слов истинно высказывание:
НЕ (есть шипящие) И НЕ (оканчивается на гласную)?
Шипящие звуки —

это [ж], [ш], [ч'], [щ'].
1) любовь
2) отвращение
3) забота
4) отчуждённость
Слайд 25Пояснение.
Логическое «И» истинно только тогда, когда истинны оба высказывания.
Запишем выражение в

виде (нет шипящих) И (оканчивается на согласную)
и проверим все варианты ответа.
1) Истинно, поскольку истинны оба высказывания: слово любовь оканчивается на согласную и в нём нет шипящих.
2) Ложно, поскольку ложны оба высказывания: в слове отвращение есть шипящие и оно оканчивается на гласную.
3) Ложно, поскольку ложно второе высказывание: слово забота оканчивается на гласную.
4) Ложно, поскольку ложно первое высказывание: в слове отчуждённость есть шипящие.
Правильный ответ указан под номером 1.
Слайд 26Задание 2 № 182
Для какого из приведённых чисел истинно высказывание:
НЕ (число <50) И (число чётное)?
1) 24
2) 45
3)

74
4) 99
Слайд 27Пояснение.
Логическое «И» истинно только тогда, когда истинны оба высказывания.
Запишем выражение в

виде (число >= 50) И (число чётное)
и проверим все варианты ответа.
1) Ложно, поскольку ложно первое высказывание: 24 больше или равно 50.
2) Ложно, поскольку ложно первое высказывание: 45 меньше или равно 50.
3) Истинно, поскольку истинны оба высказывания: 74 — чётное И 74 больше или равно 50.
4) Ложно, поскольку ложно второе высказывание: 99 — нечётное.
Правильный ответ указан под номером 3.
Слайд 28Задание 2 № 443
Для какого из приведённых имён ложно высказывание:
НЕ (Первая буква гласная) ИЛИ НЕ (Последняя буква согласная)?
1)

Эдуард
2) Ангелина
3) Карина
4) Никон
Слайд 29Пояснение.
Логическое «ИЛИ» ложно только тогда, когда ложны оба высказывания.
Запишем выражение в

виде (Первая буква согласная) ИЛИ (Последняя буква гласная)
и проверим все варианты ответа.
1) Ложно, поскольку ложны оба высказывания: э — гласная и д — согласная.
2) Истинно, поскольку истинно второе высказывание: а — гласная.
3) Истинно, поскольку истинны оба высказывания: к — согласная и а — гласная.
4) Истинно, поскольку истинно первое высказывание: в — согласная.
Правильный ответ указан под номером 1.
Слайд 30
Задание 2 № 423
Для какого из приведённых имён ложно высказывание:
НЕ (Первая буква гласная) ИЛИ НЕ (Последняя буква согласная)?
1)

Арина
2) Владимир
3) Раиса
4) Ярослав





























 Построение сечений многогранников. Построение сечений параллелепипеда
Построение сечений многогранников. Построение сечений параллелепипеда Задачи на построение
Задачи на построение Квадратные уравнения
Квадратные уравнения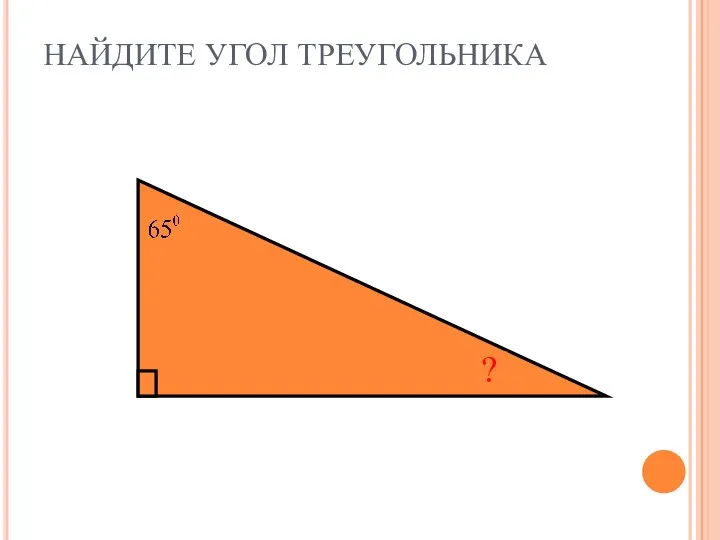 Нахождение угла треугольника
Нахождение угла треугольника Исторические задачи комбинаторики и теории вероятностей. Самостоятельная внеаудиторная работа 1
Исторические задачи комбинаторики и теории вероятностей. Самостоятельная внеаудиторная работа 1 Производная и исследование функции
Производная и исследование функции Решение заданий ЕГЭ уровня С2 (1 часть)
Решение заданий ЕГЭ уровня С2 (1 часть) Перестановка слагаемых
Перестановка слагаемых Отношения и пропорция
Отношения и пропорция Сложение и вычитание дробей
Сложение и вычитание дробей Логарифмические уравнения
Логарифмические уравнения Тупой угол равен прямому
Тупой угол равен прямому Вынесение общего множителя за скобки
Вынесение общего множителя за скобки Логарифмические уравнения
Логарифмические уравнения Презентация по математике "Приемы вычислений для случаев вида 60-24" -
Презентация по математике "Приемы вычислений для случаев вида 60-24" -  Свойство параллелограмма
Свойство параллелограмма Введение понятия целого и дробного выражения
Введение понятия целого и дробного выражения Плоскость. Лекция 8
Плоскость. Лекция 8 Шарады, метаграммы, логогрифы
Шарады, метаграммы, логогрифы Косинус острого угла прямоугольного треугольника. 8 класс
Косинус острого угла прямоугольного треугольника. 8 класс Задачи на построение
Задачи на построение uravnenie_urok_2
uravnenie_urok_2 Решение систем неравенств (8 класс)
Решение систем неравенств (8 класс) Ментальная арифметика в г. Камень-на-Оби
Ментальная арифметика в г. Камень-на-Оби Математическая игра Отгадайка
Математическая игра Отгадайка Предел последовательности. Урок 1
Предел последовательности. Урок 1 Эквивалентные бесконечно малые функции
Эквивалентные бесконечно малые функции Длина окружности и площадь круга. 6 класс
Длина окружности и площадь круга. 6 класс