Содержание
- 2. 2 см3 4 см3 медь серебро 59 г Плотность меди
- 3. Решение: Пусть плотность меди х г/см3 , плотность серебра у г/см3. По условию задачи разность у
- 4. у – х = 2 2х + 4у = 59
- 5. у – х = 2 2х + 4у = 59 у – х = 2, у
- 6. у – х = 2 2х + 4у = 59 у – х = 2, у
- 7. у – х = 2 2х + 4у = 59 у – х = 2, у
- 9. Пусть х км/ч – скорость дачника пешком, у км/ч – скорость дачника на велосипеде. По условию
- 10. у = 2,4х 2х + 3у = 46
- 11. у = 2,4х 2х + 3у = 46 у = 2,4х
- 12. у = 2,4х 2х + 3у = 46 у = 2,4х 2х + 3 · 2,4х
- 13. у = 2,4х 2х + 3у = 46 у = 2,4х 2х + 3 · 2,4х
- 15. Пусть х гектолитров поступает за одну минуту через первую трубу, у гектолитров через вторую трубу. По
- 16. 3у - 4х = 1 5х + у = 32
- 17. 3у - 4х = 1 5х + у = 32 5х + у = 32, у
- 18. 3у - 4х = 1 5х + у = 32 5х + у = 32, у
- 19. 3у - 4х = 1 5х + у = 32 5х + у = 32, у
- 21. Пусть х км/ч – собственная скорость теплохода, у км/ч – скорость течения, (х + у)км/ч -
- 22. х - у = 40 4(х + у) = 5(х – у)
- 23. х - у = 40 4(х + у) = 5(х – у) х - у =
- 24. х - у = 40 4(х + у) = 5(х – у) х - у =
- 25. х - у = 40 4(х + у) = 5(х – у) х - у =
- 26. х - у = 40 4(х + у) = 5(х – у) х - у =
- 27. х - у = 40 4(х + у) = 5(х – у) х - у =
- 28. Пусть х км/ч – скорость катера по течению, у км/ч – скорость катера против течения. По
- 29. 3х + 4у = 120 3х – 2у = 30
- 30. 3х + 4у = 120 3х – 2у = 30 1) _ 3х + 4у =
- 31. 3х + 4у = 120 3х – 2у = 30 1) _ 3х + 4у =
- 33. Пусть х –пятиместных лодок, у - трехместных лодок. По условию задачи сумма х и у равна
- 34. х + у = 10 |· 5 5х + 3у = 44
- 35. х + у = 10 |· 5 5х + 3у = 44 1) _ 5х +
- 37. Скачать презентацию


































 Что такое математика?
Что такое математика? Работа над ошибками СОР. Подготовка к СОЧ
Работа над ошибками СОР. Подготовка к СОЧ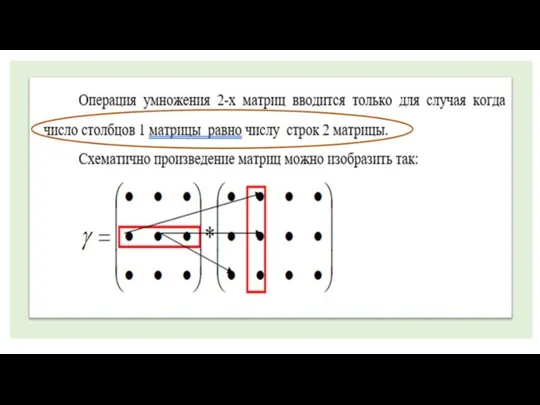 Операция умнодения 2 матриц
Операция умнодения 2 матриц Цифровые средства измерения
Цифровые средства измерения Дифференциал функции. (Семинар 16)
Дифференциал функции. (Семинар 16) Готовимся к ОГЭ по математике
Готовимся к ОГЭ по математике Движение. Тест № 6. 9 класс
Движение. Тест № 6. 9 класс Второй признак равенства треугольников
Второй признак равенства треугольников Тела вращения. Цилиндр. Площадь поверхности цилиндра
Тела вращения. Цилиндр. Площадь поверхности цилиндра Презентация на тему Окружность и круг (5 класс)
Презентация на тему Окружность и круг (5 класс)  Образование дробей. 5 класс
Образование дробей. 5 класс Иррациональные уравнения (часть 1)
Иррациональные уравнения (часть 1) Готовимся к ОГЭ по математике
Готовимся к ОГЭ по математике Замена двузначного числа суммой разрядных слагаемых
Замена двузначного числа суммой разрядных слагаемых Теорема Пифагора
Теорема Пифагора Поверхности и тела. Проецирование геометрических фигур
Поверхности и тела. Проецирование геометрических фигур Метод корреляционных плеяд
Метод корреляционных плеяд Определение свойств функции по графику
Определение свойств функции по графику 20f
20f Математическая конференция 6а класса
Математическая конференция 6а класса Решение задач
Решение задач Решение тригонометрических уравнений Простейшие тригонометрические уравнения
Решение тригонометрических уравнений Простейшие тригонометрические уравнения Устный счёт
Устный счёт Многогранники и их основные свойства
Многогранники и их основные свойства Правила комбинаторики. Практическое занятие
Правила комбинаторики. Практическое занятие Схемотехника
Схемотехника Составление фигур из спичек
Составление фигур из спичек Метод Гаусса
Метод Гаусса