Сечения многогранников

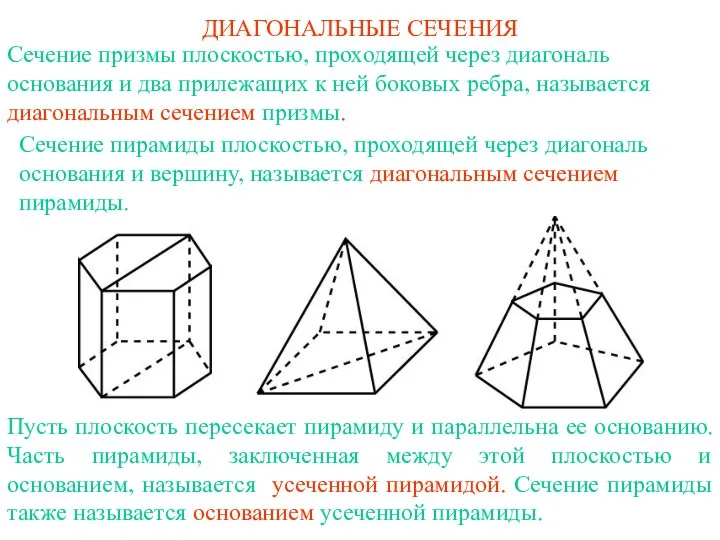
Сечение призмы плоскостью, проходящей через диагональ основания и два прилежащих к ней боковых ребра, называется диагональным сечением призмы.
Сечение пирамиды плоскостью, проходящей через диагональ основания и вершину, называется диагональным сечением пирамиды.
ДИАГОНАЛЬНЫЕ СЕЧЕНИЯ
Пусть плоскость пересекает пирамиду и параллельна ее основанию. Часть пирамиды, заключенная между этой плоскостью и основанием, называется усеченной пирамидой. Сечение пирамиды также называется основанием усеченной пирамиды.

Какой фигурой является сечение многогранника плоскостью?
Упражнение 1
Ответ: Многоугольником.

Сколько диагональных сечений имеет n-угольная: а) призма; б) пирамида?
Упражнение 2

Может ли в сечении куба плоскостью получиться:
а) треугольник;
б) правильный треугольник;
в) равнобедренный треугольник;
г) прямоугольный треугольник;
д) тупоугольный треугольник?
Упражнение 3
Ответ: а) Да;
б) да;
в) да;
г) нет;
д) нет.

Может ли в сечении куба плоскостью получиться:
а) квадрат;
б) прямоугольник;
в) параллелограмм;
г) ромб;
д) трапеция;
е) прямоугольная трапеция?
Упражнение 4
Ответ: а) Да;
б) да;
в) да;
г) да;
д) да;
е) нет.

Может ли в сечении куба плоскостью получиться:
а) пятиугольник;
б) правильный пятиугольник?
Упражнение 5
Ответ: а) Да;
б) нет.

Может ли в сечении куба плоскостью получиться:
а) шестиугольник;
б) правильный шестиугольник;
в) многоугольник с числом сторон больше шести?
Упражнение 6
Ответ: а) Да;
б) да;
в) нет.

Какие многоугольники можно получить в сечении четырехугольной пирамиды плоскостью?
Упражнение 7
Ответ: Треугольник, четырехугольник, пятиугольник.

Может ли в сечении правильного тетраэдра плоскостью получиться квадрат?
Упражнение 8
Ответ: Да.

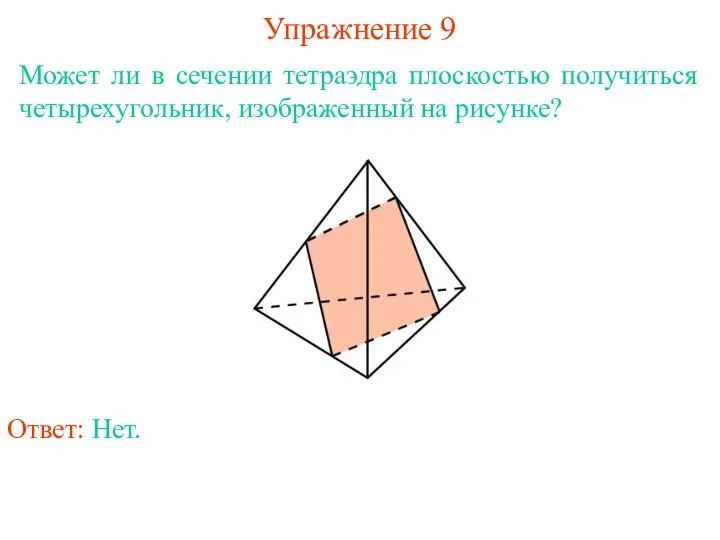
Может ли в сечении тетраэдра плоскостью получиться четырехугольник, изображенный на рисунке?
Упражнение 9
Ответ: Нет.

Может ли в сечении октаэдра плоскостью получиться:
а) треугольник;
б) четырехугольник;
в) пятиугольник;
г) шестиугольник;
д) семиугольник;
е) восьмиугольник?
Упражнение 10
Ответ: а) Нет;
б) да;
в) нет;
г) да;
д) нет;
е) нет.

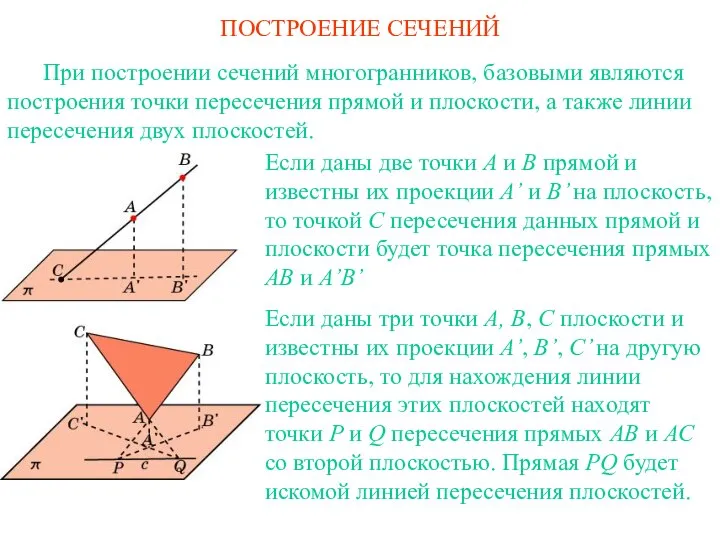
При построении сечений многогранников, базовыми являются построения точки пересечения прямой и плоскости, а также линии пересечения двух плоскостей.
Если даны две точки A и B прямой и известны их проекции A’ и B’ на плоскость, то точкой С пересечения данных прямой и плоскости будет точка пересечения прямых AB и A’B’
Если даны три точки A, B, C плоскости и известны их проекции A’, B’, C’ на другую плоскость, то для нахождения линии пересечения этих плоскостей находят точки P и Q пересечения прямых AB и AC со второй плоскостью. Прямая PQ будет искомой линией пересечения плоскостей.
ПОСТРОЕНИЕ СЕЧЕНИЙ

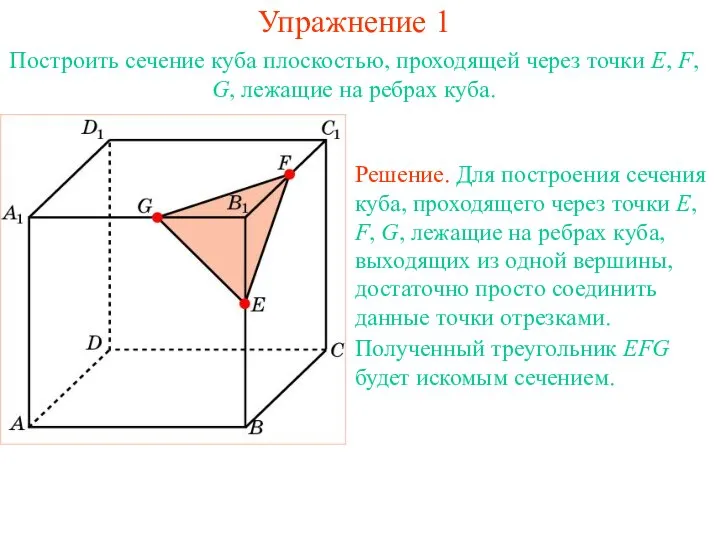
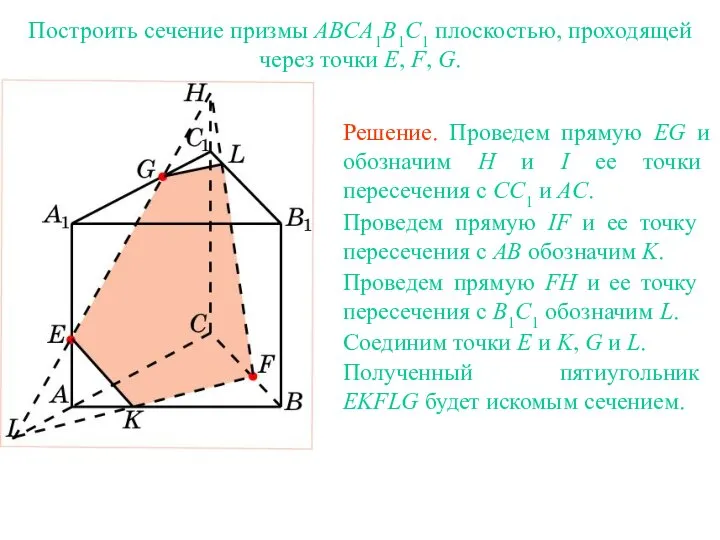
Решение. Для построения сечения куба, проходящего через точки E, F, G, лежащие на ребрах куба, выходящих из одной вершины,
Построить сечение куба плоскостью, проходящей через точки E, F, G, лежащие на ребрах куба.
Упражнение 1

Решение. Для построения сечения куба, проходящего через точки E, F, G,
проведем прямую EF и обозначим P её точку пересечения с AD.
Обозначим Q точку пересечения прямых PG и AB.
Соединим точки E и Q, F и G.
Построить сечение куба плоскостью, проходящей через точки E, F, G , лежащие на ребрах куба.
Полученная трапеция EFGQ будет искомым сечением.
Упражнение 2

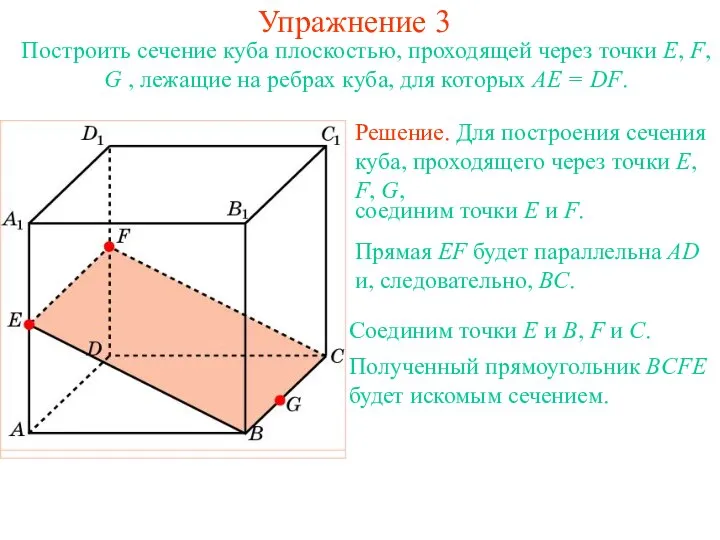
Решение. Для построения сечения куба, проходящего через точки E, F, G,
Упражнение 3

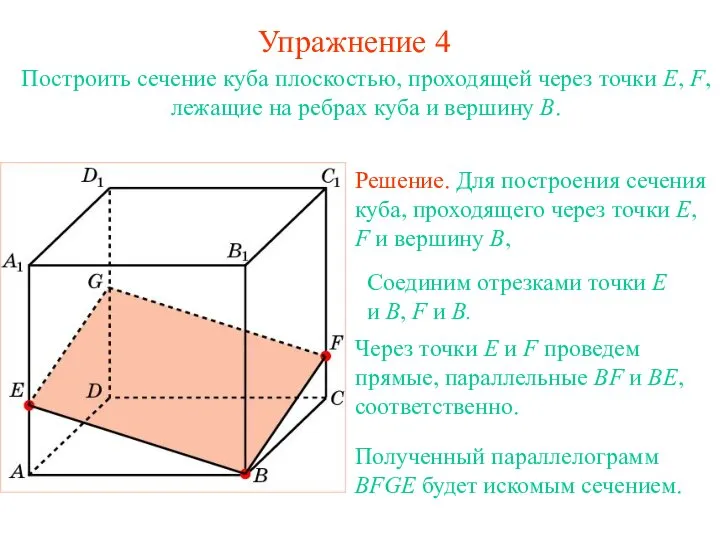
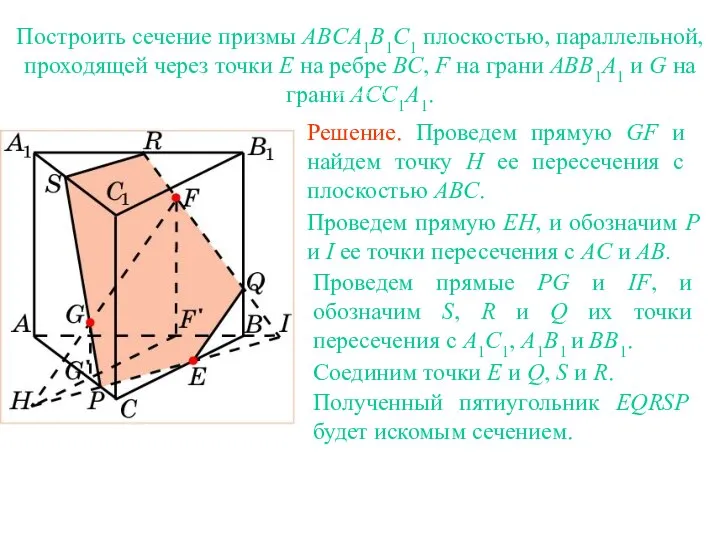
Решение. Для построения сечения куба, проходящего через точки E, F и вершину B,
Упражнение 4

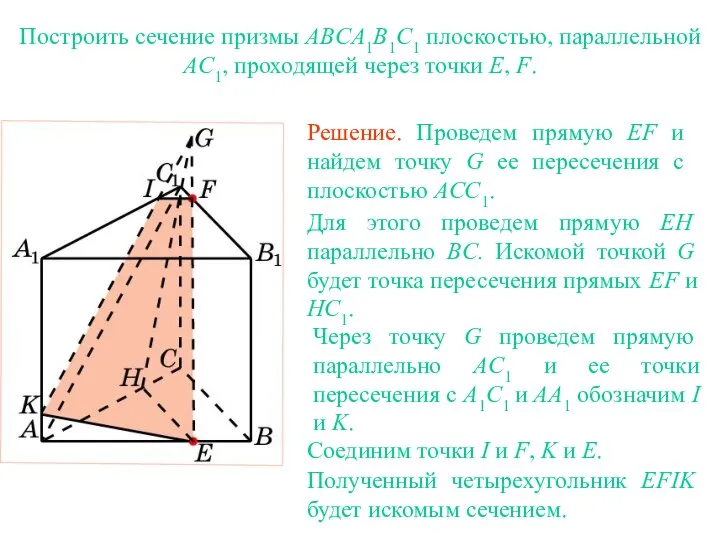
Решение. Для построения сечения куба, проходящего через точки E, F, G,
проведем прямую EF и обозначим P её точку пересечения с AD.
Обозначим Q, R точки пересечения прямой PG с AB и DC.
Соединим точки E и Q, G и S.
Построить сечение куба плоскостью, проходящей через точки E, F, G , лежащие на ребрах куба.
Полученный пятиугольник EFSGQ будет искомым сечением.
Обозначим S точку пересечения FR c СС1.
Упражнение 5

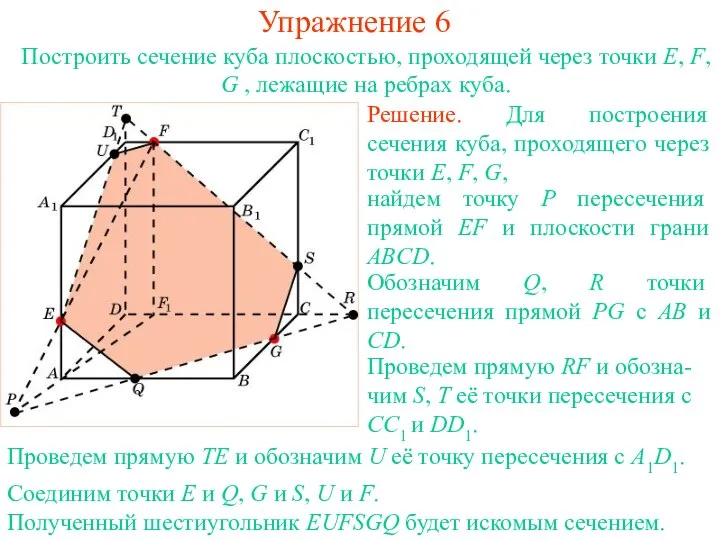
Решение. Для построения сечения куба, проходящего через точки E, F, G,
найдем точку P пересечения прямой EF и плоскости грани ABCD.
Проведем прямую RF и обозна-чим S, T её точки пересечения с CC1 и DD1.
Обозначим Q, R точки пересечения прямой PG с AB и CD.
Построить сечение куба плоскостью, проходящей через точки E, F, G , лежащие на ребрах куба.
Соединим точки E и Q, G и S, U и F.
Проведем прямую TE и обозначим U её точку пересечения с A1D1.
Полученный шестиугольник EUFSGQ будет искомым сечением.
Упражнение 6

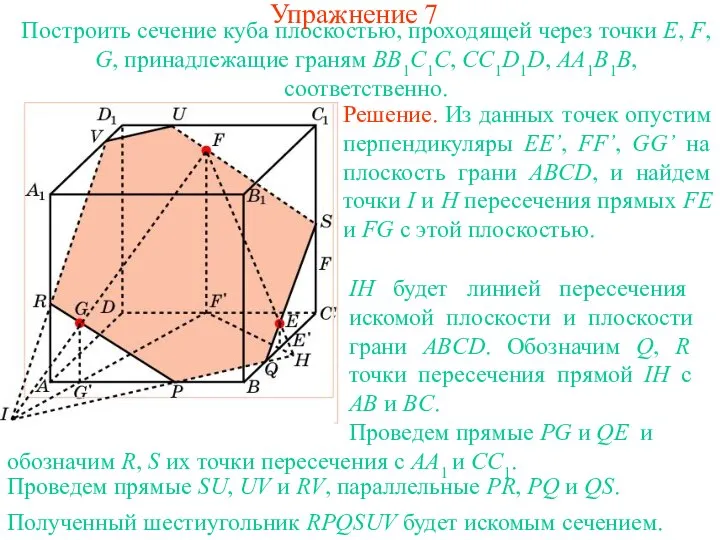
Упражнение 7

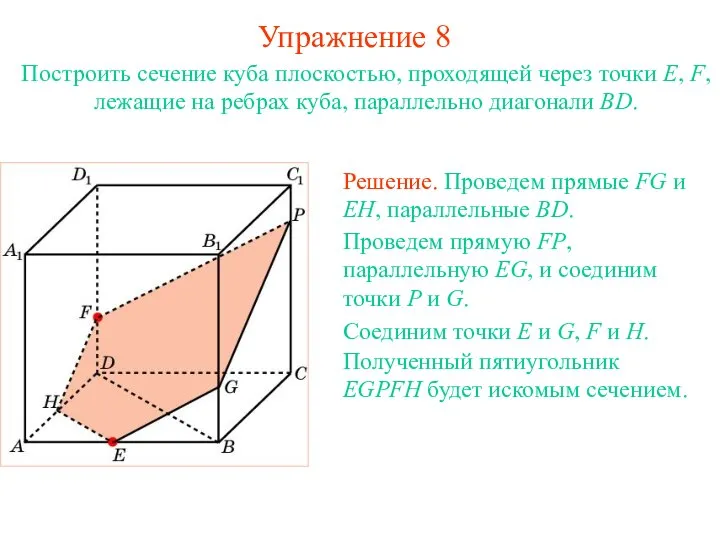
Упражнение 8

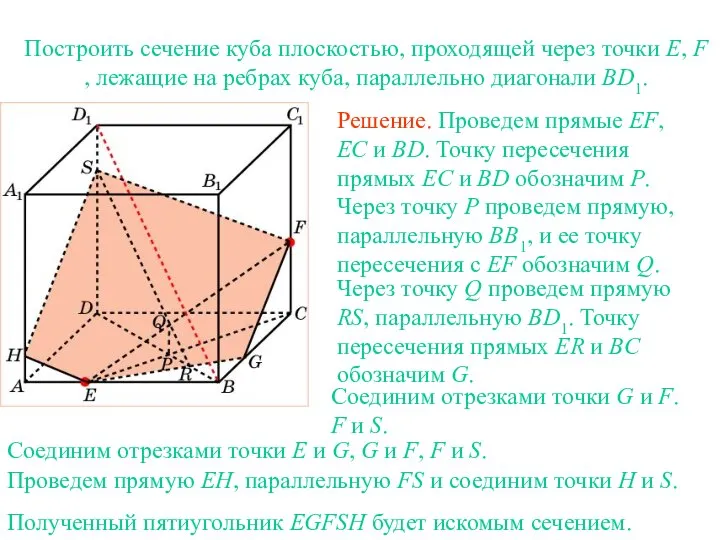
Упражнение 9

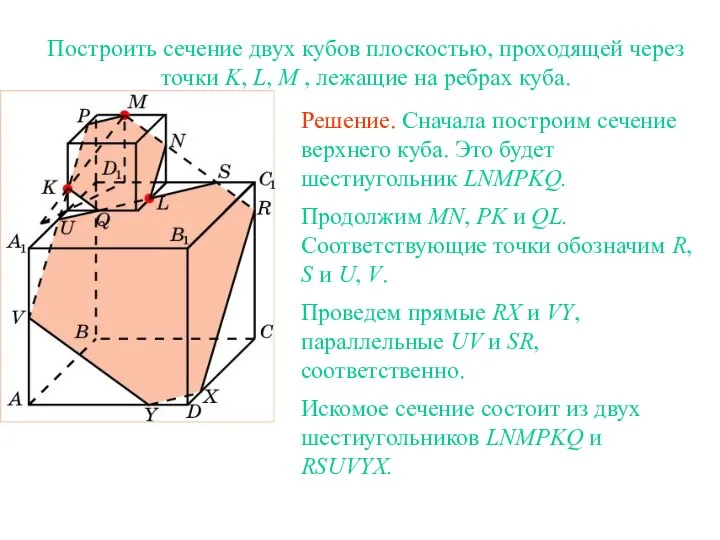
Построить сечение двух кубов плоскостью, проходящей через точки K, L, M , лежащие на ребрах куба.
Упражнение 10

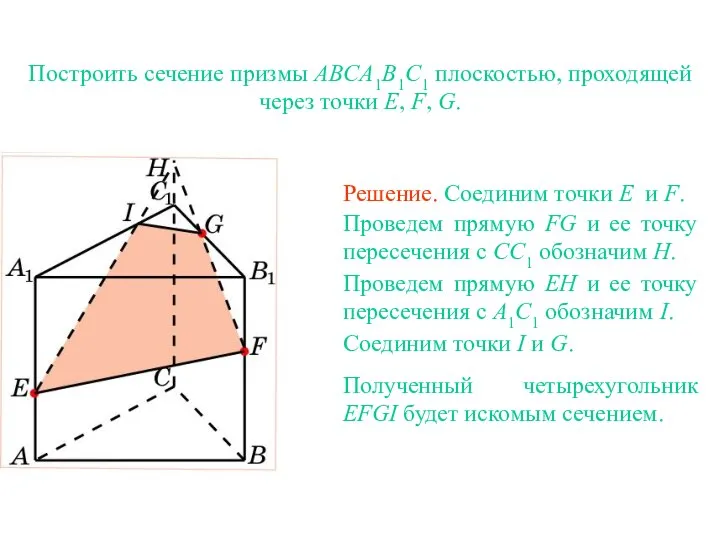
Упражнение 11

Упражнение 12

Упражнение 13

Упражнение 14

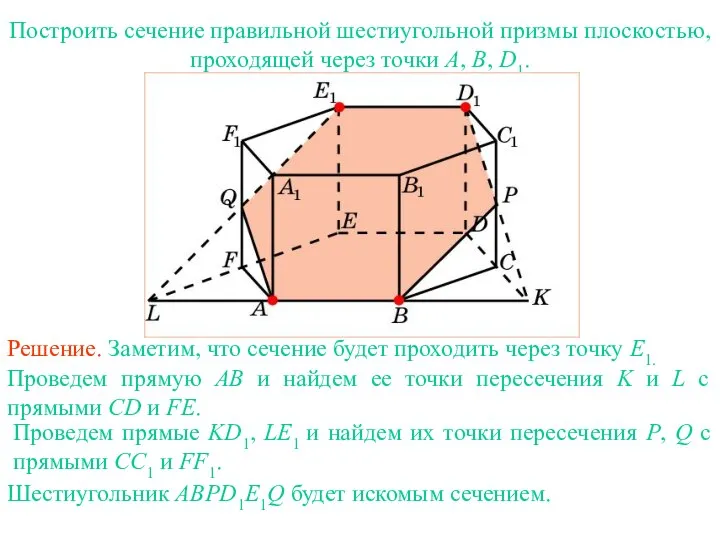
Построить сечение правильной шестиугольной призмы плоскостью, проходящей через точки A, B, D1.
Упражнение 15

Упражнение 16

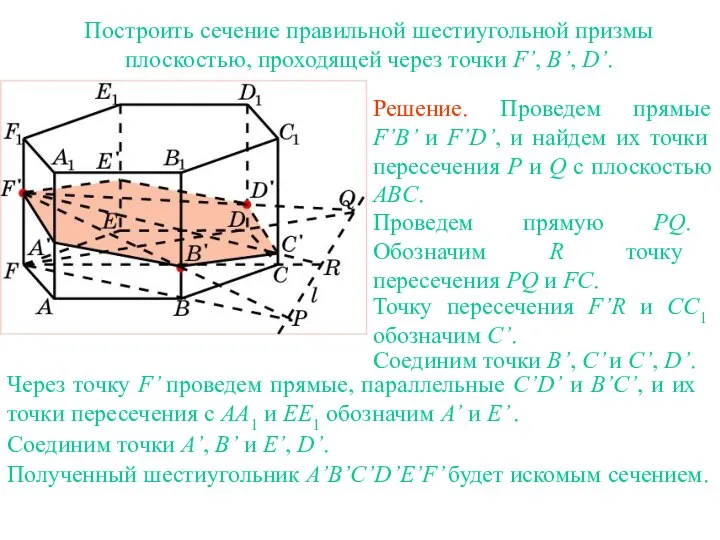
Построить сечение правильной шестиугольной призмы плоскостью, проходящей через точки F’, B’, D’.
Упражнение 17

Упражнение 18

Упражнение 19

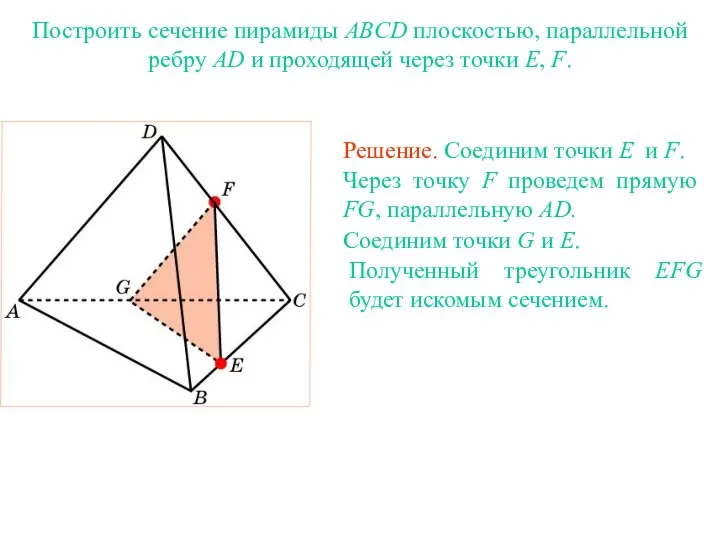
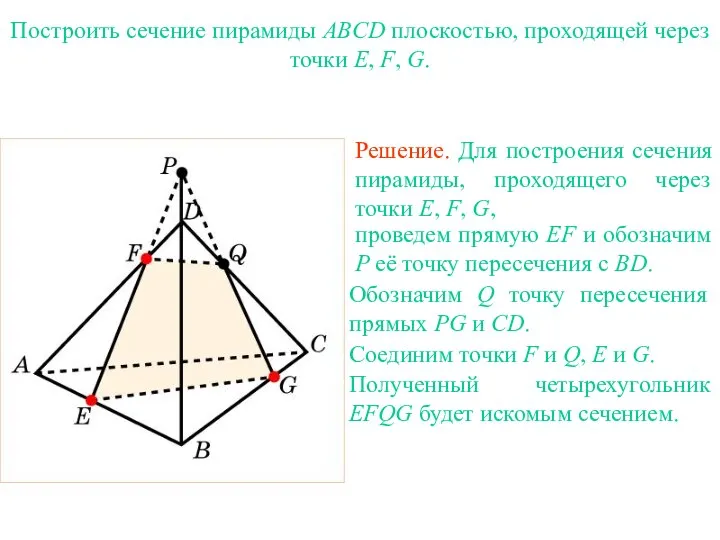
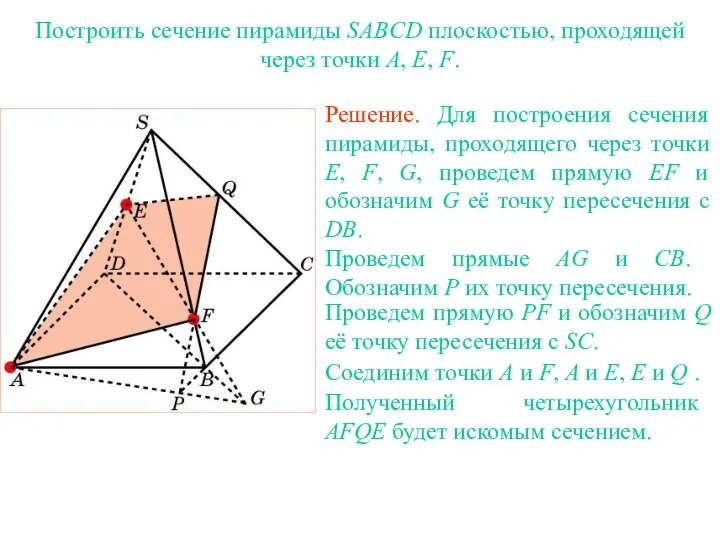
Решение. Для построения сечения пирамиды, проходящего через точки E, F, G,
проведем прямую EF и обозначим P её точку пересечения с BD.
Обозначим Q точку пересечения прямых PG и CD.
Соединим точки F и Q, E и G.
Построить сечение пирамиды ABCD плоскостью, проходящей через точки E, F, G.
Полученный четырехугольник EFQG будет искомым сечением.
Упражнение 20

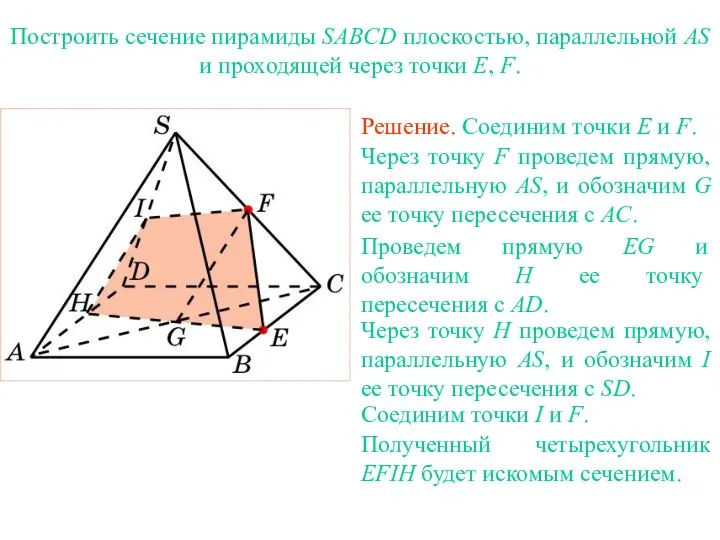
Упражнение 21

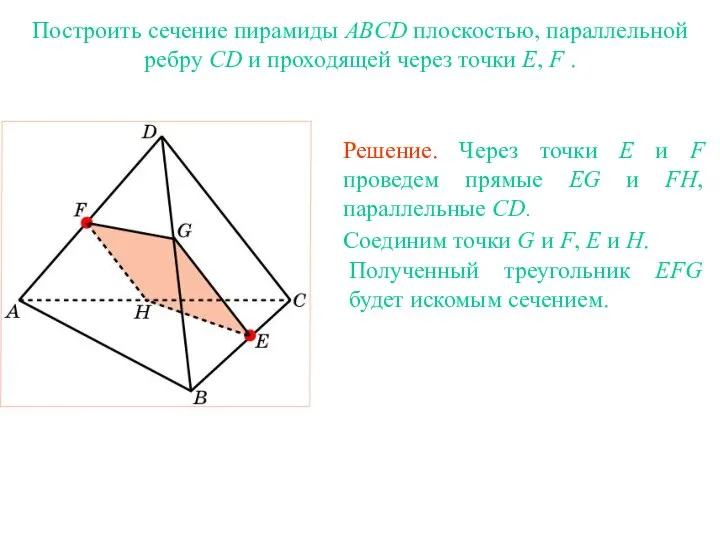
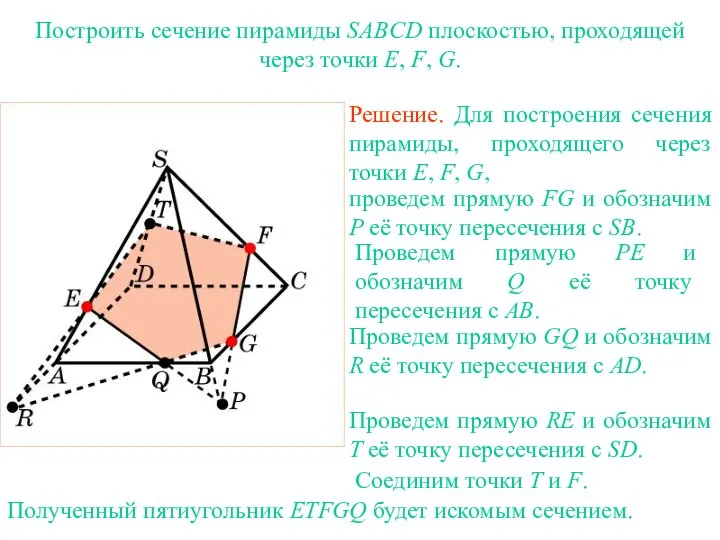
Решение. Для построения сечения пирамиды, проходящего через точки E, F, G,
проведем прямую FG и обозначим P её точку пересечения с SB.
Проведем прямую PE и обозначим Q её точку пересечения с AB.
Построить сечение пирамиды SABCD плоскостью, проходящей через точки E, F, G.
Полученный пятиугольник ETFGQ будет искомым сечением.
Соединим точки T и F.
Проведем прямую GQ и обозначим R её точку пересечения с AD.
Проведем прямую RE и обозначим T её точку пересечения с SD.
Упражнение 22

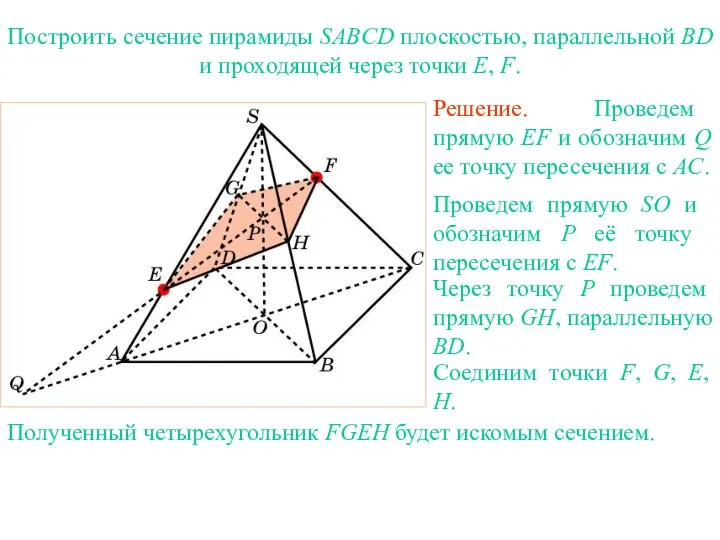
Упражнение 23

Упражнение 24