- Главная
- Математика
- Секреты квадратных уравнений

Содержание
- 2. Уже во втором тысячелетии до нашей эры вавилоняне знали, как решать квадратные уравнения. Решение их в
- 3. Задачи, решаемые с помощью квадратных уравнений, встречаются в трактате по астрономии «Ариабхаттиам», написанным индийским астрономом и
- 4. Использование прямой и обратной теоремы Виета Прямая теорема Виета и обратная ей теорема позволяют решать приведённые
- 6. Скачать презентацию
Слайд 2Уже во втором тысячелетии до нашей эры вавилоняне знали, как решать квадратные
Уже во втором тысячелетии до нашей эры вавилоняне знали, как решать квадратные

Слайд 3Задачи, решаемые с помощью квадратных уравнений, встречаются в трактате по астрономии «Ариабхаттиам»,
Задачи, решаемые с помощью квадратных уравнений, встречаются в трактате по астрономии «Ариабхаттиам»,

:
:
:
Слайд 4Использование прямой и обратной теоремы Виета
Прямая теорема Виета и обратная ей теорема
Использование прямой и обратной теоремы Виета
Прямая теорема Виета и обратная ей теорема

Согласно обратной теореме, всякая пара чисел (число) , будучи решением нижеприведённой системы уравнений, являются корнями уравнения
Подобрать устно числа, удовлетворяющие этим уравнениям, поможет прямая теорема. С её помощью можно определить знаки корней, не зная сами корни. Для этого следует руководствоваться правилом:
1)если свободный член отрицателен, то корни имеют различный знак, и наибольший по модулю из корней — знак, противоположный знаку второго коэффициента уравнения;
2)если свободный член положителен, то оба корня обладают одинаковым знаком, и это — знак, противоположный знаку второго коэффициента.
 Формулы сокращённого умножения
Формулы сокращённого умножения Созвездия. Сималтиниус Раунд Тэйбл
Созвездия. Сималтиниус Раунд Тэйбл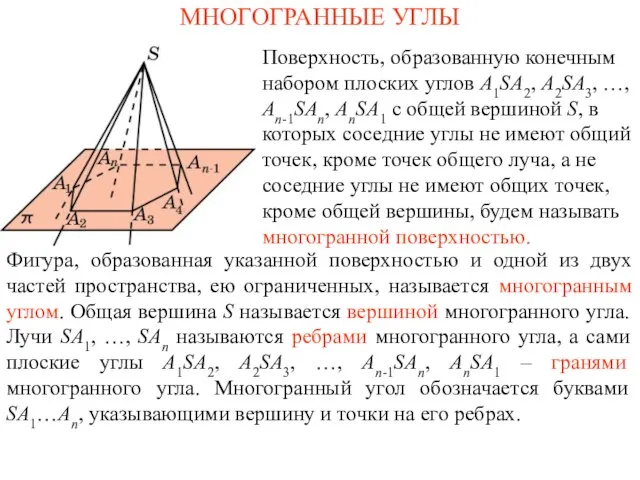 Презентация на тему Многогранные углы
Презентация на тему Многогранные углы  Тест по теме Векторы в пространстве. 11 класс
Тест по теме Векторы в пространстве. 11 класс Золотое сечение
Золотое сечение Кубические см
Кубические см Презентация на тему Сложение и вычитание натуральных чисел (5 класс)
Презентация на тему Сложение и вычитание натуральных чисел (5 класс)  Презентация на тему Подготовка к контрольной работе по алгебре
Презентация на тему Подготовка к контрольной работе по алгебре  Векторы. 9 класс
Векторы. 9 класс Определение общего числа единиц (десятков, сотен) в числе. 3 класс
Определение общего числа единиц (десятков, сотен) в числе. 3 класс Математическая викторина
Математическая викторина Один. Много
Один. Много Основные тригонометрические тождества. Преобразование тригонометрических выражений
Основные тригонометрические тождества. Преобразование тригонометрических выражений Математика. Управление социальными системами. Математический анализ. Дифференцирование функции одной переменной
Математика. Управление социальными системами. Математический анализ. Дифференцирование функции одной переменной Второй и третий признаки подобия треугольников
Второй и третий признаки подобия треугольников Презентация по математике "Портреты учёных математиков" -
Презентация по математике "Портреты учёных математиков" -  Тренинговая работа №3
Тренинговая работа №3 Устный счёт от 1 до 20
Устный счёт от 1 до 20 Мысли о ЕГЭ
Мысли о ЕГЭ Числовой коэффициент
Числовой коэффициент Несущая способность сечений при изгибе
Несущая способность сечений при изгибе Všetko o kocke
Všetko o kocke Закон пропорциональности
Закон пропорциональности Сумма углов треугольника. Решение задач
Сумма углов треугольника. Решение задач Числа 1 - 4. (1 класс)
Числа 1 - 4. (1 класс)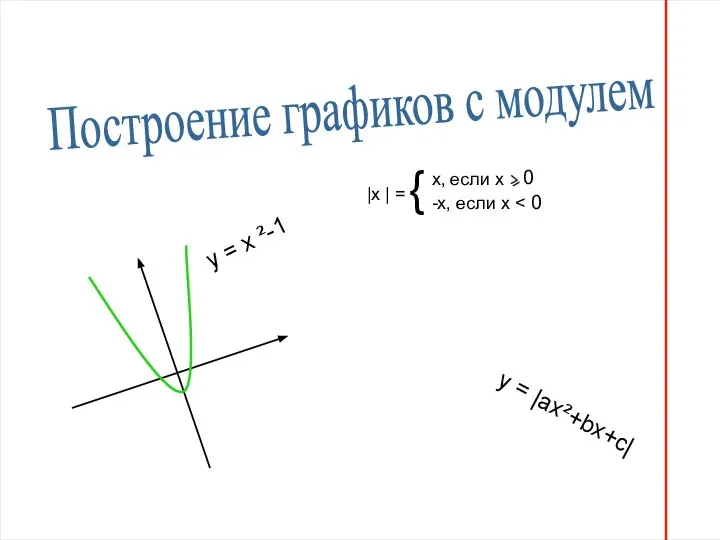 Построение графиков с модулем
Построение графиков с модулем Геометрические построения. 7 класс
Геометрические построения. 7 класс Сложение натуральных чисел и его свойства
Сложение натуральных чисел и его свойства