Содержание
- 2. Цель урока: ввести понятие сферы, шара и их элементов, вывести уравнение сферы в заданной прямоугольной системе
- 3. Задание № 1 (Конспектировать) Шар и сфера Шар — геометрическое тело, ограниченное поверхностью, все точки которой
- 4. Примеры тел, имеющих форму шара или сферы: Купол здания может иметь форму части сферы, отсеченной плоскостью.
- 5. Связанные определения Если секущая плоскость проходит через центр шара, то сечение шара называется большим кругом. Другие
- 6. Концы любого диаметра называются диаметрально противоположными точками шара. Плоскость, проходящая через центр шара, называется диаметральной плоскостью.
- 7. Свойства Всякое сечение шара плоскостью есть круг. Центр этого круга есть основание перпендикуляра, опущенного из центра
- 8. Основные формулы Площадь сферы радиуса R вычисляется по формуле
- 9. №2 задание Дайте полный ответ на вопросы
- 10. задание № 3 1.Радиус сферы увеличили в 3 раза. Во сколько раз увеличится площадь сферы? 2.Шар,
- 11. №4 задание ответьте на вопросы
- 14. Скачать презентацию











 Математический язык
Математический язык Сложение отрицательных чисел
Сложение отрицательных чисел В страну математики. Задания
В страну математики. Задания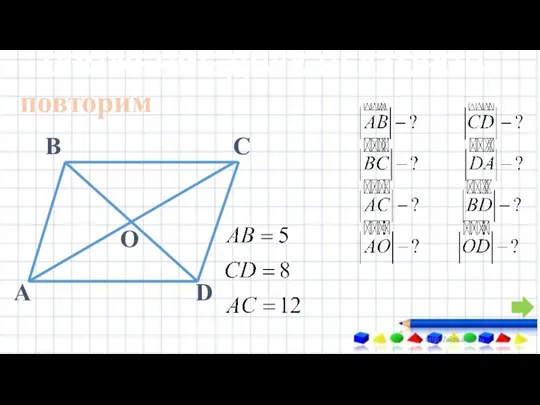 Сумма двух векторов. Закон сложения векторов. Правило параллелограмма
Сумма двух векторов. Закон сложения векторов. Правило параллелограмма Решение задач. Подготовка к контрольной работе
Решение задач. Подготовка к контрольной работе Треугольники вокруг нас
Треугольники вокруг нас Методика преподования геометрии
Методика преподования геометрии Математическая логика. Логические выражения
Математическая логика. Логические выражения Классная работа по математике
Классная работа по математике Статистика. Статистические дисциплины
Статистика. Статистические дисциплины Презентация на тему Системы линейных уравнений с двумя переменными
Презентация на тему Системы линейных уравнений с двумя переменными  Определители второго и третьего порядков
Определители второго и третьего порядков Тайны математики
Тайны математики График степенной функции
График степенной функции Урок 9-10 Відстань між двома точками на площині
Урок 9-10 Відстань між двома точками на площині Вероятность события есть количественная мера возможности наступления этого события
Вероятность события есть количественная мера возможности наступления этого события Степень многочлена
Степень многочлена Дифференциальные уравнения с разделяющимися переменными
Дифференциальные уравнения с разделяющимися переменными Производная сложной функции
Производная сложной функции Параллельный перенос и его свойства
Параллельный перенос и его свойства Площадь круга и его частей
Площадь круга и его частей Комбинаторика. Перебор вариантов. Решение задач
Комбинаторика. Перебор вариантов. Решение задач Дифференциальные уравнения первого порядка. Дифференциальные уравнения с разделяющимися переменными
Дифференциальные уравнения первого порядка. Дифференциальные уравнения с разделяющимися переменными Связь между параллельностью и перпендикулярностью прямых и плоскостей (Задание)
Связь между параллельностью и перпендикулярностью прямых и плоскостей (Задание) Функция y=k/x и её график
Функция y=k/x и её график Десятки, единицы, цифры
Десятки, единицы, цифры Синус, косинус и тангенс острого угла прямоугольного треугольника
Синус, косинус и тангенс острого угла прямоугольного треугольника Дифференциальные уравнения
Дифференциальные уравнения