Симметрия 11кл

Понятие движения
Движение – это отображение пространства на себя, сохраняющее расстояния между точками

Виды движения
Центральная симметрия
Осевая симметрия
Зеркальная симметрия
Параллельный перенос

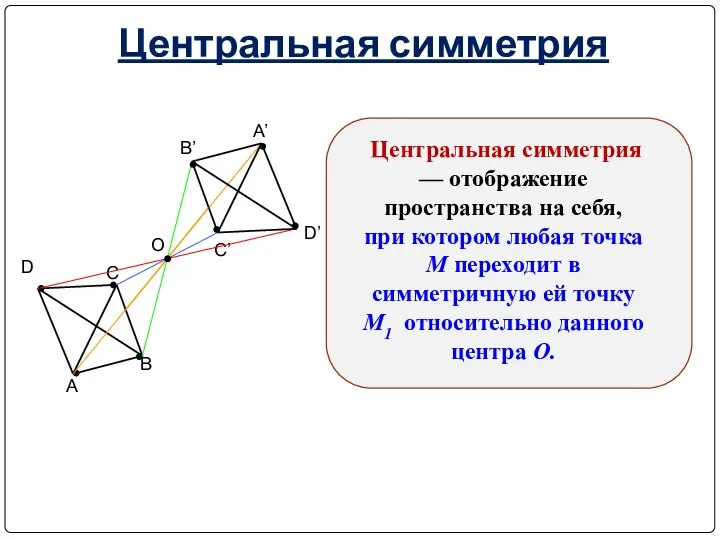
Центральная симметрия
Центральная симметрия — отображение пространства на себя, при котором любая точка М переходит в симметричную ей точку М1 относительно данного центра О.

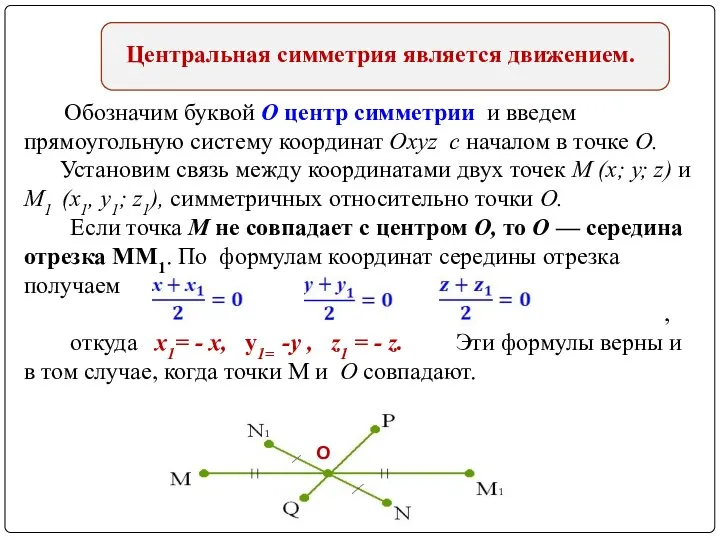
Центральная симметрия является движением.
Обозначим буквой О центр симметрии и введем прямоугольную систему координат Oxyz с началом в точке О. Установим связь между координатами двух точек М (х; у; z) и М1 (х1, у1; z1), симметричных относительно точки О.
Если точка М не совпадает с центром О, то О — середина отрезка ММ1. По формулам координат середины отрезка получаем
,
откуда х1= - х, у1= -у , z1 = - z. Эти формулы верны и в том случае, когда точки M и О совпадают.
О

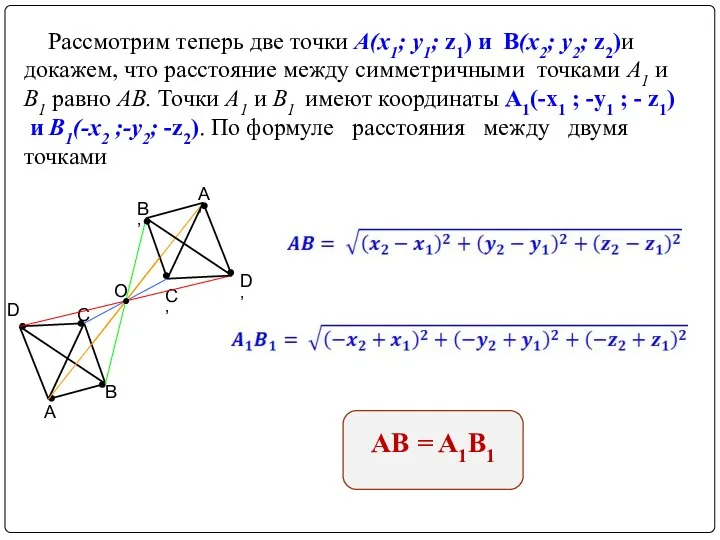
Рассмотрим теперь две точки А(х1; у1; z1) и В(х2; у2; z2)и докажем, что расстояние между симметричными точками А1 и В1 равно АВ. Точки А1 и В1 имеют координаты А1(-х1 ; -у1 ; - z1)
и В1(-х2 ;-у2; -z2). По формуле расстояния между двумя точками
AB = A1B1

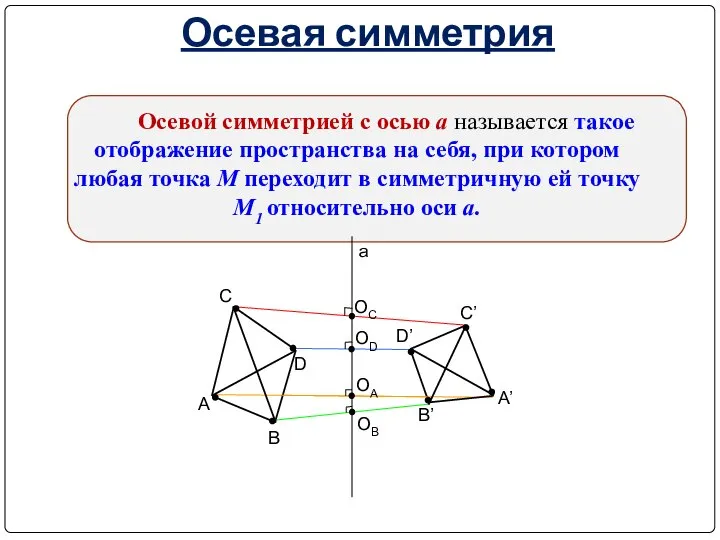
Осевая симметрия
Осевой симметрией с осью а называется такое отображение пространства на себя, при котором любая точка М переходит в симметричную ей точку М1 относительно оси а.

Осевая симметрия является движением.
Для этого введем прямоугольную систему координат Oxyz так, чтобы ось Oz совпала с осью симметрии, и установим связь между координатами двух точек М(х; у; z) и М1(х1, y1; z1), симметричных относительно оси Oz.
Если точка М не лежит на оси Oz , то ось Oz: 1) проходит через середину отрезка ММ1 и 2) перпендикулярна к нему.
Из первого условия по формулам для координат середины отрезка получаем ,
откуда х1= -х и у1 = -у.
Второе условие означает, что аппликаты точек М и М1 равны: z1= z2. Полученные формулы верны и в том случае, когда точка М лежит на оси Oz.

Рассмотрим теперь любые две точки A(х1; у1; z1) и
В(х2; у2; z2) и докажем, что расстояние между симметричными им точками А1 и В1равно АВ.
Точки А1 и В1 имеют координаты А1(-х1 ; -у1 ; - z1) и В1(-х2; -у2; -z2).
По формуле расстояния между двумя
точками находим:
AB = A1B1

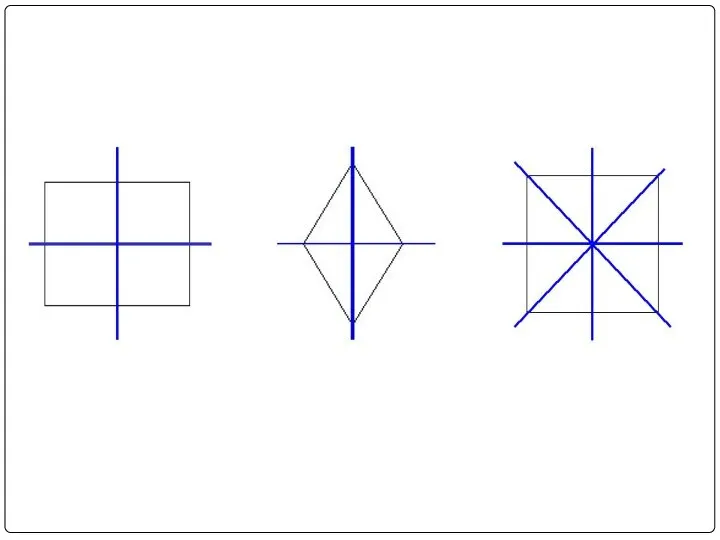
Осевая симметрия

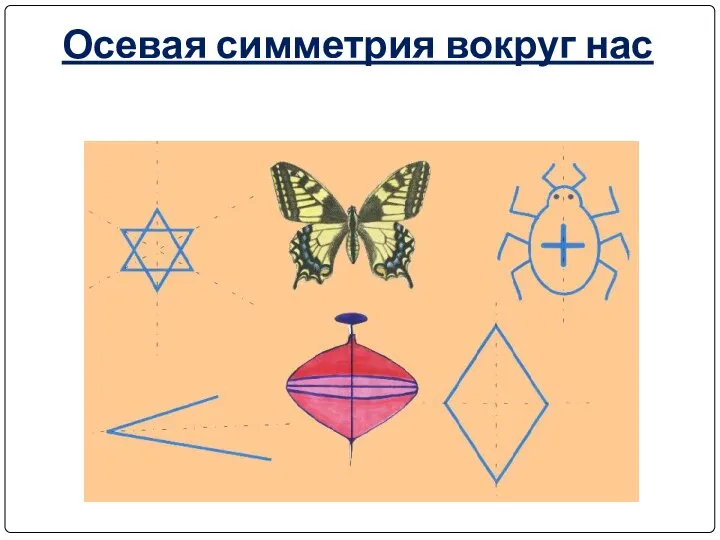
Осевая симметрия вокруг нас

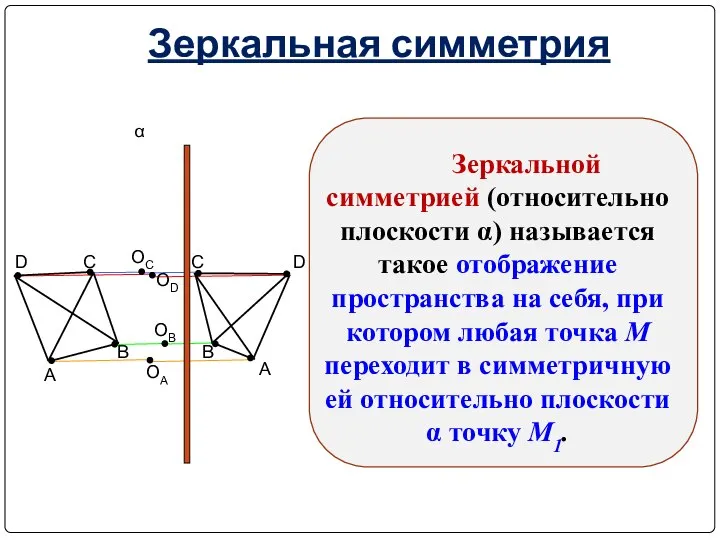
Зеркальная симметрия
Зеркальной симметрией (относительно плоскости α) называется такое отображение пространства на себя, при котором любая точка М переходит в симметричную ей относительно плоскости α точку М1.

Зеркальная симметрия является движением.
Для этого введем прямоугольную систему координат Oxyz так, чтобы плоскость Оху совпала с плоскостью симметрии, и установим связь между координатами двух точек М(х; у;z) и М1(х1; у1; z1), симметричных относительно плоскости Оху.
Если точка М не лежит в плоскости Оху, то эта плоскость:
1) проходит через середину
отрезка ММ1 ;
2) перпендикулярна к нему.
М
К
К
α
МК=М1К1
М1
К1

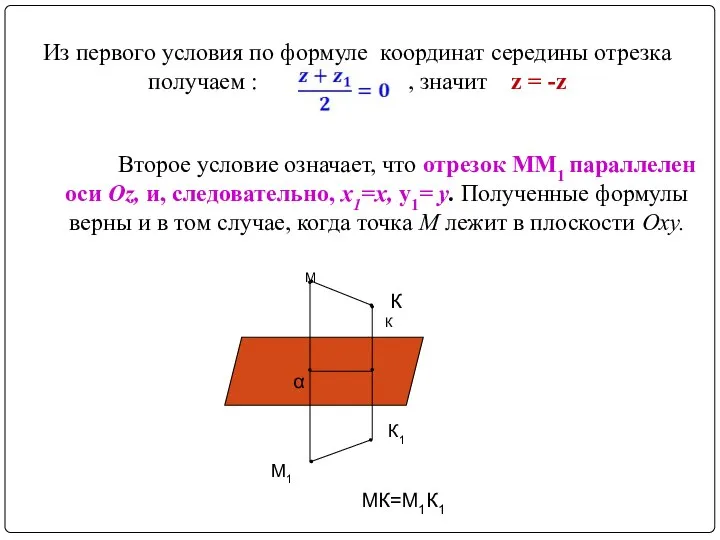
Из первого условия по формуле координат середины отрезка получаем : , значит z = -z
Второе условие означает, что отрезок ММ1 параллелен оси Oz, и, следовательно, х1=х, у1= у. Полученные формулы верны и в том случае, когда точка М лежит в плоскости Оху.
М
К
К
α
МК=М1К1
М1
К1

Рассмотрим теперь две точки А(x1, у1; z1) и В (х2; у2; z2) и докажем, что расстояние между симмеричными им точками А1 и В1 равно АВ. Точки А1 и В1 имеют координаты А1(х1 ; у1 ; - z1) и В1(х2; у2; -z2). По формуле расстояния между двумя точками находим:
AB = A1B1

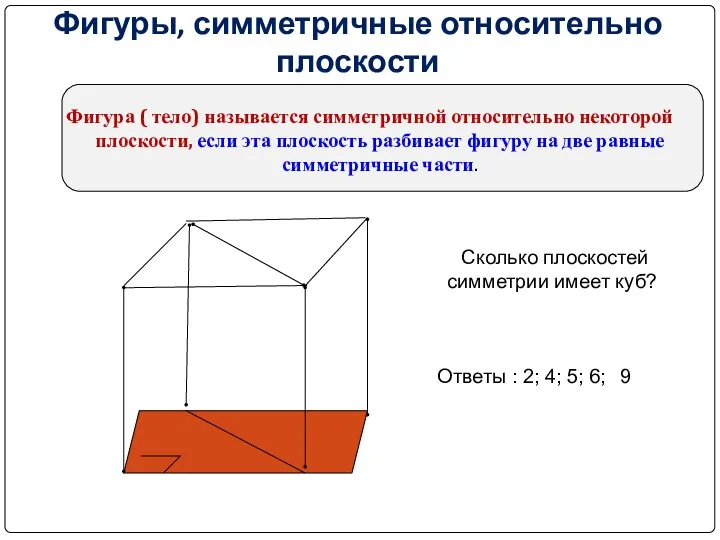
Фигуры, симметричные относительно плоскости
Фигура ( тело) называется симметричной относительно некоторой плоскости, если эта плоскость разбивает фигуру на две равные симметричные части.
Сколько плоскостей симметрии имеет куб?
Ответы : 2; 4; 5; 6;
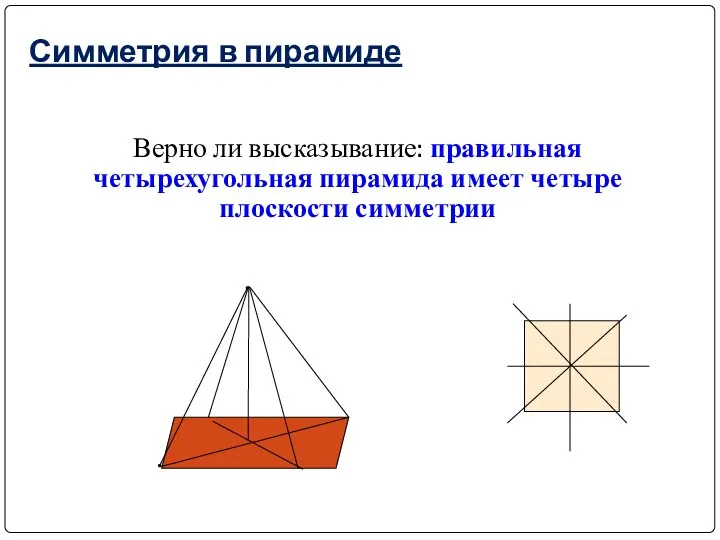
9

Симметрия в пирамиде
Верно ли высказывание: правильная четырехугольная пирамида имеет четыре плоскости симметрии

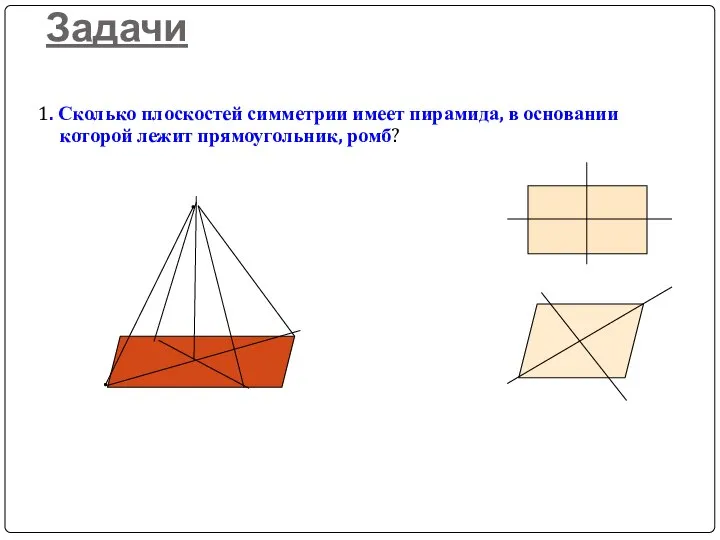
Задачи
1. Сколько плоскостей симметрии имеет пирамида, в основании которой лежит прямоугольник, ромб?

Зеркальная симметрия в архитектуре г. Санкт- Петербурга
Александринский театр
Исаакиевский собор

Улица России
имеет плоскость симметрии в общем обзоре, но не все детали в архитектуре зданий симметричны.

Зеркальная симметрия

Пример зеркальной симметрии
Центральный зал станции

Зеркально симметричные объекты
Осевая симметрия
Зеркальная симметрия
Центральная симметрия

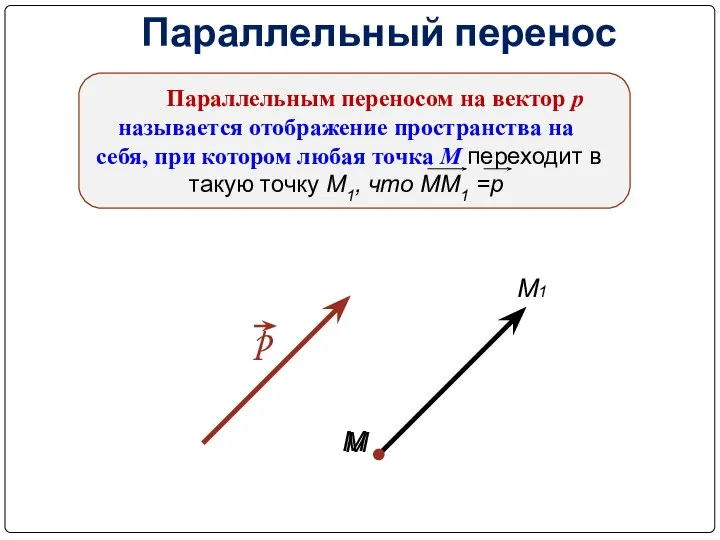
Параллельный перенос
Параллельным переносом на вектор р называется отображение пространства на себя, при котором любая точка М переходит в такую точку М1, что ММ1 =р
М
М1
М

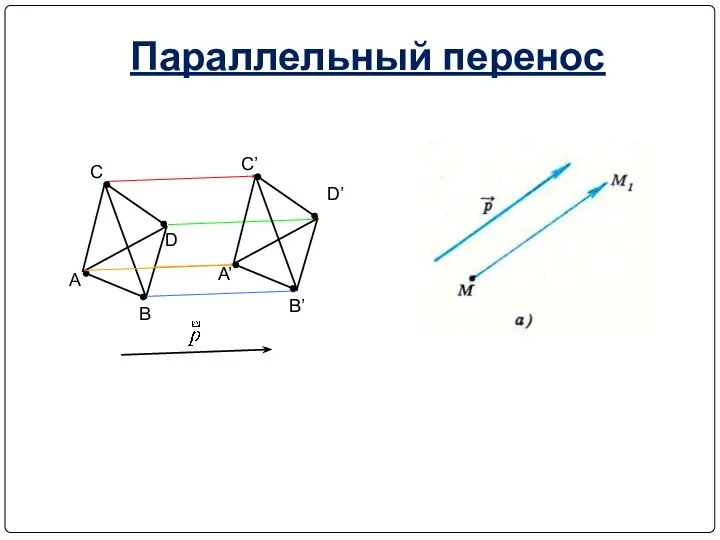
A
B
C
D
A’
B’
C’
D’
Параллельный перенос

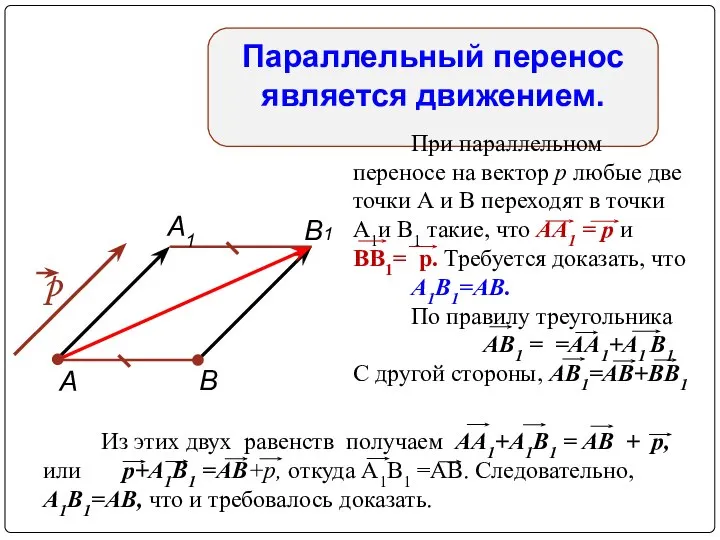
Из этих двух равенств получаем АА1+А1В1 = AВ + p, или р+А1В1 =АВ+p, откуда А1B1 =АВ. Следовательно, А1В1=АВ, что и требовалось доказать.
Параллельный перенос является движением.
При параллельном переносе на вектор р любые две точки А и В переходят в точки А1и В1 такие, что АА1 = р и BB1= р. Требуется доказать, что
А1В1=АВ.
По правилу треугольника
АВ1 = =АА1+А1 В1 C другой стороны, АВ1=АВ+ВВ1
B1
В

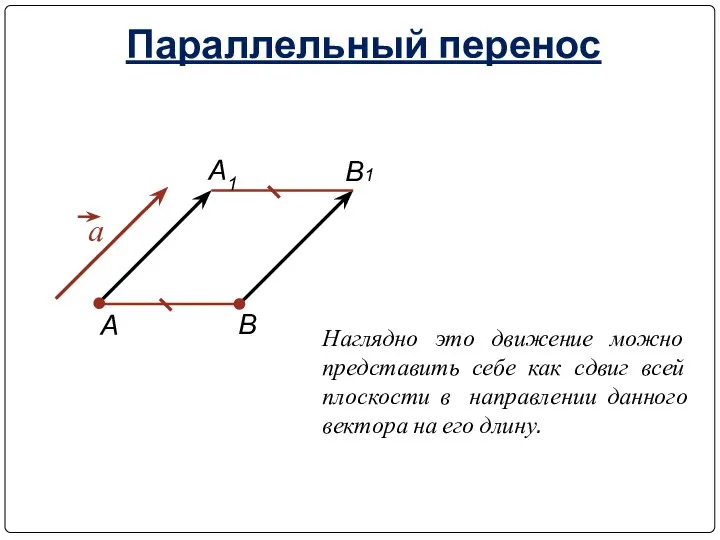
Параллельный перенос
Наглядно это движение можно представить себе как сдвиг всей плоскости в направлении данного вектора на его длину.
B1
В

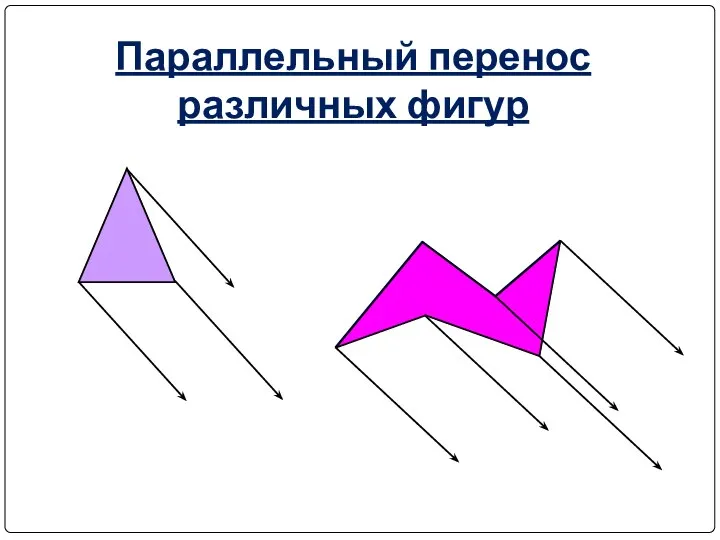
Параллельный перенос различных фигур

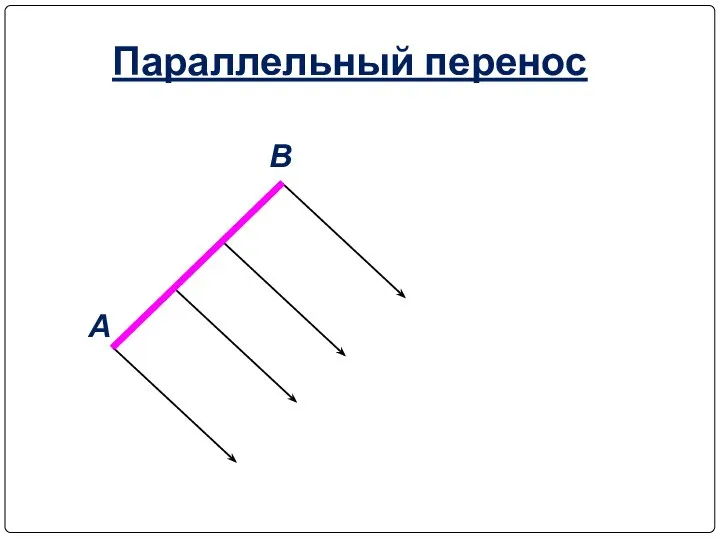
Параллельный перенос
А
В

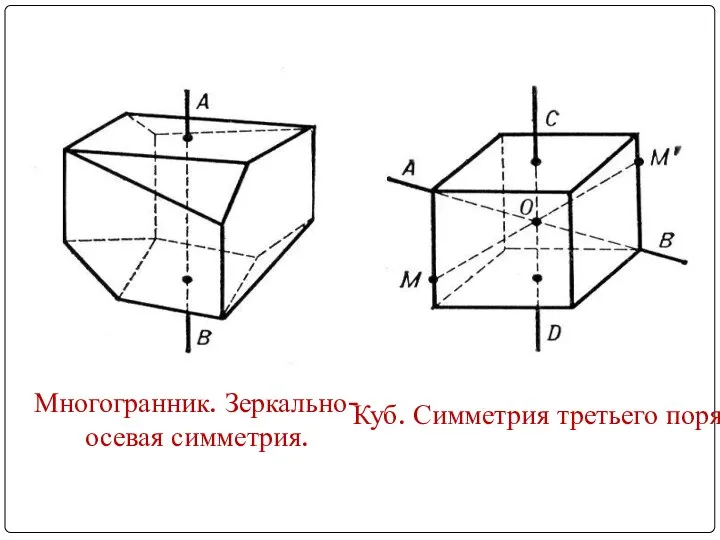
Многогранник. Зеркально-осевая симметрия.
Куб. Симметрия третьего порядка.

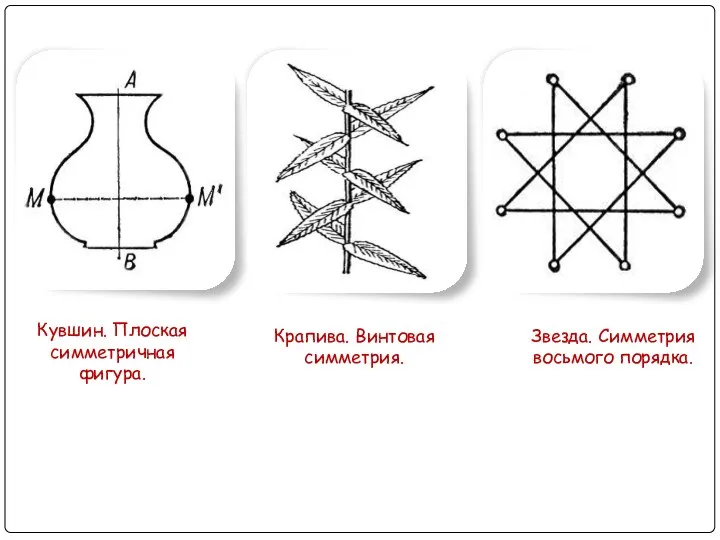
Кувшин. Плоская
симметричная фигура.
Крапива. Винтовая
симметрия.
Звезда. Симметрия
восьмого порядка.

Зеркальная симметрия в природе

Зеркальная симметрия в природе