Слайд 2Тригономе́трия (от греч. τρίγονο (треугольник) и греч. μετρειν (измерять),
то есть измерение треугольников)

— раздел математики,
в котором изучаются тригонометрические функции и их приложения к геометрии.
Данный термин впервые появился в 1595 г. как название книги немецкого математика Бартоломеуса Питискуса (Bartholomäus Pitiscus, 1561—1613),
а сама наука ещё в глубокой древности использовалась для расчётов в астрономии, геодезии и архитектуре.
Слайд 3а
в
с
Синус острого угла в прямоугольном треугольнике — отношение противолежащего катета к гипотенузе.
Косинус

— отношение прилежащего катета к гипотенузе.
Тангенс — отношение противолежащего катета к прилежащему.
Котангенс - отношение прилежащего катета к прилежащему
Слайд 4В XVIII веке Леонард Эйлер дал современные, более общие определения, расширив область

определения этих функций на всю числовую ось.
Слайд 6Р(1; 0)
Р(1; 0)
Поворот точки на угол
Mх
My
M
Mх
My
M

Слайд 7Определение синуса и косинуса угла
Р(1; 0)
M
Ось абсцисс также называют осью косинусов, а

ось ординат осью синусов
Слайд 8Заполним таблицу значений синусов и косинусов
для основных углов

Слайд 9
Определение тангенса и котангенса угла

Слайд 10Заполним таблицу значений синусов и косинусов
для основных углов

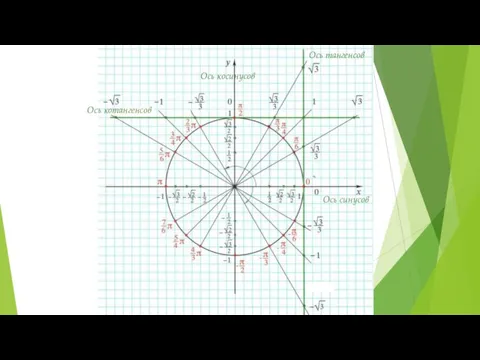
Слайд 11Ось котангенсов
Ось тангенсов
Ось синусов
Ось косинусов










 Прогрессия. Алгебраический анзац
Прогрессия. Алгебраический анзац Упрощение выражений. Решение задач
Упрощение выражений. Решение задач Статистическая теория радиотехнических систем. Корреляционный анализ детерминированных процессов. (Лекция 4)
Статистическая теория радиотехнических систем. Корреляционный анализ детерминированных процессов. (Лекция 4) Знаки тригонометрических функций. Формулы сложения
Знаки тригонометрических функций. Формулы сложения Мнимые числа. Определение комплексных чисел
Мнимые числа. Определение комплексных чисел Линейные неравенства с параметром
Линейные неравенства с параметром Понятие логарифма
Понятие логарифма Решение примеров
Решение примеров Основные результаты ЕГЭ по математике в 2021 году
Основные результаты ЕГЭ по математике в 2021 году Тест. Реши. И ты станешь уважать себя
Тест. Реши. И ты станешь уважать себя Симметрия. Виды симметрии
Симметрия. Виды симметрии Многоугольники в нашей жизни
Многоугольники в нашей жизни День таблицы умножения
День таблицы умножения Реляционная алгебра
Реляционная алгебра Построение графика функции, используя её свойства
Построение графика функции, используя её свойства Интерактивный тренажер Подобные слагаемые
Интерактивный тренажер Подобные слагаемые Таблица умножения числа 2 и на число 2
Таблица умножения числа 2 и на число 2 Презентация на тему Тригонометрические функции
Презентация на тему Тригонометрические функции  Иррациональные неравенства
Иррациональные неравенства Контрольная 2
Контрольная 2 Магические цифры
Магические цифры Подготовка к дифференцированному зачёту по математике. Нижегородский авиационный технический колледж
Подготовка к дифференцированному зачёту по математике. Нижегородский авиационный технический колледж Приемы решения целых уравнений
Приемы решения целых уравнений Презентация на тему Занимательная математика для детей (устный счёт + учимся писать цифры)
Презентация на тему Занимательная математика для детей (устный счёт + учимся писать цифры)  Презентация на тему Квадратный корень. Арифметический квадратный корень
Презентация на тему Квадратный корень. Арифметический квадратный корень  Математические методы решения задач по акустике волнового уравнения. Фундаментальные решения волновых уравнений
Математические методы решения задач по акустике волнового уравнения. Фундаментальные решения волновых уравнений РўР’РёРњРЎ_Лекция 2_Теоремы Рѕ вероятностях СЃРожных событий (4)
РўР’РёРњРЎ_Лекция 2_Теоремы Рѕ вероятностях СЃРожных событий (4) Объемы тел. Подготовка к контрольной работе
Объемы тел. Подготовка к контрольной работе