Обработка результатов измерений при прямых однократных измерениях. Математические методы планирования активного эксперимента
- Главная
- Математика
- Обработка результатов измерений при прямых однократных измерениях. Математические методы планирования активного эксперимента

Содержание
- 2. 1. Обработка результатов наблюдений при прямых однократных измерениях. Прямые однократные измерения имеют наибольшее распространение в измерительной
- 9. 2. Математические методы планирования и анализа активного эксперимента. Обработку результатов активного эксперимента осуществляют на основе регрессионного
- 10. 2.1. Проверка гипотезы о нормальном законе распределения погрешностей эксперимента. Существует несколько способов проверки гипотезы о нормальном
- 13. 3. Проверка гипотезы о воспроизводимости опытов. 3.1. Проверка гипотезы о воспроизводимости с помощью критерия Кочрена. Для
- 21. Скачать презентацию
Слайд 21. Обработка результатов наблюдений при прямых однократных измерениях.
Прямые однократные измерения имеют наибольшее
1. Обработка результатов наблюдений при прямых однократных измерениях.
Прямые однократные измерения имеют наибольшее

распространение в измерительной технике, быту, медицинской практике проведения биохимических анализов с целью постановки предварительного анализа и во всех случаях, где однократное измерение может дать представление об измеряемой величине.
При однократных измерениях показание приборы xi принимают равным результату измерения, при этом трудоемкость и время измерения существенно уменьшаются.
Однократные измерения с точки зрения соотношения случайных и систематических погрешностей целесообразны тогда, когда сходимость результатов измерений высока, а появление систематической погрешности неизбежно.
Таким образом, однократные измерения применимы в том случае, если среднее квадратичное отклонение СКО результатов наблюдений, выполненных в одинаковых условиях (а именно СКО является параметром сходимости) близко к нулю.
При однократных измерениях показание приборы xi принимают равным результату измерения, при этом трудоемкость и время измерения существенно уменьшаются.
Однократные измерения с точки зрения соотношения случайных и систематических погрешностей целесообразны тогда, когда сходимость результатов измерений высока, а появление систематической погрешности неизбежно.
Таким образом, однократные измерения применимы в том случае, если среднее квадратичное отклонение СКО результатов наблюдений, выполненных в одинаковых условиях (а именно СКО является параметром сходимости) близко к нулю.
Слайд 92. Математические методы планирования и анализа активного эксперимента.
Обработку результатов активного эксперимента осуществляют
2. Математические методы планирования и анализа активного эксперимента.
Обработку результатов активного эксперимента осуществляют

на основе регрессионного анализа. Для использования регрессионного анализа необходимы следующие предпосылки:
а) ошибки эксперимента должны быть распределены по нормальному закону;
б) опыты должны быть воспроизводимы.
Следовательно, перед выполнением активного эксперимента необходимо провести предварительные серии опытов на изучаемом объекте, чтобы выявить наличие или отсутствие этих предпосылок.
а) ошибки эксперимента должны быть распределены по нормальному закону;
б) опыты должны быть воспроизводимы.
Следовательно, перед выполнением активного эксперимента необходимо провести предварительные серии опытов на изучаемом объекте, чтобы выявить наличие или отсутствие этих предпосылок.
Слайд 10 2.1. Проверка гипотезы о нормальном законе распределения погрешностей эксперимента.
Существует несколько способов
2.1. Проверка гипотезы о нормальном законе распределения погрешностей эксперимента.
Существует несколько способов

проверки гипотезы о нормальном законе распределения ошибок эксперимента. Для этой цели часто используют W -критерий. Статический критерий W (критерий согласия Шапиро-Уилка) предназначен для двух статических моделей (нормальной и экспоненциальной). Он является более мощным, т. е. обеспечивает большую вероятность исключить неправильную гипотезу (модуль) по сравнению с критерием χ2 (хи-квадрат). В таком случае требуется от 3 до 50 параллельных опытов, выполненных в одинаковых условиях.
Проверка нулевой гипотезы о принадлежности неизвестного экспериментального закона распределения погрешностей эксперимента теоретическому нормальному закону осуществляется в следующей последовательности:
а) результаты опытов располагают в виде неубывающей последовательности:
y1 ≤ y2 ≤ y3 ≤ …≤ yk ,
где k – число параллельных опытов;
Проверка нулевой гипотезы о принадлежности неизвестного экспериментального закона распределения погрешностей эксперимента теоретическому нормальному закону осуществляется в следующей последовательности:
а) результаты опытов располагают в виде неубывающей последовательности:
y1 ≤ y2 ≤ y3 ≤ …≤ yk ,
где k – число параллельных опытов;
Слайд 133. Проверка гипотезы о воспроизводимости опытов.
3.1. Проверка гипотезы о воспроизводимости с помощью
3. Проверка гипотезы о воспроизводимости опытов.
3.1. Проверка гипотезы о воспроизводимости с помощью

критерия Кочрена.
Для проверки гипотезы о принадлежности двух выборочных дисперсий одной генеральной совокупности (их однородности), а, следовательно, и равноточности серий измерений (показатель воспроизводимости опытов в эксперименте) используется критерий Кочрена.
Для проверки гипотезы с помощью критерия Кочрена необходимы результаты нескольких серий параллельных опытов. В каждой из них количество опытов должно быть одинаково. Обычно число серий не велико — 2 ÷ 3. Количество опытов в серии также может быть небольшим — 2 ÷ 3.
Результаты эксперимента помещают в таблицу 2.
Для проверки гипотезы о принадлежности двух выборочных дисперсий одной генеральной совокупности (их однородности), а, следовательно, и равноточности серий измерений (показатель воспроизводимости опытов в эксперименте) используется критерий Кочрена.
Для проверки гипотезы с помощью критерия Кочрена необходимы результаты нескольких серий параллельных опытов. В каждой из них количество опытов должно быть одинаково. Обычно число серий не велико — 2 ÷ 3. Количество опытов в серии также может быть небольшим — 2 ÷ 3.
Результаты эксперимента помещают в таблицу 2.








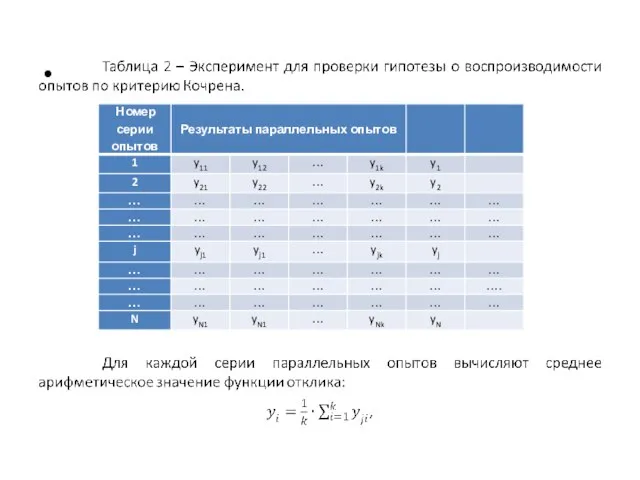





 Метод морфологического анализа
Метод морфологического анализа Worksheet 3 (reatke)
Worksheet 3 (reatke) Подготовка к ОГЭ по математике
Подготовка к ОГЭ по математике Задания Кириллу
Задания Кириллу Решение систем линейных уравнений методом Гаусса
Решение систем линейных уравнений методом Гаусса Использование деревьев при решении алгоритмических задач
Использование деревьев при решении алгоритмических задач Признаки равенства треугольников. Равнобедренный треугольник
Признаки равенства треугольников. Равнобедренный треугольник Математические компоненты вычитания
Математические компоненты вычитания Таблицы и диаграммы
Таблицы и диаграммы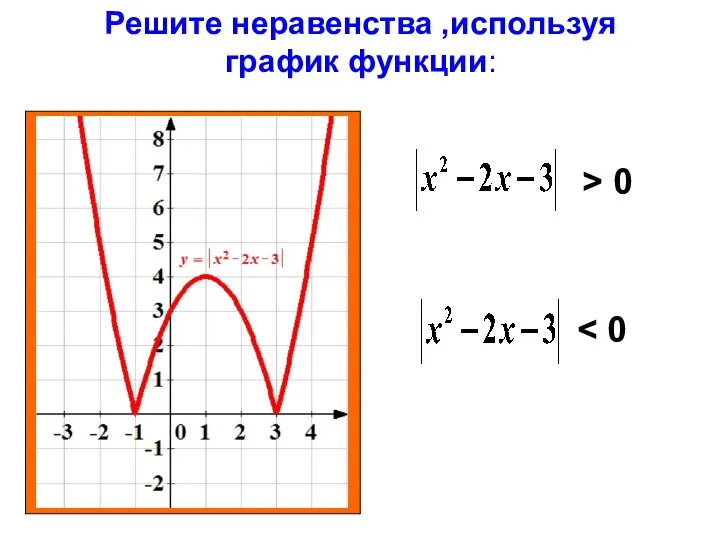 Решите неравенства ,используя график функции: x 2x 3 > 0
Решите неравенства ,используя график функции: x 2x 3 > 0 Призмы и антипризмы
Призмы и антипризмы Натуральные числа. Обобщающий урок
Натуральные числа. Обобщающий урок Квадратные уравнения
Квадратные уравнения Основные формулы
Основные формулы Дидактическая игра. Веселый ёжик
Дидактическая игра. Веселый ёжик Естественный отбор. Бинарный урок по биологии и математике (часть 3)
Естественный отбор. Бинарный урок по биологии и математике (часть 3) Элементы аналитической геометрии на плоскости
Элементы аналитической геометрии на плоскости Формулы для нахождения площади треугольника
Формулы для нахождения площади треугольника VIII Международная олимпиада по математике для I курсов ССУЗ
VIII Международная олимпиада по математике для I курсов ССУЗ dispersionnyy-analiz(1)
dispersionnyy-analiz(1) Признаки равенства треугольников
Признаки равенства треугольников Признак существования определенного интеграла. Лекция №7
Признак существования определенного интеграла. Лекция №7 Решите уравнение (вариант 26 )
Решите уравнение (вариант 26 ) Вычитание натуральных чисел
Вычитание натуральных чисел Геометрические фигуры вокруг нас
Геометрические фигуры вокруг нас Презентация на тему Магия Чисел
Презентация на тему Магия Чисел  Перетворення графіків функцій
Перетворення графіків функцій Повторение изученного материала, 1 класс
Повторение изученного материала, 1 класс