08.09

Повторите свойства треугольников:

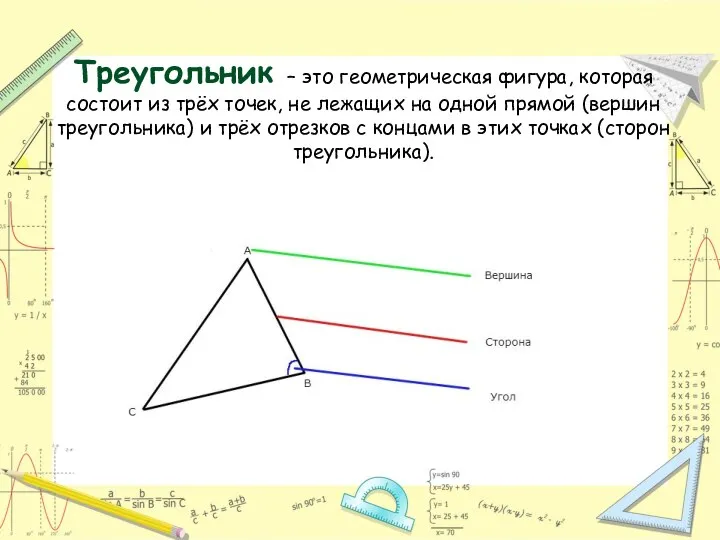
Треугольник – это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой (вершин треугольника) и трёх отрезков с концами в этих точках (сторон треугольника).

Свойства углов треугольника
Сумма углов треугольника равна 180˚.
У любого треугольника хотя бы два угла острые.
Внешний угол треугольника равен сумме двух внутренних, не смежных с ним.

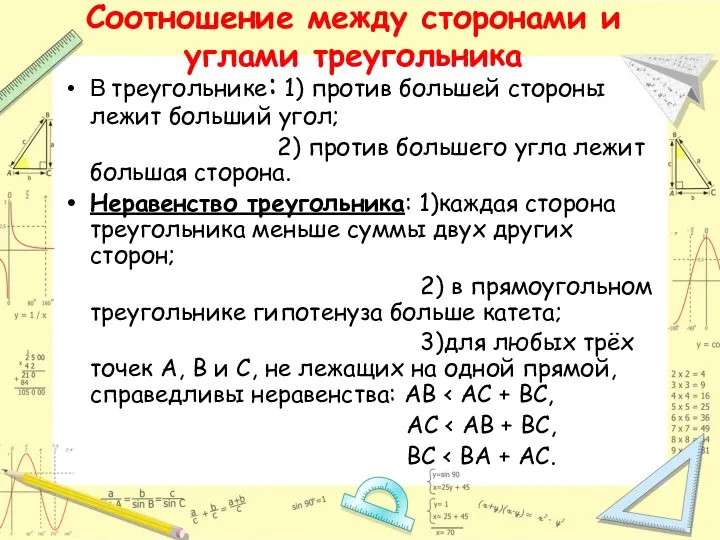
Соотношение между сторонами и углами треугольника
В треугольнике: 1) против большей стороны лежит больший угол;
2) против большего угла лежит большая сторона.
Неравенство треугольника: 1)каждая сторона треугольника меньше суммы двух других сторон;
2) в прямоугольном треугольнике гипотенуза больше катета;
3)для любых трёх точек А, В и С, не лежащих на одной прямой, справедливы неравенства: АВ < АС + ВС,
АС < АВ + ВС,
ВС < ВА + АС.

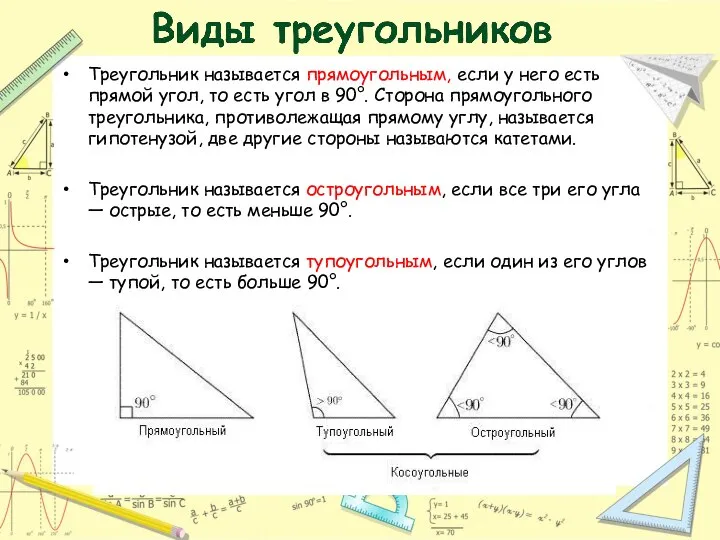
Треугольник называется прямоугольным, если у него есть прямой угол, то есть угол в 90°. Сторона прямоугольного треугольника, противолежащая прямому углу, называется гипотенузой, две другие стороны называются катетами.
Треугольник называется остроугольным, если все три его угла — острые, то есть меньше 90°.
Треугольник называется тупоугольным, если один из его углов — тупой, то есть больше 90°.

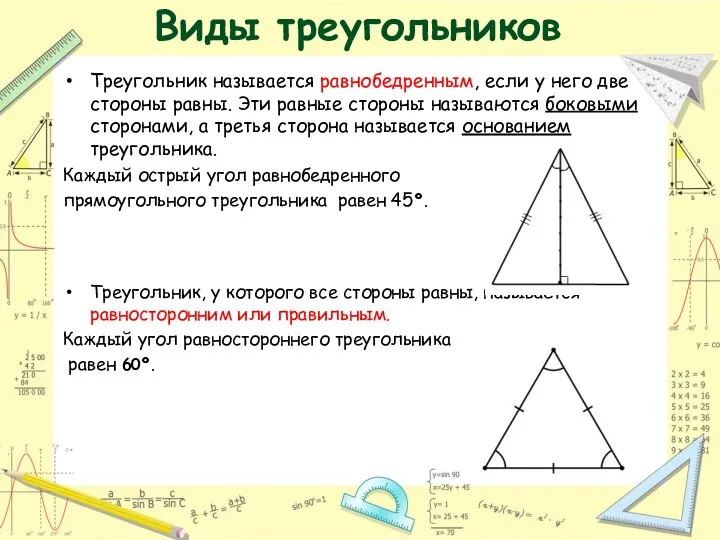
Виды треугольников
Треугольник называется равнобедренным, если у него две стороны равны. Эти равные стороны называются боковыми сторонами, а третья сторона называется основанием треугольника.
Каждый острый угол равнобедренного
прямоугольного треугольника равен 45º.
Треугольник, у которого все стороны равны, называется равносторонним или правильным.
Каждый угол равностороннего треугольника
равен 60º.

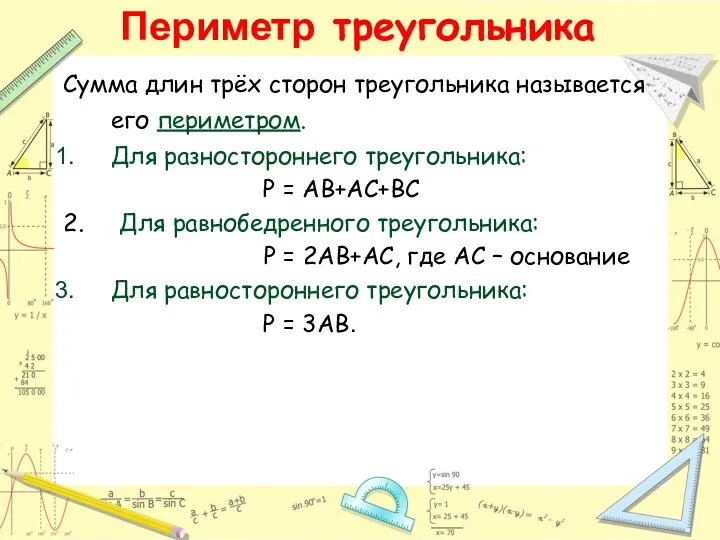
Периметр треугольника
Сумма длин трёх сторон треугольника называется его периметром.
Для разностороннего треугольника: Р = АВ+АС+ВС
2. Для равнобедренного треугольника:
Р = 2АВ+АС, где АС – основание
Для равностороннего треугольника:
Р = 3АВ.

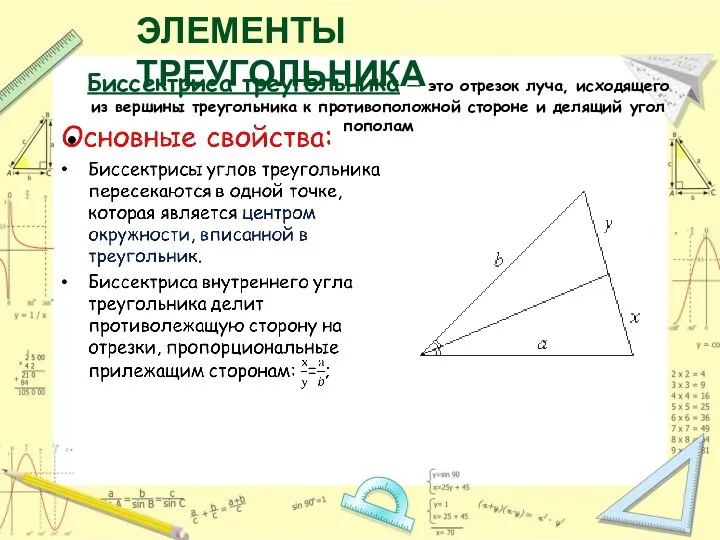
Биссектриса треугольника — это отрезок луча, исходящего из вершины треугольника к противоположной стороне и делящий угол пополам
ЭЛЕМЕНТЫ ТРЕУГОЛЬНИКА

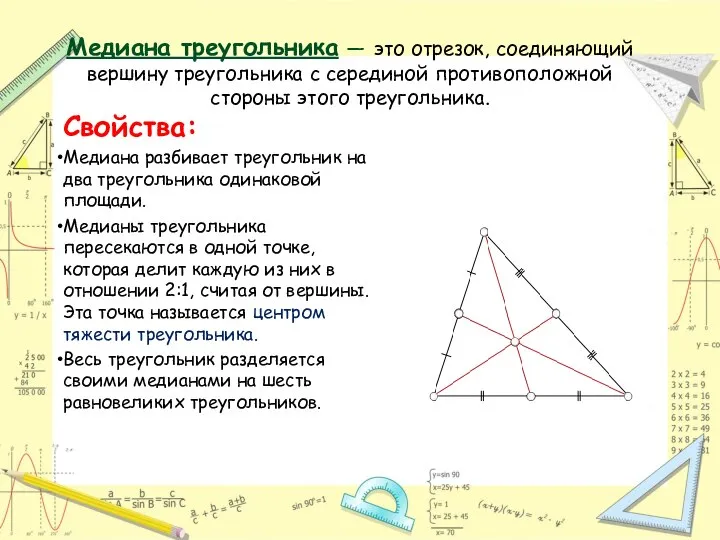
Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны этого треугольника.
Свойства:
Медиана разбивает треугольник на два треугольника одинаковой площади.
Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника.
Весь треугольник разделяется своими медианами на шесть равновеликих треугольников.

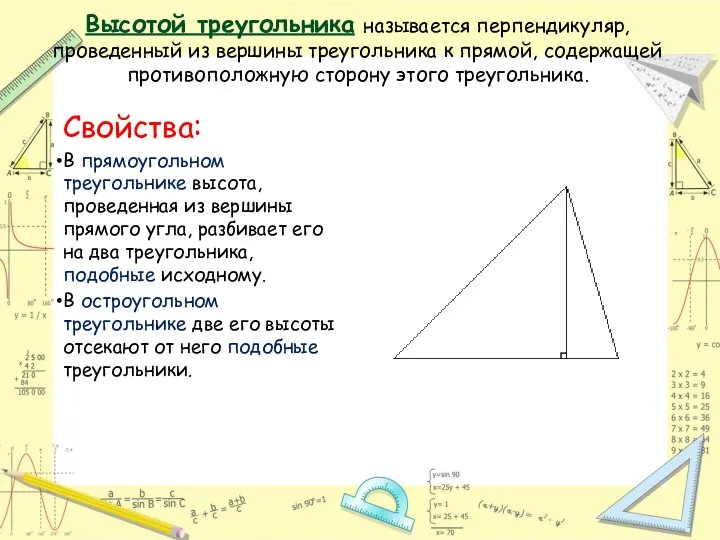
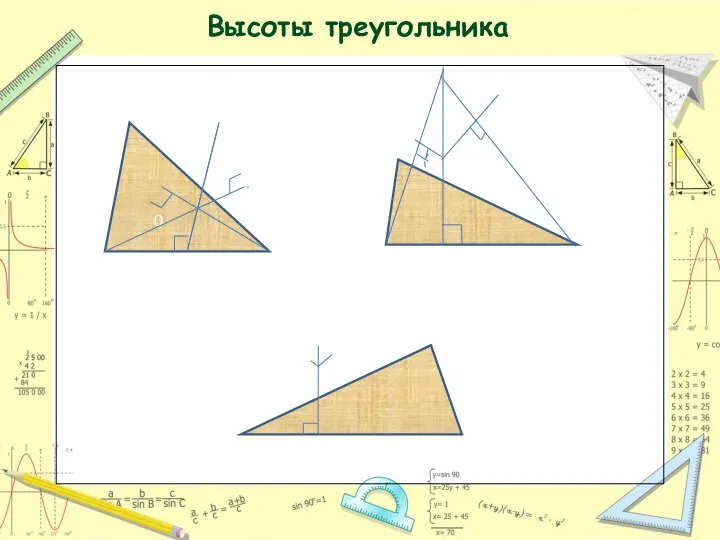
Высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону этого треугольника.
Свойства:
В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобные исходному.
В остроугольном треугольнике две его высоты отсекают от него подобные треугольники.

Высоты треугольника
0

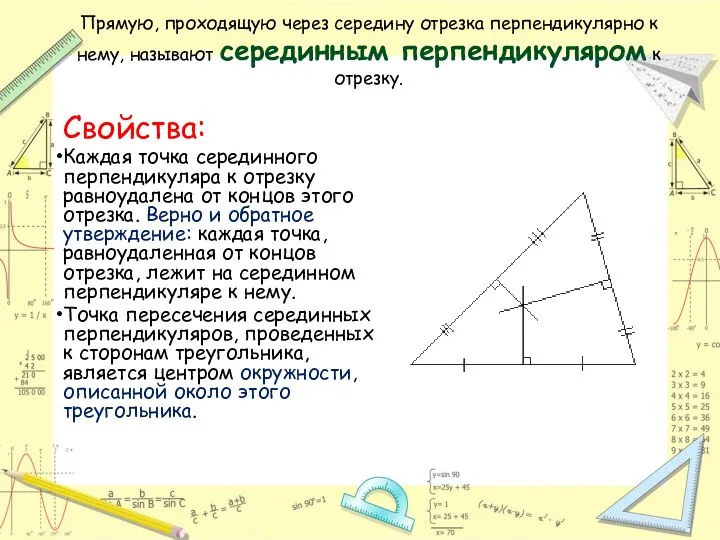
Прямую, проходящую через середину отрезка перпендикулярно к нему, называют серединным перпендикуляром к отрезку.
Свойства:
Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Верно и обратное утверждение: каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.
Точка пересечения серединных перпендикуляров, проведенных к сторонам треугольника, является центром окружности, описанной около этого треугольника.

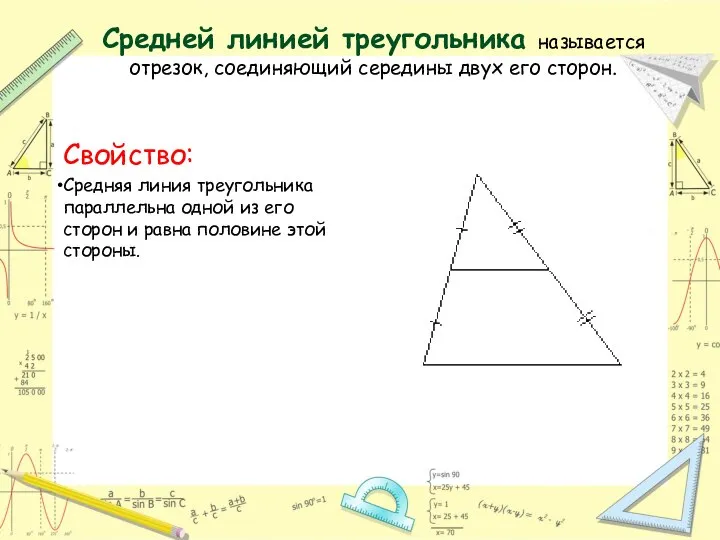
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
Свойство:
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.

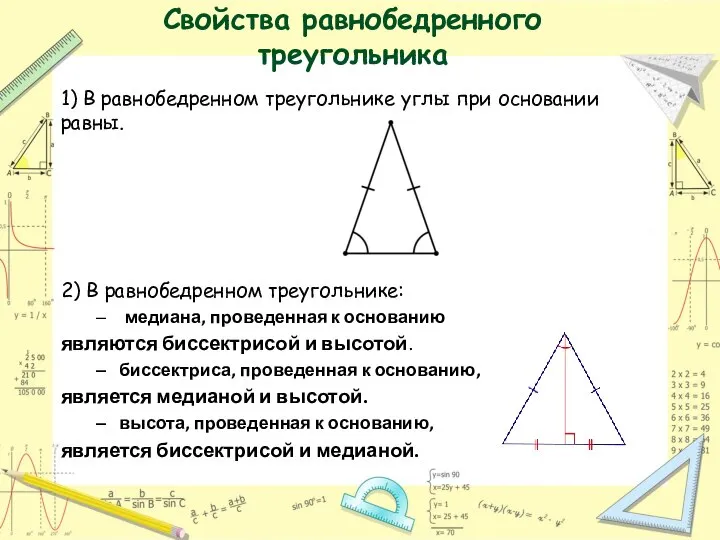
Свойства равнобедренного треугольника
1) В равнобедренном треугольнике углы при основании равны.
2) В равнобедренном треугольнике:
медиана, проведенная к основанию
являются биссектрисой и высотой.
биссектриса, проведенная к основанию,
является медианой и высотой.
высота, проведенная к основанию,
является биссектрисой и медианой.

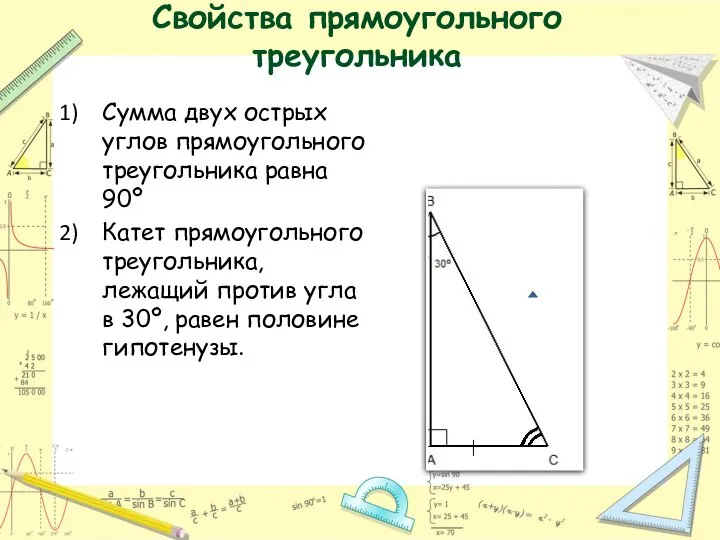
Свойства прямоугольного треугольника
Сумма двух острых углов прямоугольного треугольника равна 90º
Катет прямоугольного треугольника, лежащий против угла в 30º, равен половине гипотенузы.

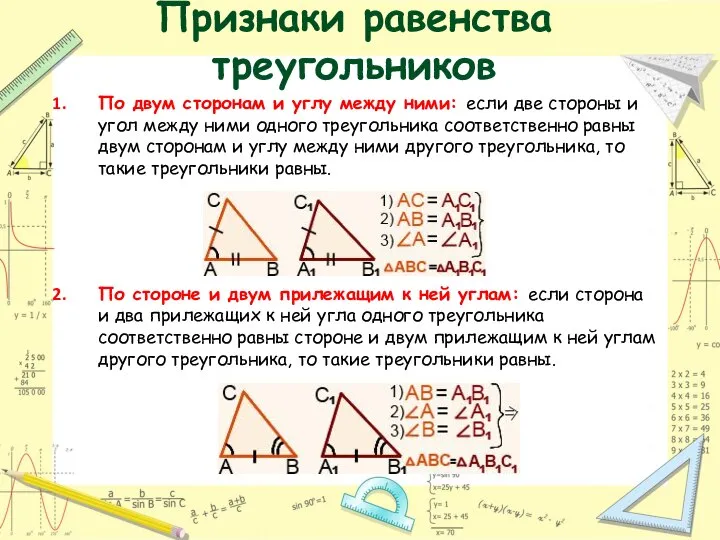
Признаки равенства треугольников
По двум сторонам и углу между ними: если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
По стороне и двум прилежащим к ней углам: если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

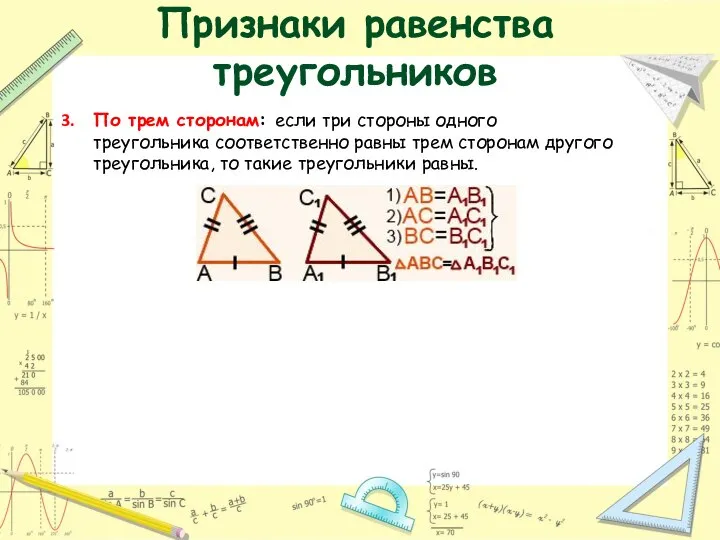
Признаки равенства треугольников
По трем сторонам: если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

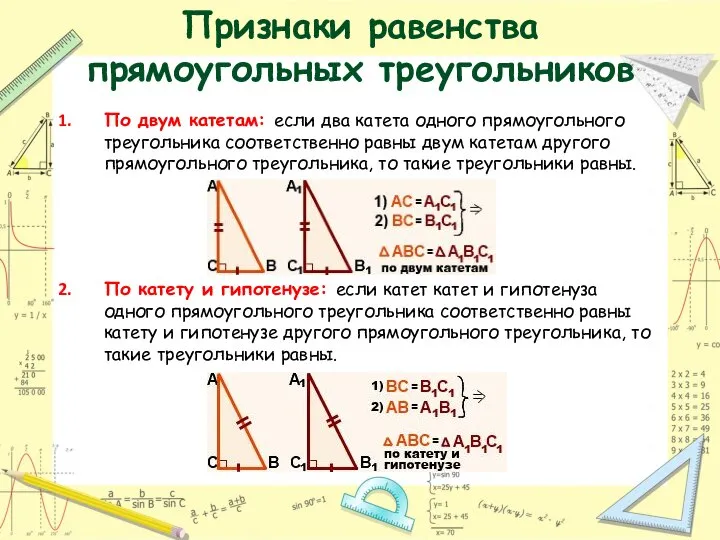
Признаки равенства прямоугольных треугольников
По двум катетам: если два катета одного прямоугольного треугольника соответственно равны двум катетам другого прямоугольного треугольника, то такие треугольники равны.
По катету и гипотенузе: если катет катет и гипотенуза одного прямоугольного треугольника соответственно равны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники равны.

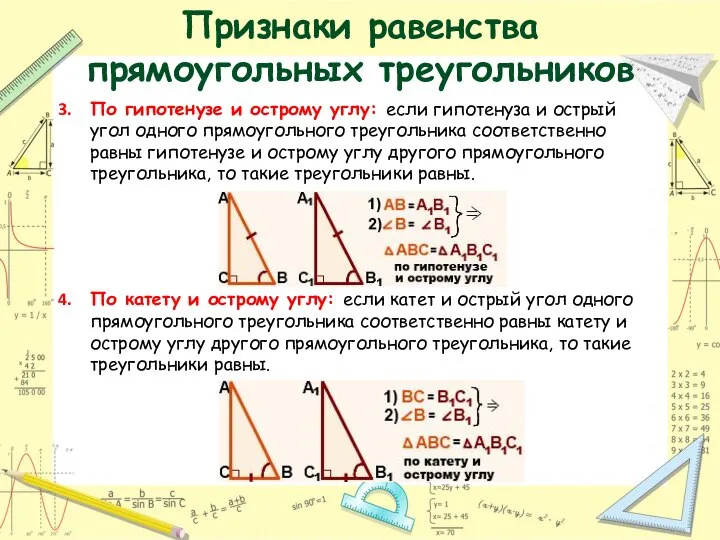
Признаки равенства прямоугольных треугольников
По гипотенузе и острому углу: если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
По катету и острому углу: если катет и острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.

Площадь треугольника
Через сторону и высоту.
Через две стороны и угол между ними.
Через три стороны.

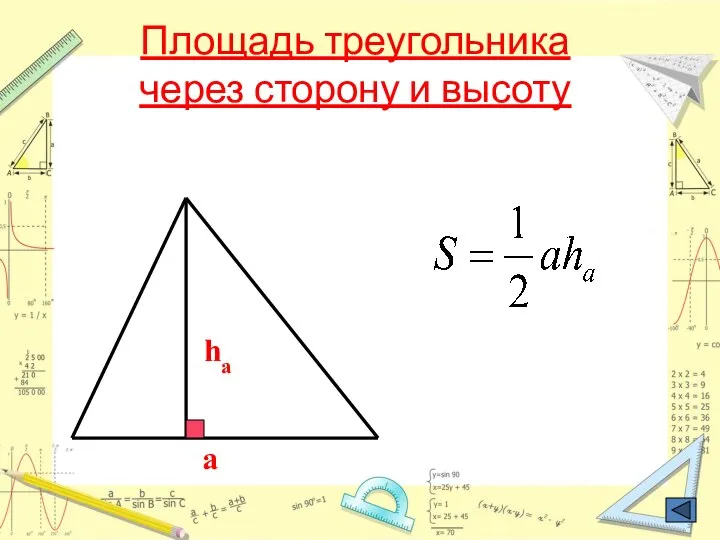
Площадь треугольника
через сторону и высоту
a
ha

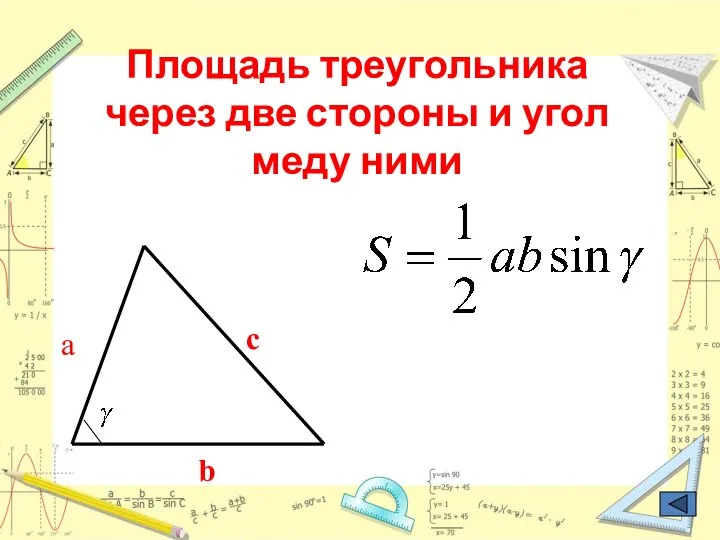
Площадь треугольника
через две стороны и угол меду ними
b
c
a

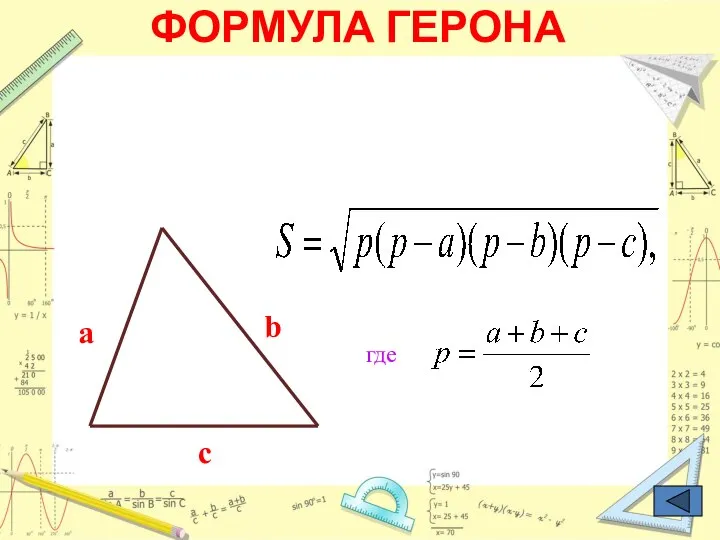
ФОРМУЛА ГЕРОНА
a
b
c
где

Теорема Пифагора
В прямоугольном треугольнике квадрат гипотенузы равен сумме
квадратов катетов.
с² = а² + b²

Обратная теорема
теореме Пифагора
Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный.
AB² = AC² + BC²

В прямоугольнике АВСD найдите ВС, если CD = 1,5 и АС = 2,5
Дано: Решение:
ABCD – прямоуг.
СД = 1,5
АС = 2,5
Найти:
ВС - ?
с² = а² + b²
а² = с² - b²
а² = 6,25 – 2,25
а² = 4
а = 2
Ответ: 2
A
B
C
D
1,5
2,5