Площадь треугольника

Какой треугольник имеет наибольшую площадь?

Гипотеза
Я считаю, что площадь треугольника зависит от длин сторон, от величин углов треугольника.

Цель:
Исследовать зависимость площади треугольника
от размеров его элементов.
Задачи:
1. Изучить зависимость площади треугольника от длины стороны и высоты.
2. Изучить зависимость площади треугольника
от величины его угла.
3. Изучить зависимость площади треугольника
от его вида.

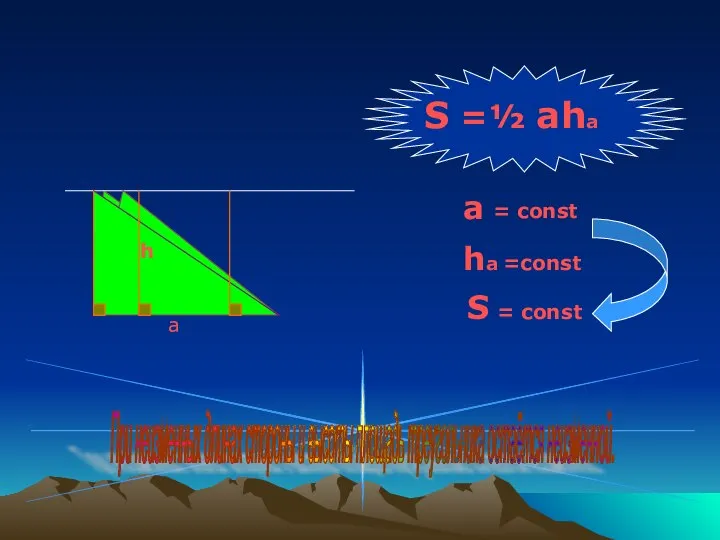
S =½ aha
a
ha
= const
=const
S = const
При неизменных длинах стороны и высоты площадь треугольника остаётся неизменной.
a
h

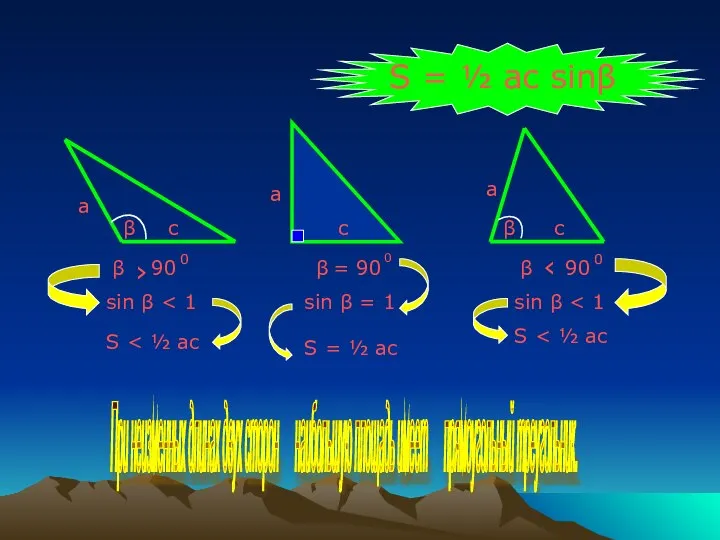
S = ½ ac sinβ
β
β
β
β
β
‹
‹
S < ½ ac
= 90
0
90
90
0
0
sin β = 1
sin β < 1
sin β < 1
S < ½ ac
S = ½ ac
При неизменных длинах двух сторон наибольшую площадь имеет прямоугольный треугольник.
а
а
а
с
с
с

а
h1 < r
h1
h2
h2 < r
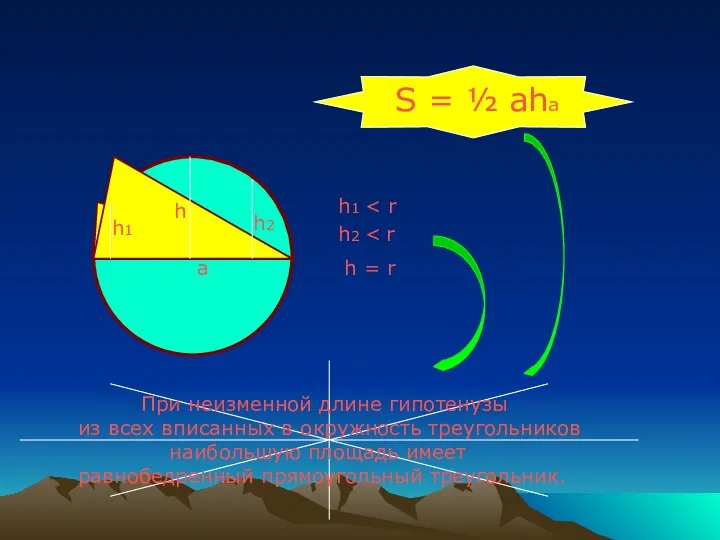
h
h = r
S = ½ aha
При неизменной длине гипотенузы
из всех вписанных в окружность треугольников
наибольшую площадь имеет
равнобедренный прямоугольный треугольник.

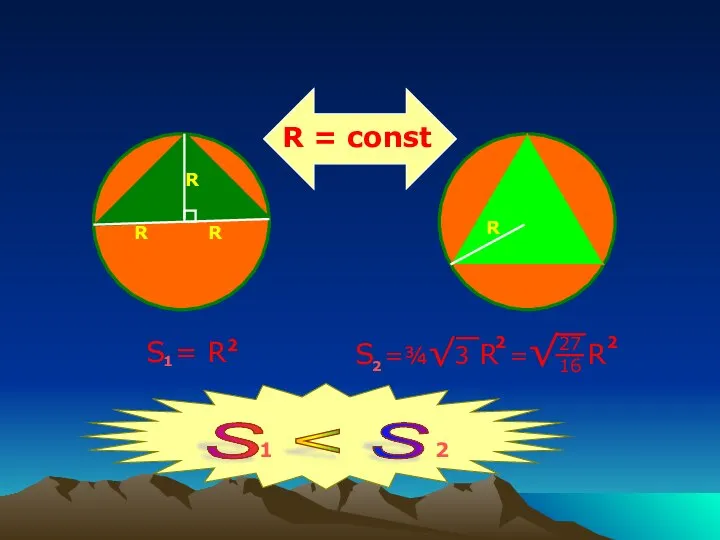
R
R
R
S = R
R = const
S =¾√3 R =√ R
27
16
1
2
S < S
1
2
R
2
2
2

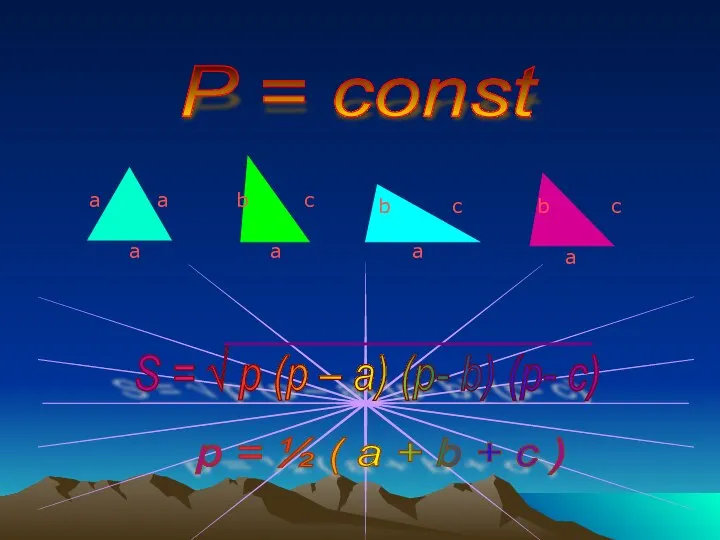
P = const
a
a
a
a
a
a
b
b
b
c
c
c
S = √ p (p – a) (p- b) (p- c)
p = ½ ( a + b + c )

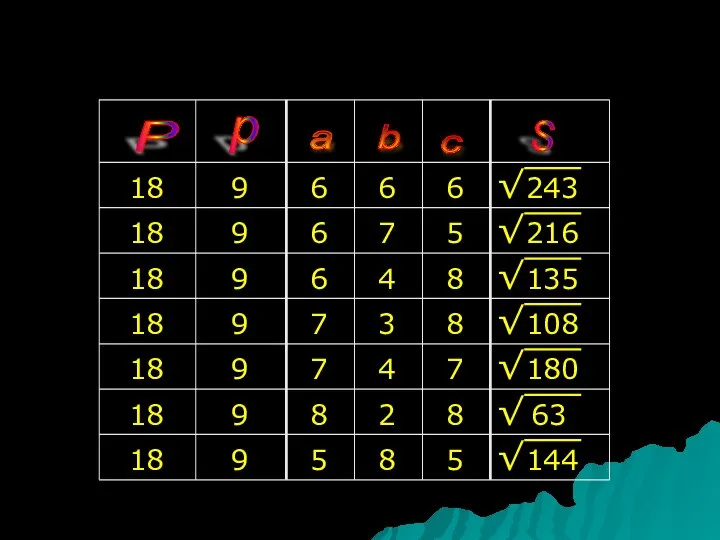
P
p
a
b
c
S
18
18
18
18
18
18
9
9
9
9
9
9
6
6
6
6
6
7
7
18
9
7
7
5
5
5
4
4
8
3
8
8
8
8
2
√
√
√
√
√
√
√
243
216
135
108
180
63
144

Из всех треугольников, имеющих один и тот же периметр, наибольшую
площадь имеет равносторонний треугольник!