- Главная
- Математика
- Кадры, производительность труда, заработная плата

Содержание
- 2. Модификации принципа резолюции (продолжение) Основные вопросы: Лок-резолюция 2. Линейная резолюция 3. OL-резолюция 4. Входная резолюция и
- 3. Введем следующую индексацию: P1∨Q2, P3∨¬Q4, ¬P6∨Q5, ¬P8∨¬Q7 Из дизъюнктов 1-4 можно получить только одну лок-резольвенту (5)
- 4. Линейная резолюция Линейная резолюция довольно легко может быть реализована на ЭВМ, обладает простой структурой и полнотой.
- 5. Рис. 1.
- 6. П р и м е р 1 . Пусть S = {P ∨ Q, ¬P ∨
- 7. Рис. 2.
- 8. 2. OL-резолюция Линейная резолюция может быть существенно усилена введением понятия упорядоченного дизъюнкта и использованием информации о
- 9. Если две или больше литер (с одинаковыми знаками) упорядоченного дизъюнкта С имеют НОУ σ, то упорядоченный
- 10. Отметим, что связывание понятия упорядоченных дизъюнктов с линейной резолюцией не нарушает ее полноты, но существенно увеличивает
- 14. Таким образом, при получении редуцируемого упорядоченного дизъюнкта нет необходимости искать, с каким из полученных ранее дизъюнктов
- 16. Теперь формально определим OL-вывод. Пусть дано множество упорядоченных дизъюнктов S и упорядоченный дизъюнкт С1 из S.
- 17. Следующая теорема устанавливает полноту OL-резолюции (Лавленд, Ковальский, Кюнер). Теорема 2. (о полноте OL-резолюции). Если С является
- 19. или в стандартной форме: 1. ¬C(x) ∨ O(x) ∨ P(f(x)); 2. ¬C(x) ∨ O(x) ∨ S(x,
- 20. Рис. 4.
- 21. Отметим, что OL-вывод успешно конкурирует со многими резолюционными методами вывода за счет простоты организации поиска. Простота
- 22. Входная резолюция проста, эффективна, но в общем случае, к сожалению, как было видно из примера 1,
- 23. П р и м е р (о детективе) . Горничная сказала, что она видела дворецкого в
- 25. Входная резолюция и вывод в языке Пролог В языке Пролог используется упорядоченная входная резолюция, т.е. литеры
- 27. Скачать презентацию
Слайд 2Модификации принципа резолюции (продолжение)
Основные вопросы:
Лок-резолюция
2. Линейная резолюция
3. OL-резолюция
4. Входная резолюция и вывод
Модификации принципа резолюции (продолжение)
Основные вопросы:
Лок-резолюция
2. Линейная резолюция
3. OL-резолюция
4. Входная резолюция и вывод

Лок-резолюция
Идея лок-резолюции состоит в использовании индексов для упорядочения литер в дизъюнктах из данного множества S. После индексации удалять разрешается только литеры с наименьшим индексом в каждом из дизъюнктов. Литера наследует свои индексы из посылок. Если литера наследует более одного индекса, то ей ставится в соответствие наименьший индекс.
Рассмотрим множество S дизъюнктов,
P∨Q, P∨¬Q, ¬P∨Q, ¬P∨¬Q
Введем индексы, которые будем писать справа вверху от литеры:
Слайд 3Введем следующую индексацию:
P1∨Q2,
P3∨¬Q4,
¬P6∨Q5,
¬P8∨¬Q7
Из дизъюнктов 1-4 можно получить
Введем следующую индексацию:
P1∨Q2,
P3∨¬Q4,
¬P6∨Q5,
¬P8∨¬Q7
Из дизъюнктов 1-4 можно получить

(5) ¬P6 - ЛР(3,4)
Из дизъюнктов 1-5 можно получить только две лок-резольвенты
(6) Q2 - ЛР(1,5)
(7) ¬Q4 - ЛР(2,5)
Применяя правило резолюции к дизъюнктам 6 и 7, получим пустой дизъюнкт
(8) ◻
Результативность лок-резолюции не зависит от того, как проиндексировать литеры в S.
Теорема. Пусть S множество дизъюнктов, в котором каждая литера индексирована целым числом. Если S противоречиво (неудовлетворимо), то имеется лок-вывод пустого дизъюнкта из S
Слайд 4
Линейная резолюция
Линейная резолюция довольно легко может быть реализована на
Линейная резолюция
Линейная резолюция довольно легко может быть реализована на

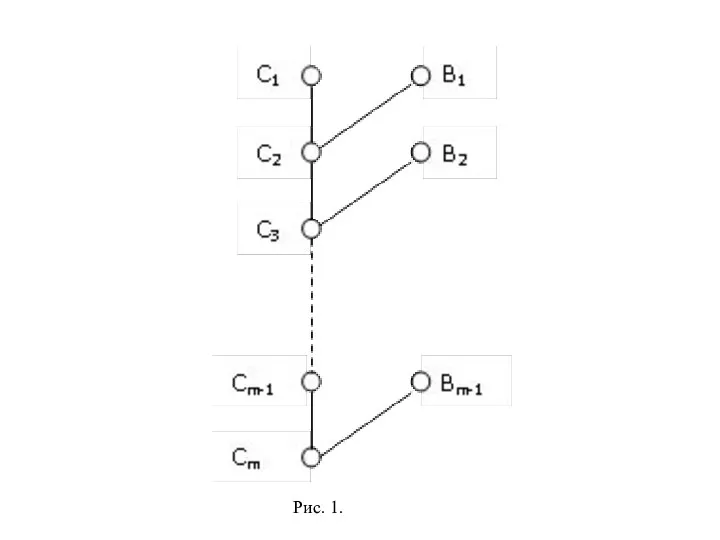
i = 1, 2, …, m-1, является резольвентой дизъюнкта Ci (называемого центральным дизъюнктом) и дизъюнкта Bi, (называемого боковым дизъюнктом), который удовлетворяет одному из двух условий:
Bi ∈ S (i = 1, 2, …, m-1);
2) Bi является некоторым дизъюнктом Cj, предшествующим в выводе дизъюнкту Ci, т.е. j < i (см. рис.1).
Слайд 5Рис. 1.
Рис. 1.
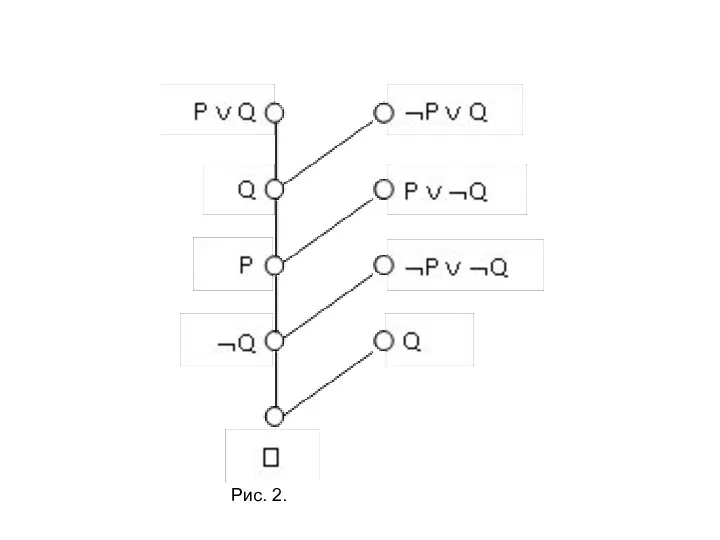
Слайд 6П р и м е р 1 . Пусть S = {P
П р и м е р 1 . Пусть S = {P

Теорема 1. Множество дизъюнктов невыполнимо тогда и только тогда, когда существует линейный вывод пустого дизъюнкта.
Слайд 7Рис. 2.
Рис. 2.
Слайд 82. OL-резолюция
Линейная резолюция может быть существенно усилена введением понятия упорядоченного дизъюнкта
2. OL-резолюция Линейная резолюция может быть существенно усилена введением понятия упорядоченного дизъюнкта

Отсюда упорядоченным дизъюнктом будем называть дизъюнкт с определенной последовательностью литер. Говорят, что литера L2 старше литры L1 в упорядоченном дизъюнкте тогда и только тогда, когда L2 следует за L1 в последовательности, определенной упорядоченным дизъюнктом. Отметим, что старшая (наибольшая) литера дизъюнкта является последней литерой дизъюнкта, а младшая литера – первой. Например, в упорядоченном дизъюнкте P(a) ∨ P(b) ∨ P(c)
P(c) является старшей литерой, а P(a) – младшей.
Слайд 9 Если две или больше литер (с одинаковыми знаками) упорядоченного дизъюнкта С
Если две или больше литер (с одинаковыми знаками) упорядоченного дизъюнкта С

Здесь имеются две идентичные литеры P(a). В соответствии с определением младшей литерой считается литера, расположенная левее.
Для получения упорядоченного фактора надо из Cσ удалить литеру, идентичную младшей литере. В нашем примере это последняя литера. Следовательно, упорядоченным фактором будет последовательность литер P(a) ∨ R(a).
Слайд 10
Отметим, что связывание понятия упорядоченных дизъюнктов с линейной резолюцией не нарушает
Отметим, что связывание понятия упорядоченных дизъюнктов с линейной резолюцией не нарушает

Однако оказывается, что эти литеры несут полезную информацию, которая может быть использована для усиления линейной резолюции.
Вернемся к примеру 1. Мы видим, что один из боковых дизъюнктов (дизъюнкт Q) не является входным дизъюнктом. Было бы полезно найти необходимое и достаточное условие, при котором центральный дизъюнкт, полученный ранее, становится боковым.
Дополнительное усиление рассмотренной стратегии было предложено Лавлендом, Ковальским и Кюнером. Ими установлены условия, при которых центральный дизъюнкт может позднее участвовать в роли бокового. Прежде всего, множество литер произвольным образом упорядочивается, т.е. становится известным, какую литеру в дизъюнкте поставить правее, а какую левее. Например, P>Q>R. Тогда упорядоченный дизъюнкт вида P∨Q∨R считается записанным верно, а дизъюнкт R∨P∨Q - нет. Кроме того, соответствующим образом записывается информация о резольвированных литерах. Вывод, использующий оба эти понятия, называется линейным упорядоченным выводом (OL-выводом (ordered linear deduction)).
Слайд 14 Таким образом, при получении редуцируемого упорядоченного дизъюнкта нет необходимости искать, с
Таким образом, при получении редуцируемого упорядоченного дизъюнкта нет необходимости искать, с

Будем называть это вычеркивание операцией редукции.
Операция редукции позволяет не запоминать в OL-выводе промежуточные дизъюнкты. Эта особенность OL-вывода делает его очень удобным при машинной реализации.
Операцию вычеркивания обрамленных литер, за которыми не следуют никакие другие литеры, будем называть операцией сокращения. Редуцируемый упорядоченный дизъюнкт образуется применением операций редукции и сокращения.
Упорядоченная бинарная резольвента упорядоченных дизъюнктов С1 и С2 получается конкатенацией последовательностей С1σ и С2σ, где σ есть НОУ для литер L1 и L2 = ¬L1 в С1 и С2 соответственно путем: 1) заключения в рамку L1σ; 2) вычеркивания L2σ; 3) вычеркивания любой необрамленной литеры, которая идентична младшей необрамленной литере последовательности; 4) применение операции сокращения.
Слайд 16 Теперь формально определим OL-вывод.
Пусть дано множество упорядоченных дизъюнктов S
Теперь формально определим OL-вывод.
Пусть дано множество упорядоченных дизъюнктов S

Слайд 17 Следующая теорема устанавливает полноту OL-резолюции (Лавленд, Ковальский, Кюнер).
Теорема 2. (о
Следующая теорема устанавливает полноту OL-резолюции (Лавленд, Ковальский, Кюнер).
Теорема 2. (о

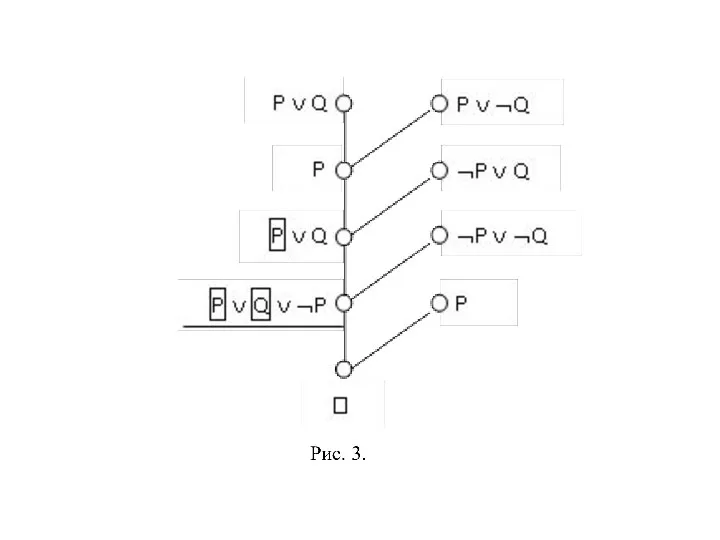
Слайд 19или в стандартной форме:
1. ¬C(x) ∨ O(x) ∨ P(f(x));
2. ¬C(x) ∨ O(x)
или в стандартной форме: 1. ¬C(x) ∨ O(x) ∨ P(f(x)); 2. ¬C(x) ∨ O(x)

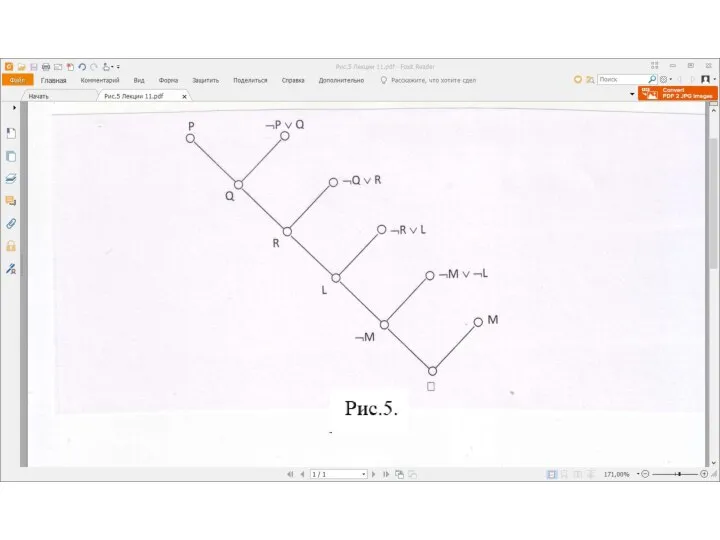
Дерево OL-вывода пустого дизъюнкта изображено на Рис. 4.
Слайд 20Рис. 4.
Рис. 4.
Слайд 21 Отметим, что OL-вывод успешно конкурирует со многими резолюционными методами вывода за
Отметим, что OL-вывод успешно конкурирует со многими резолюционными методами вывода за

Простота эта объясняется тем, что не нужно запоминать промежуточные дизъюнкты, а также тем, что здесь всегда определен один из резольвируемых дизъюнктов. OL-вывод – это по существу то же самое, что и метод элиминации моделей, как назвал его Лавленд, или специальный SL-вывод в смысле Ковальского и Кюнера, т.е. разновидность линейной резолюции с функцией выбора (selection function). Возвращаясь к примеру 1, мы обнаружили, что невозможно построить линейный вывод пустого дизъюнкта, если в качестве боковых дизъюнктов брать только дизъюнкты из исходного множества S (центральный дизъюнкт Q стал боковым). Назовем дизъюнкты из исходного множества S входными дизъюнктами.
Тогда резолюция, у которой хотя бы один из двух дизъюнктов при резольвировании является входным, называется входной резолюцией.
Слайд 22 Входная резолюция проста, эффективна, но в общем случае, к сожалению, как
Входная резолюция проста, эффективна, но в общем случае, к сожалению, как

¬P1 ∨ ¬ P2 ∨ … ∨ ¬ Pn ∨ Q
или в импликативной форме: P1 & P2 & … & Pn → Q.
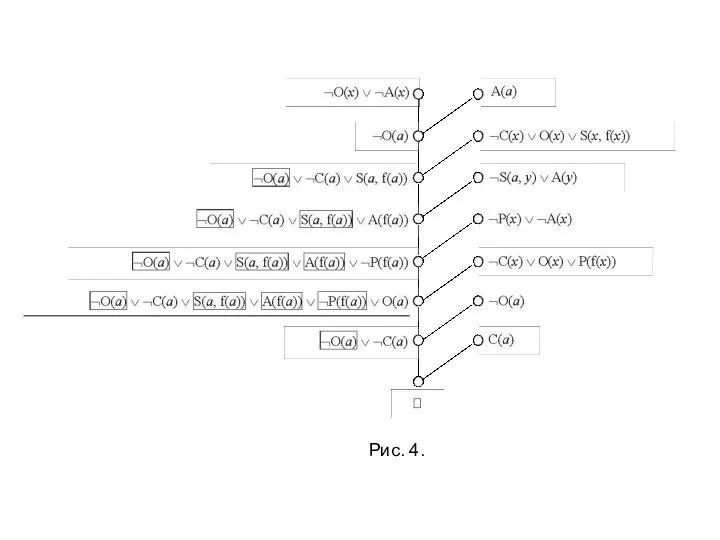
Возвращаясь к примеру, в котором детектив должен доказать, что, если горничная сказала правду, то дворецкий солгал, мы видели, что дерево вывода линейно и вывод пустого дизъюнкта был получен с помощью входной резолюции (см. след. слайд).
В этом примере все дизъюнкты из S были хорновскими в отличие от примера 1, где дизъюнкт P ∨ Q – нехорновский
Слайд 23П р и м е р (о детективе) . Горничная сказала, что
П р и м е р (о детективе) . Горничная сказала, что

Имеем следующее множество дизъюнктов: 1. ¬P ∨ Q, 2. ¬Q ∨ R, 3. ¬R ∨ L, 4. ¬M ∨ ¬L, и отрицание заключения ¬(¬P ∨ ¬M) 5. P, 6. M.
На рис. 5 приведено дерево вывода. Это дерево линейно и вывод пустого дизъюнкта был получен с помощью входной резолюции. В этом примере все дизъюнкты из S были хорновскими в отличие от примера 1, где дизъюнкт P∨Q – нехорновский.
Слайд 25 Входная резолюция и вывод в языке Пролог
В языке Пролог используется
Входная резолюция и вывод в языке Пролог В языке Пролог используется

Иногда систему вывода в языке Пролог называют SLD-резолюцией, т.е. SL-резолюцией для дефинициальных (definite) дизъюнктов, где под дефинициальным дизъюнктом понимают хорновский дизъюнкт. Логической программой является множество универсально квантифицированных выражений в логике предикатов вида
Q ← P1 & P2 & … & Pn. Здесь применяется обратная импликативная запись выражения.
Q и Pi (i = 1÷ n ) являются позитивными литерами, причем Q – заголовок дизъюнкта, а конъюнкция Pi – тело. Очевидно, что множество выражений является множеством хорновских дизъюнктов, которые могут быть трех видов:




 Диаграммы
Диаграммы Проекты сезона 2020-21
Проекты сезона 2020-21 Презентация на тему Решение экспериментальных задач
Презентация на тему Решение экспериментальных задач  Функция
Функция Функции. Их свойства
Функции. Их свойства Арифметическая прогрессия
Арифметическая прогрессия Окружность. Круг
Окружность. Круг Чётные и нечётные функции
Чётные и нечётные функции Действия с алгебраическими дробями
Действия с алгебраическими дробями Математическое ралли. Итоговое повторение 5 класс
Математическое ралли. Итоговое повторение 5 класс Линейная зависимость и линейная независимость системы векторов. Семинар 4
Линейная зависимость и линейная независимость системы векторов. Семинар 4 Ккомбинаторика. Перестановки. Размещения. Сочетания
Ккомбинаторика. Перестановки. Размещения. Сочетания Многогранники. Вершины, рёбра, грани многогранника. Развертка. Многогранные углы. Выпуклые многогранники. Теорема Эйлера
Многогранники. Вершины, рёбра, грани многогранника. Развертка. Многогранные углы. Выпуклые многогранники. Теорема Эйлера Задания со спичками
Задания со спичками Презентация на тему Свойства числовых неравенств
Презентация на тему Свойства числовых неравенств  Построение треугольника
Построение треугольника Основные сведения о матрицах. Операции над матрицами
Основные сведения о матрицах. Операции над матрицами Исследование функций
Исследование функций Точка и прямая на чертежах
Точка и прямая на чертежах Объемы и поверхности многогранников
Объемы и поверхности многогранников Линейная алгебра. Определители
Линейная алгебра. Определители Вычисление производных с помощью правил дифференцирования
Вычисление производных с помощью правил дифференцирования Конус
Конус Несобственные интегралы первого рода
Несобственные интегралы первого рода Шар и сфера
Шар и сфера ЕГЭ Профиль - Задание 6
ЕГЭ Профиль - Задание 6 Поверхности и тела. Проецирование геометрических фигур
Поверхности и тела. Проецирование геометрических фигур Построение графиков функций. Алгебра и начала анализа 11 класс
Построение графиков функций. Алгебра и начала анализа 11 класс