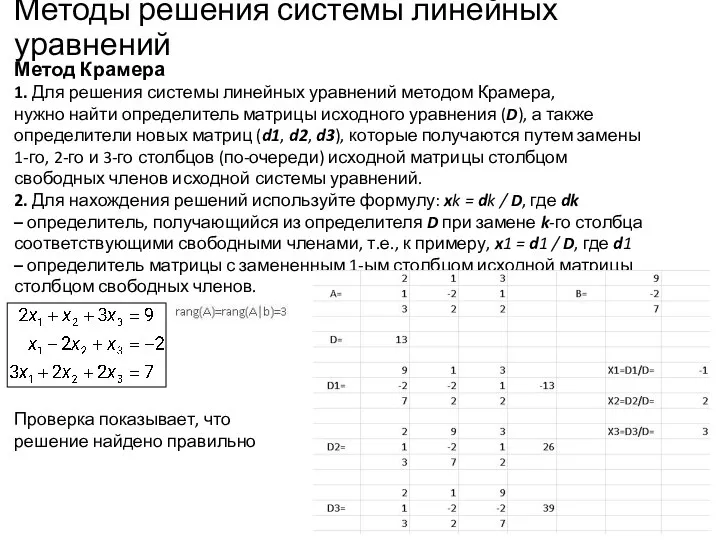
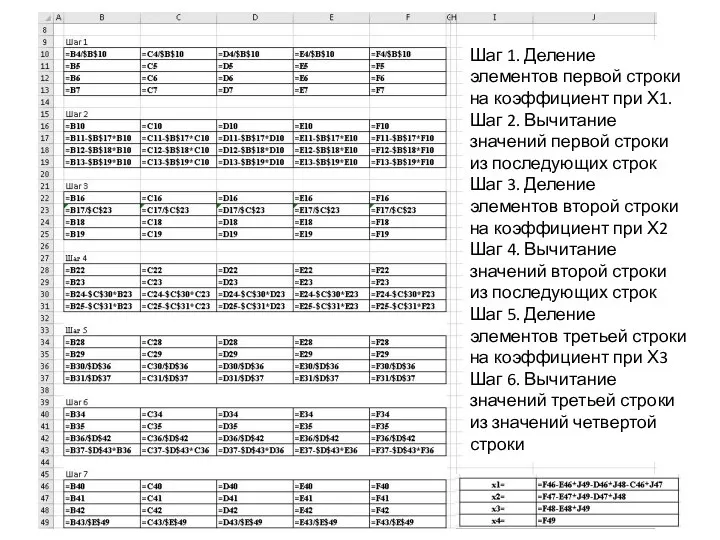
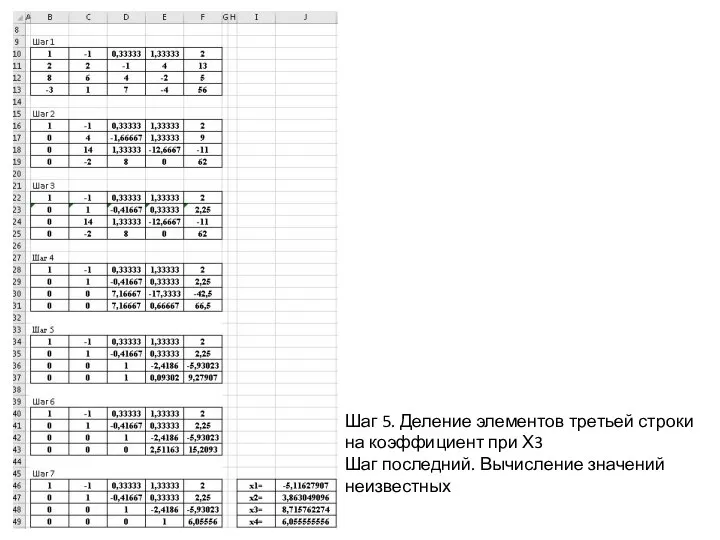
Крамера,
нужно найти определитель матрицы исходного уравнения (D), а также
определители новых матриц (d1, d2, d3), которые получаются путем замены
1-го, 2-го и 3-го столбцов (по-очереди) исходной матрицы столбцом
свободных членов исходной системы уравнений.
2. Для нахождения решений используйте формулу: xk = dk / D, где dk
– определитель, получающийся из определителя D при замене k-го столбца
соответствующими свободными членами, т.е., к примеру, x1 = d1 / D, где d1
– определитель матрицы с замененным 1-ым столбцом исходной матрицы
столбцом свободных членов.
Проверка показывает, что решение найдено правильно


 Вписанные углы
Вписанные углы Квадратичная функция и её график
Квадратичная функция и её график Вычисление площадей и объемов. Лекция 5
Вычисление площадей и объемов. Лекция 5 Восхождение на Пик Победы
Восхождение на Пик Победы Это полезно знать. Интересные факты из жизни самых больших чисел
Это полезно знать. Интересные факты из жизни самых больших чисел Відсоткі
Відсоткі Решение задач. Повторение пройденного
Решение задач. Повторение пройденного Умножение многозначных чисел на однозначное и двузначное число. Урок – путешествие (закрепление) по математике, 4 класс Состави
Умножение многозначных чисел на однозначное и двузначное число. Урок – путешествие (закрепление) по математике, 4 класс Состави Презентация на тему Учим состав числа от 5 до 10
Презентация на тему Учим состав числа от 5 до 10  Решение задач на проценты. Урок - сказка
Решение задач на проценты. Урок - сказка Обыкновенные дроби
Обыкновенные дроби Презентация на тему НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
Презентация на тему НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ  Презентация на тему Двугранный угол (10 класс)
Презентация на тему Двугранный угол (10 класс)  Перетворення подібності. Гомотерапія
Перетворення подібності. Гомотерапія Деление. Неправильные дроби
Деление. Неправильные дроби Числовыe последовательности
Числовыe последовательности Правильная пирамида
Правильная пирамида Объёмные и плоские предметы. 1 класс
Объёмные и плоские предметы. 1 класс Дроби. 5 класс
Дроби. 5 класс Геометрический конструктор GeoGebra
Геометрический конструктор GeoGebra Неопределённый интеграл
Неопределённый интеграл Вычислительная математика. Практика №2
Вычислительная математика. Практика №2 Решение уравнений сводящихся к линейным
Решение уравнений сводящихся к линейным Скалярное произведение векторов
Скалярное произведение векторов Тригонометрия. Контрольная работа
Тригонометрия. Контрольная работа Интерактивный тренажёр В стране Математики. 1 класс
Интерактивный тренажёр В стране Математики. 1 класс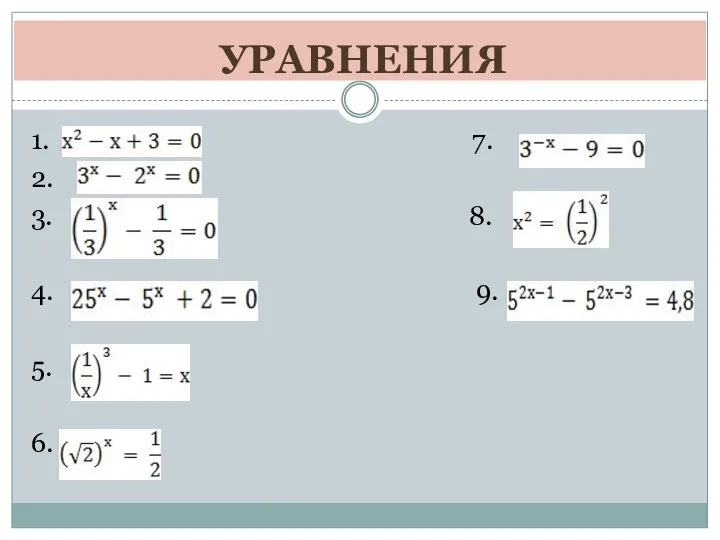 Решение показателей уравнений
Решение показателей уравнений Решение задач с помощью систем уравнений
Решение задач с помощью систем уравнений