Координаты вектора

Цель:
Ввести понятие координат вектора и рассмотреть правила действий над векторами с заданными координатами.

Дайте определение вектора.
Какой вектор называется нулевым?
Длина вектора.
Чему равна длина нулевого вектора?
Какие векторы называются коллинеарными?
Дайте определение равных векторов.
Что значит «Вектор отложен от данной точки?
Сколько векторов равных данному можно отложить от данной точки?
Без теории нет практики

В чем заключается правило треугольника сложения двух векторов?
В чем заключается правило параллелограмма сложения двух векторов?
Какой вектор называется разностью двух векторов?
Какой вектор называется противоположным данному?
Какой вектор называется произведением данного вектора на данное число ?
Сформулируйте основные свойства умножения вектора на число.
Без теории нет практики

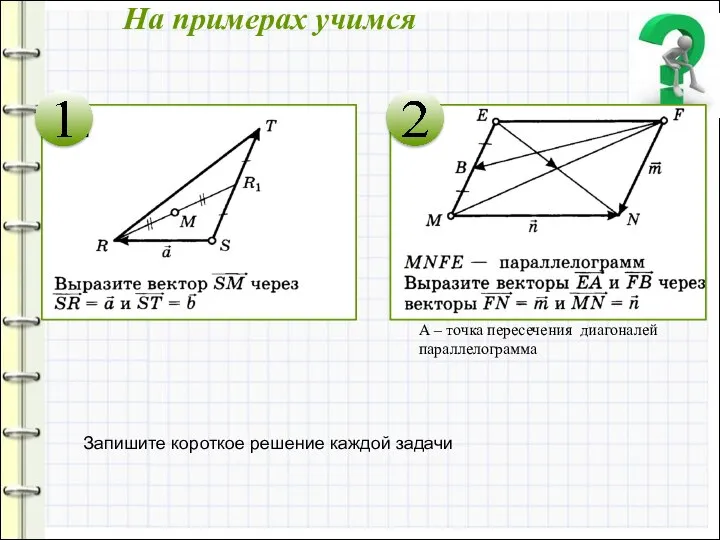
На примерах учимся
Запишите короткое решение каждой задачи
А – точка пересечения диагоналей параллелограмма

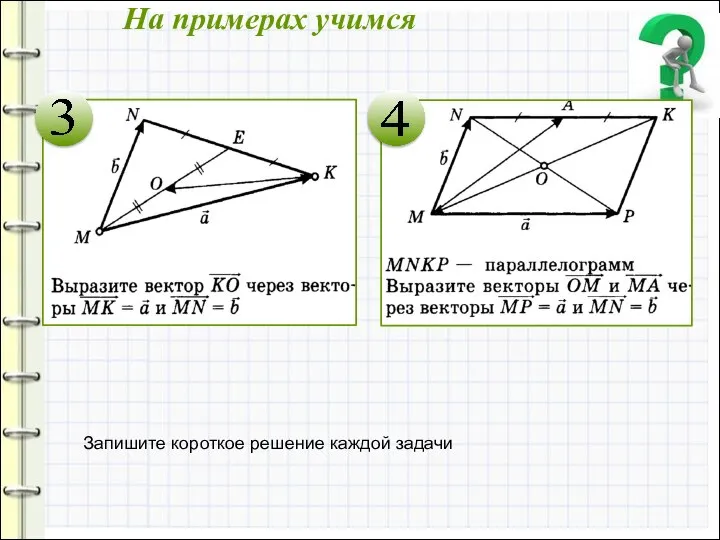
На примерах учимся
Запишите короткое решение каждой задачи

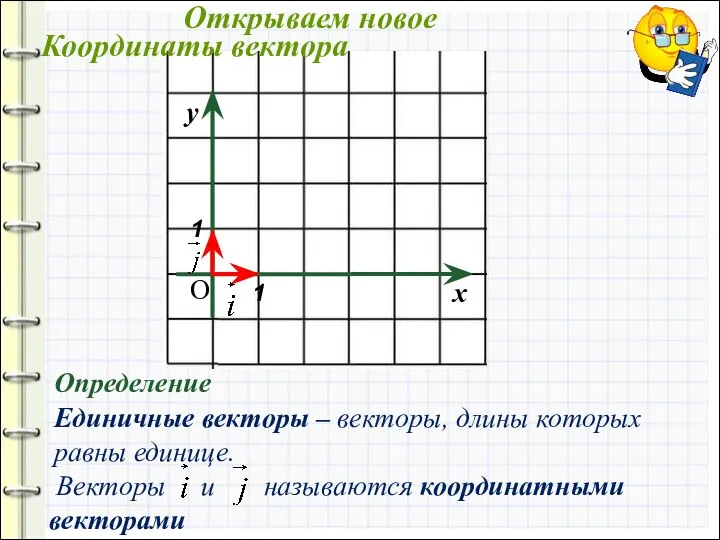
О
Координаты вектора
Определение
Единичные векторы – векторы, длины которых равны единице.
Открываем новое

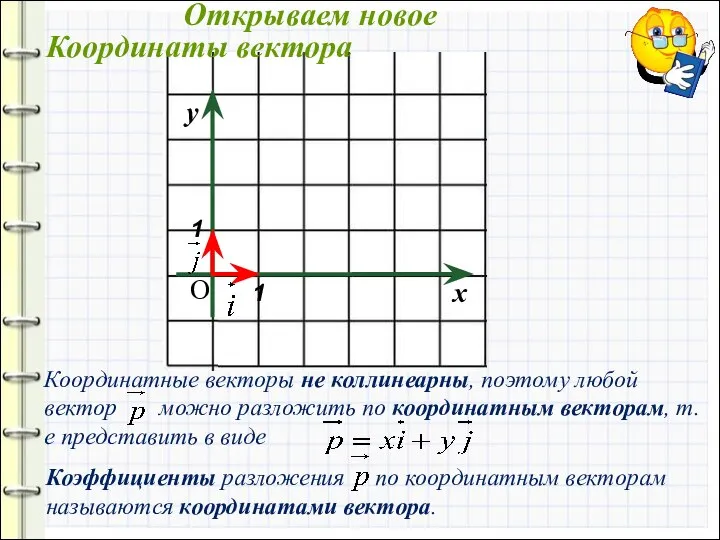
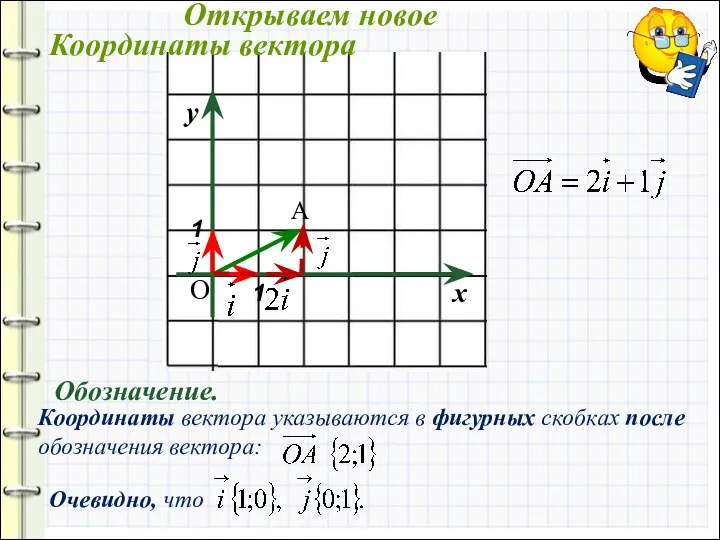
О
Координаты вектора
Открываем новое

О
Обозначение.
Координаты вектора
Координаты вектора указываются в фигурных скобках после обозначения вектора:
Очевидно, что
Открываем новое

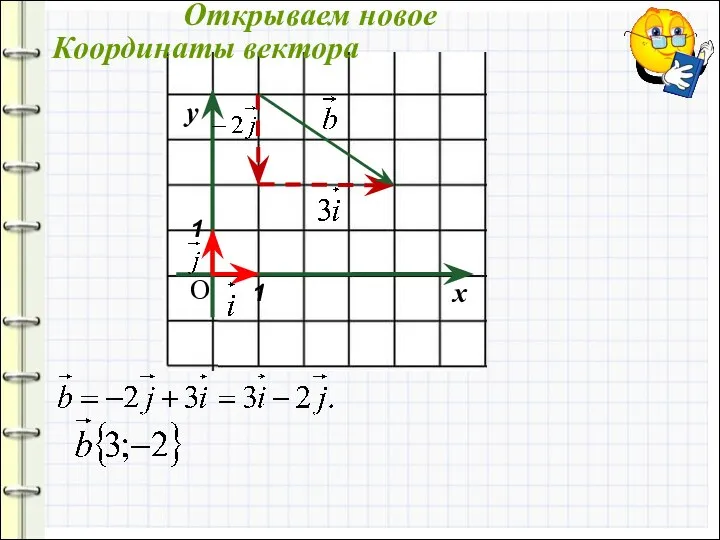
О
Координаты вектора
Открываем новое

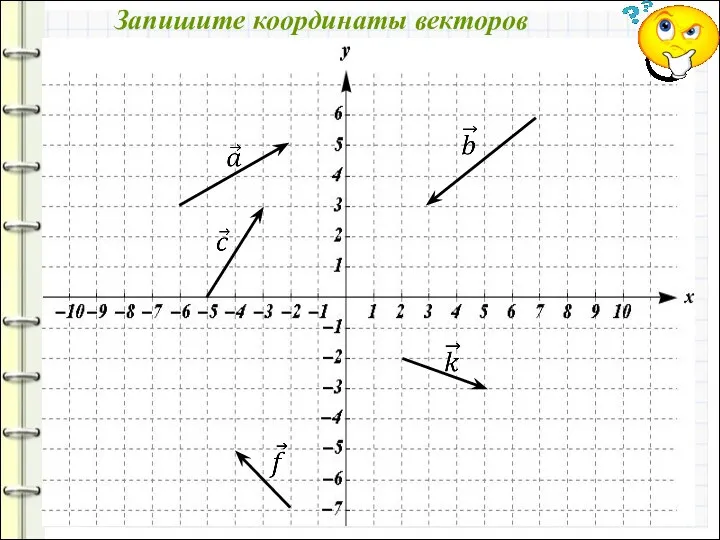
Запишите координаты векторов

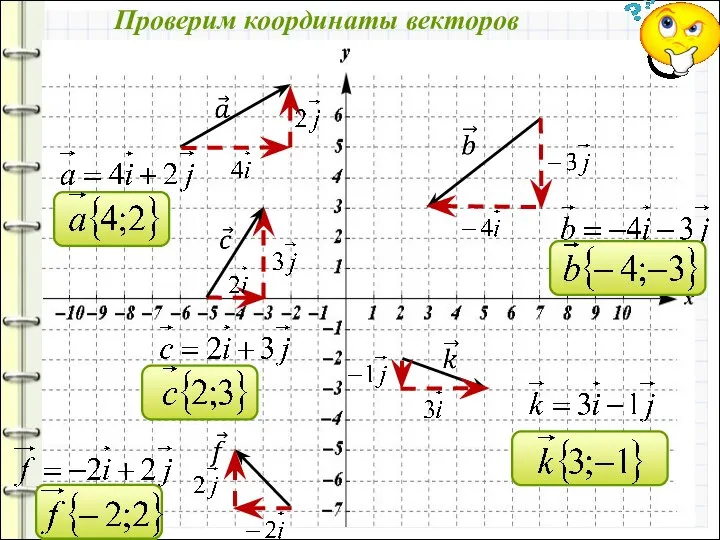
Проверим координаты векторов

Назовите координаты векторов

Разложите вектор по координатным векторам

Пример №921 (а, б)
Свойства координатных векторов

1. Каждая координата суммы двух векторов или более векторов равна сумме соответствующих координат этих векторов.
Координаты вектора
Пример №922(а, б)

Координаты вектора
2. Каждая координата разности двух векторов равна разности соответствующих координат этих векторов.
№923 (а, б)

3. Каждая координата произведения вектора на число равна произведению соответствующей координаты на это число.
Координаты вектора
№924 (а, б)

Координаты вектора

На примерах учимся

Ответить на вопросы:
Дайте определение координатных векторов?
Cформулируйте утверждение о разложении вектора по координатным векторам.
Дайте определение координат вектора?
Как связаны между собой координаты равных векторов?
Сформулируйте правила нахождения координат суммы и разности векторов.
Сформулируйте правило нахождения координат произведения вектора на число по заданным координатам векторов.

Математический диктант