Системы принятия решений. Алгоритмы оптимизации

Характеристические алгоритмы оптимизации
1. Задать множество
конечного числа точек области , полагая, что
, все координаты предшествующих испытаний
множество упорядочено (нижним индексом) по возрастанию координаты, т.е.
и сопоставить точкам множества значения

Характеристические алгоритмы оптимизации
2. Каждому интервалу , , поставить в соответствие число , называемое характеристикой этого интервала.
3. Определить интервал , которому соответствует максимальная характеристика , т.е.
4. Провести очередное испытание в точке
и вычислить значение

Двусторонняя сходимость.
(2.3)
тогда для характеристики этого интервала выполняется строгое неравенство
где в (2.2), (2.4), (2.5) величины μ, c, и ν некоторые константы, причем

Следствие. В вычислительную схему алгоритма, удовлетворяющего условиям Теоремы 2.1, может быть введено условие остановки вида
(2.7)
Двусторонняя сходимость.

Двусторонняя сходимость (перебор)
iii) для точек новых испытаний

Двусторонняя сходимость (метод Пиявского)
Условие Липшица

Двусторонняя сходимость (метод Пиявского)
ii) если
тогда
Возьмем
Вследствие условия Липшица

Двусторонняя сходимость (метод Пиявского)
iii) для точек новых испытаний

Двусторонняя сходимость (метод Стронгина)
Условие Липшица

Двусторонняя сходимость (метод Стронгина)
ii) если
тогда
Возьмем
Случай 1.
Случай 2.

Двусторонняя сходимость (метод Стронгина)
iii) для точек новых испытаний
- параметр метода

Двусторонняя сходимость (метод Кушнера)
Потребуем непрерывность целевой функции

Двусторонняя сходимость (метод Кушнера)
Но любой интервал, в который испытания больше не попадают, имеет положительную длину, что доказывает требуемое неравенство.

Двусторонняя сходимость (метод Кушнера)
iii) для точек новых испытаний
Рассмотрим разности
где

Двусторонняя сходимость (метод Кушнера)
Кроме того, функция возрастает по w для любого положительного α , т.к.
Последнее неравенство означает, что
следовательно,
Таким образом, в качестве константы ν в (2.6) можно взять величину
которая, очевидно, положительна и меньше единицы.

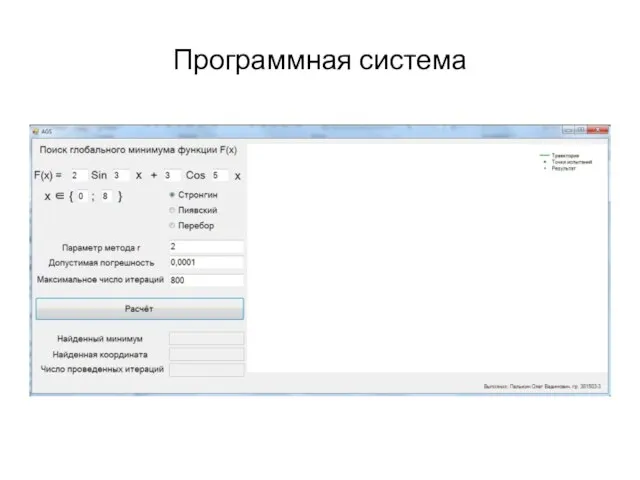
Программная система