Содержание
- 2. Системы линейных уравнений. Основные понятия.
- 3. «Мне приходится делить время между политикой и уравнениями. Однако уравнение, по-моему,гораздо важнее. Политика существует только для
- 4. Дорогу осилит идущий, а математику – мыслящий.
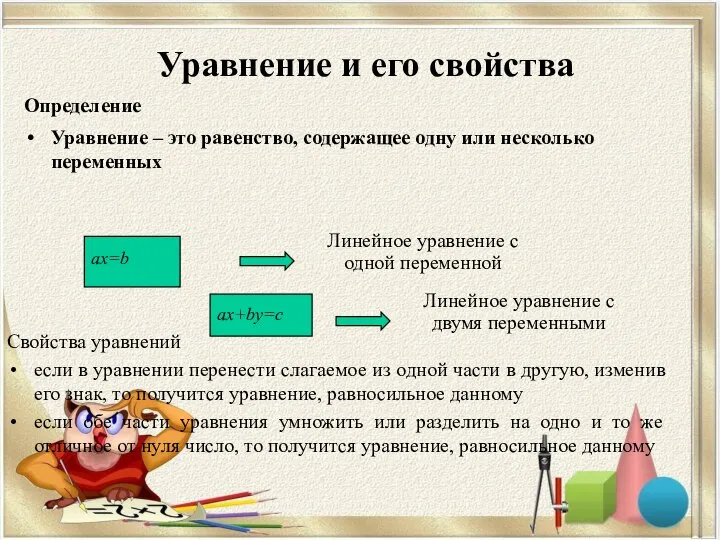
- 5. Определение Уравнение – это равенство, содержащее одну или несколько переменных Линейное уравнение с одной переменной Линейное
- 6. ЗНАКОМТЕСЬ.......... Системой уравнений называется некоторое количество уравнений, объединенных фигурной скобкой. Фигурная скобка означает, что все уравнения
- 7. Система линейных уравнений с двумя неизвестными Сумма двух чисел равна 12, а разность равна 2. Найдите
- 8. Пара значений x = 7 и y = 5 являются решением данной системы. Решением системы уравнений
- 9. Решить систему уравнений - значит найти все её решения, либо доказать, что их нет
- 10. Работа в классе
- 11. СПОСОБЫ РЕШЕНИЙ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ Системы линейных уравнений Графический способ Способ подстановки Способ сложения
- 12. Выразим переменную у через х в каждом уравнении Построим графики всех получившихся линейных функций Найдем координаты
- 13. Выразить у через х в каждом уравнении Построить в одной системе координат график каждого уравнения Определить
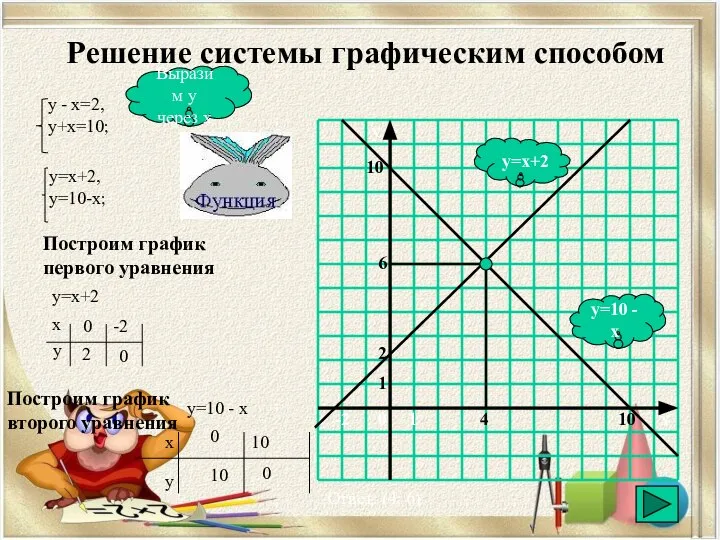
- 14. Решение системы графическим способом y=10 - x y=x+2 Выразим у через х Построим график первого уравнения
- 15. 2х + у = -3, 3х + у = 1 y = -2x-3, у = -3x+1
- 16. Способ сравнения (алгоритм) Выразить у через х (или х через у) в каждом уравнении Приравнять выражения,
- 17. Решение системы способом подстановки Приравняем выражения для у 7х - 1=2х+4, 7х - 2х=4+1, 5х=5, х=1.
- 18. Закрепление: №5.3(а) №5.7(а) №5.12(а)
- 20. Скачать презентацию















 Дифференцирование показательной и логарифмической функций
Дифференцирование показательной и логарифмической функций В стране геометрических фигур (форма, размер, цвет)
В стране геометрических фигур (форма, размер, цвет) Арифметический квадратный корень
Арифметический квадратный корень Натуральные числа и дроби. Урок 1
Натуральные числа и дроби. Урок 1 Круговая окружность
Круговая окружность Среднее арифметическое
Среднее арифметическое Презентация на тему Перевод целых чисел в 2, 8, 16-ую системы счисления
Презентация на тему Перевод целых чисел в 2, 8, 16-ую системы счисления 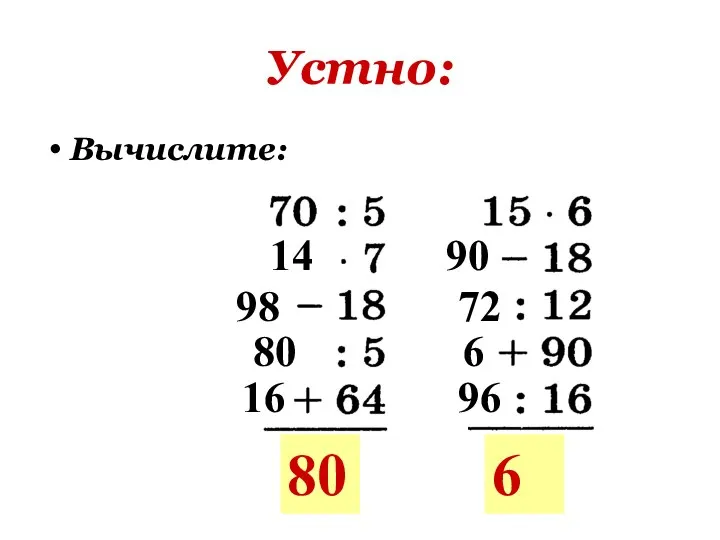 Устно. Вычисления
Устно. Вычисления Презентация на тему Умножение и деление десятичной дроби на 10, 100, 1000 и т.д.
Презентация на тему Умножение и деление десятичной дроби на 10, 100, 1000 и т.д.  lobachevsky
lobachevsky Сложение и вычитание положительных десятичных дробей
Сложение и вычитание положительных десятичных дробей Золотое сечение
Золотое сечение Арифметическая прогрессия
Арифметическая прогрессия Взаимно обратные числа
Взаимно обратные числа Теорема Пифагора
Теорема Пифагора Статистические графики
Статистические графики ложение комплексных чисел. Вычитание комплексных чисел
ложение комплексных чисел. Вычитание комплексных чисел Булева алгебра
Булева алгебра Зимующие птицы. Дети 5 лет
Зимующие птицы. Дети 5 лет Числа от 1 до 100. Умножение и деление. Закрепление
Числа от 1 до 100. Умножение и деление. Закрепление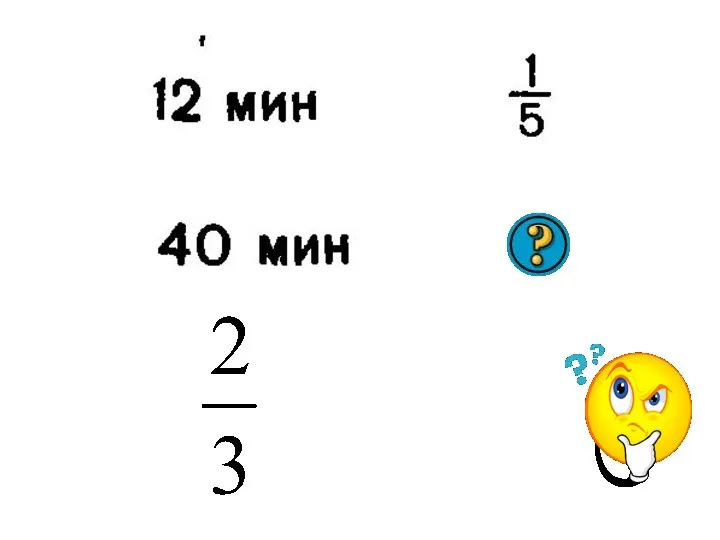 Задания по математике (5 класс, часть 7)
Задания по математике (5 класс, часть 7) Геометрический смысл производной
Геометрический смысл производной Векторы на плоскости
Векторы на плоскости Интерактивный тренажёр. Сложение и вычитание в пределах первого десятка. 3 уровень
Интерактивный тренажёр. Сложение и вычитание в пределах первого десятка. 3 уровень Синус, косинус и тангенс угла
Синус, косинус и тангенс угла Курс по математике ОГЭ 2021
Курс по математике ОГЭ 2021 Проценты (1)
Проценты (1) Деление обыкновенных дробей
Деление обыкновенных дробей