Случайные события и величины

ОБРАЗОВАТЕЛЬНЫЙ ПОРТАЛ ИГУ
Запись на курс Теория вероятностей и математическая статистика

ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
1. Элементы комбинаторики
2. Случайные события
3. Случайные величины
Одномерные с.в.
Многомерные с.в.
4. Предельные теоремы т.в.
5. Элементы математической статистики
25 задач +защита решения
Контрольная работа
Семестровое задание
Домашняя исследовательская работа
Домашняя контрольная работа

СЛУЧАЙНЫЕ СОБЫТИЯ И ВЕЛИЧИНЫ
Защита решения любых 5 задач из
25 задач
Контрольная работа – 10 б.
Семестровое задание – 30 б.
Домашняя контрольная работа – 10 б.
10
50
Случайные события
Случайные величины

ЗАЧЕТ
БРС
60 + 30 + 10 =100
10+50
10 – презентация
20 – домашняя иссл. работа
Олимпиада по т.в

ДОМАШНЯЯ ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА
Центральная предельная теорема и ее следствия.
Проверить выполнение ЦПТ.
4.1. Сгенерировать результаты наблюдений случайных величин
Хi ~ R (0,1), i=1, 2, ….n. !!!!
4.2. Образовать суммы: S2=X1+X2, S3= X1+X2 +X3 , …. Sn= X1+X2+…Xn.
4.3. Построить гистограммы для X1, S2, S3, …. Sn.

http://eek.diary.ru/p47642323.htm
http://www.matburo.ru/st_subject.php?p=tv
Теория вероятностей: учебники, лекции, сайты
On-line ресурсы по теории вероятностей

Т.Л. Агекян Теория вероятностей для астрономов и физиков. М., Главная редакция физико-математической литературы издательства «Наука», 1974. - 264 стр.
В книге изложены элементы теории вероятностей в том виде, в каком они должны в первую очередь находить применение в астрономии и физике.
Предназначение книги требовало удобства использования излагаемого материала для исследований в области астрономии и физики. Приведено значительное число примеров, главным образом астрономических и физических. Книга может быть использована в качестве учебного пособия при чтении курса теории вероятностей для студентов университетов, специализирующихся по астрономии и физике.

Пытьев Ю. П. Шишмарев И. А. Курс теории вероятностей и математической статистики для физиков: Учеб. пособие. — М.: Изд-во Моск. ун-та, 1983. — 256 с.
В основу книги положен полугодовой курс лекций, читаемый авторами на физическом факультете. Большое место уделено теории случайных процессов: марковских и стационарных. Изложение математически строгое, хотя и не основанное на использовании интеграла Лебега. Часть курса, посвященная математической статистике, содержит разделы, ориентированные на приложения к задачам автоматизации планировании, анализа и интерпретации физических экспериментов. Включены элементы теории статистической проверки гипотез, используемые в задаче интерпретации экспериментальных данных.

Гнеденко Б.В. Курс теории вероятностей: Учебник. - Изд. 8-е, испр. и доп. — М.: Едиториал УРСС, 2005. — 448 с. (Классический университетский учебник.).
Дается систематическое изложение основ теории вероятностей, проиллюстрированное большим числом подробно рассмотренных примеров, в том числе и прикладного содержания. Серьезное внимание уделено рассмотрению вопросов методологического характера.

Гмурман В. Е. Теория вероятностей и математическая статистика - М., Высш.шк., 2003.- 479 с.
Учебное пособие содержит в основном весь материал программы по теории вероятностей и математической статистике. Большое внимание уделено статистическим методам обработки экспериментальных данных. В конце каждой главы помещены задачи с ответами. Предназначается для студентов вузов и лиц, использующих вероятностные и статистические методы при решении практических задач.
Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статистике. - М., Высш.шк., 2004.- 404 с.
В руководстве к решению задач приведены необходимые теоретические сведения и формулы, даны решения типовых задач, помещены задачи для самостоятельного решения, сопровождающиеся ответами и указаниями. Большое внимание уделено методам статистической обработки экспериментальных данных.

Вуколов Э. Л. Основы статистического анализа. Практикум по статистическим методам и исследованию операции с использованием пакетов STATISTICA и EXCEL: учебное пособие. — 2-е изд., исправ. и доп.. — М.: ФОРУМ. 2008. — 464 с. — (Высшее образование).
Книга является учебно-методическим пособием по теории вероятностей, статистическим методам и исследованию операций. Приведены необходимые теоретические сведения и подробно рассматривается решение задач прикладной статистики с использованием пакета STATISTICA. Излагаются основы симплекс-метода и рассматривается решение задач исследования операций средствами пакета EXCEL. Приводятся варианты заданий и методические разработки по основным разделам статистики и исследования операций.

Свешников А.А. Сборник задач по теории вероятностей, математической статистике и теории случайных величин - Изд.: Лань, 2008, 448 стр. .
Дается систематическое изложение основ теории вероятностей, проиллюстрированное большим числом подробно рассмотренных примеров, в том числе и прикладного содержания. Серьезное внимание уделено рассмотрению вопросов методологического характера.

Кремер Н.Ш. Теория вероятностей и математическая статистика: Учебник для вузов. — 2-е изд., перераб. и доп.— М.: ЮНИТИ-ДАНА, 2004. - 573 с.
Основной принцип, которым руководствовался автор при подготовке курса теории вероятностей и математической статистики для экономистов, — повышение уровня фундаментальной математической подготовки студентов с усилением ее прикладной экономической направленности. При этом это не только учебник, но и краткое руководство к решению задач. Приводятся примеры использования вероятностных и математико-статистических методов в задачах массового обслуживания и моделях финансового рынка. Задачи для самостоятельной работы рассматриваются в конце каждой главы в рубрике «Упражнения». Необходимые для решения задач математико-статистические таблицы даются в приложении.

В. А. Ватутин и др. Теория вероятностей и математическая статистика в задачах: Учеб. пособие для вузов/В. А. Ватутин, Г. И. Ивченко, Ю- И. Медведев и др. — 2-е изд., испр. — М.: Дрофа, 2003. — 328 с: ил.
Для каждой модели приведены краткие теоретические сведения, примеры решения задач и задачи дли самостоятельного решения. Среди прикладных задач имеются задачи по теории страхования и экономике.
Книга может быть использована для нескольких целей:
1. как справочник, позволяющий быстро найти образец решения того или иного класса задач;
2. для самостоятельного изучения теории вероятностей и математической статистики;
3. как основа ознакомительного курса теории вероятностей.

ПЛАНИРОВАНИЕ
ЛЕКЦИИ
5.09 – Случайные события
19.09
3.10
17.10
31.10
14.11 – Многомерные случайные величины
28.11 – Предельные теоремы т.в.
12.12 – Математическая статистика
26. 12 – зачет
ПРАКТИКА
5 (12).09 - комбинаторика
19 (26).09 – случайные события
3 (10).10 – случайные величины
17 (24).10 – случайные величины
31(7).10 – контрольная работа
14 (21).11 – защита семестрового задания
28 (5).11 – сдать д.к.р.
12 (19).12 – ЗАЧЕТ
26.12 – ЗАЧЕТ
Одномерные случайные
величины
1
2
3
4
5
6
7
8

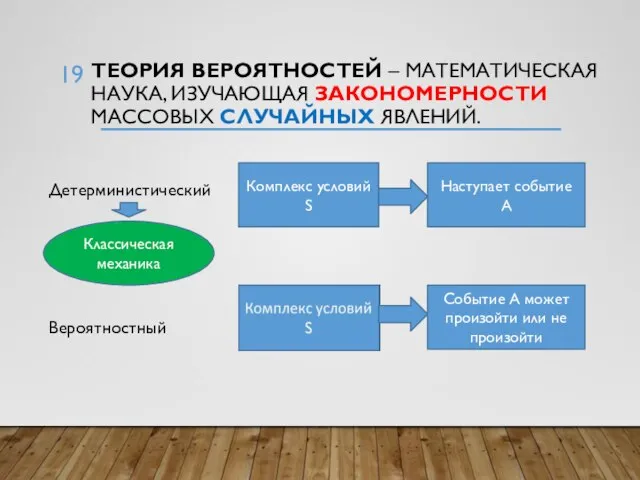
ТЕОРИЯ ВЕРОЯТНОСТЕЙ – МАТЕМАТИЧЕСКАЯ НАУКА, ИЗУЧАЮЩАЯ ЗАКОНОМЕРНОСТИ МАССОВЫХ СЛУЧАЙНЫХ ЯВЛЕНИЙ.
Детерминистический
Вероятностный
Комплекс условий S
Наступает событие А
Событие А может произойти или не произойти
Классическая механика