- Главная
- Математика
- Умножение вектора на число

Содержание
Слайд 3Умножение вектора на число
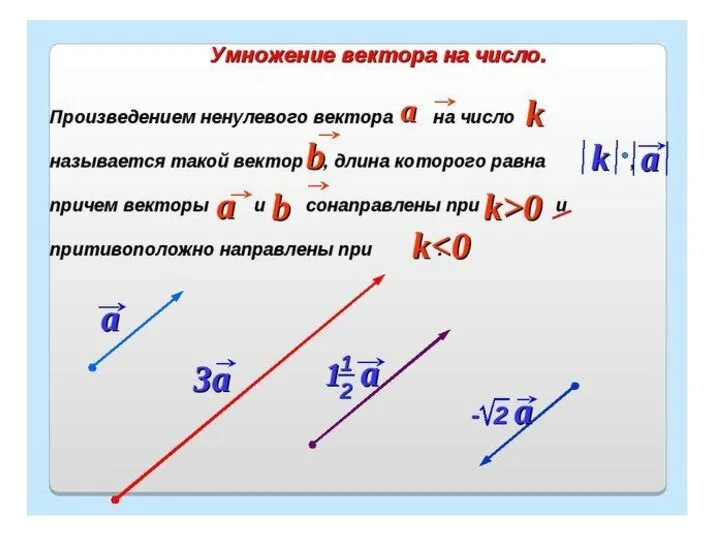
Произведением ненулевого вектора а на число k называется такой
Умножение вектора на число
Произведением ненулевого вектора а на число k называется такой

вектор b, длина которого
равна |k|*|а|, причем векторы а и b сонаправлены при k > O и противоположно направлены при k<0.
Произведением нулевого вектора на любое число считается нулевой вектор.
Произведение вектора а на число k обозначается так: ka.
Для любого числа k и любого вектора а векторы а и ka коллинеарны.
Произведение любого вектора на число нуль есть нулевой вектор.
равна |k|*|а|, причем векторы а и b сонаправлены при k > O и противоположно направлены при k<0.
Произведением нулевого вектора на любое число считается нулевой вектор.
Произведение вектора а на число k обозначается так: ka.
Для любого числа k и любого вектора а векторы а и ka коллинеарны.
Произведение любого вектора на число нуль есть нулевой вектор.
Слайд 4Свойства умножения вектора на число
Для любых векторов а, b и любых
Свойства умножения вектора на число
Для любых векторов а, b и любых

чисел k, f справедливы равенства:
(kf)a=k(fa) ( сочетательный закон);
k(a + b)= ka + kb (первый распределительный закон);
(k + f) a =ka + fa (второй распределительный закон).
(kf)a=k(fa) ( сочетательный закон);
k(a + b)= ka + kb (первый распределительный закон);
(k + f) a =ka + fa (второй распределительный закон).
 Виды треугольников. 5 класс
Виды треугольников. 5 класс Устный счет. Умножение положительных и отрицательных чисел
Устный счет. Умножение положительных и отрицательных чисел Разминка. Линейная функция
Разминка. Линейная функция Решение систем неравенств первой степени с одним неизвестным
Решение систем неравенств первой степени с одним неизвестным Математическая викторина
Математическая викторина Определение общего числа единиц, десятков, сотен в числе
Определение общего числа единиц, десятков, сотен в числе Методы решения задач на смеси и сплавы
Методы решения задач на смеси и сплавы Вычитание натуральных чисел
Вычитание натуральных чисел Отношения эквивалентности. Частичный порядок на множестве. Линейный порядок на множестве
Отношения эквивалентности. Частичный порядок на множестве. Линейный порядок на множестве Приёмы устных вычислений
Приёмы устных вычислений Аксиомы стереометрии. Следствия из аксиом
Аксиомы стереометрии. Следствия из аксиом Числа. Комплексные числа
Числа. Комплексные числа Угол между векторами
Угол между векторами Презентация на тему ВЕСЁЛЫЙ СЧЁТ
Презентация на тему ВЕСЁЛЫЙ СЧЁТ  Презентация на тему КВАДРАТНЫЙ ТРЕХЧЛЕН
Презентация на тему КВАДРАТНЫЙ ТРЕХЧЛЕН  Параллельность прямых. Домашнее задание
Параллельность прямых. Домашнее задание Основное свойство дроби
Основное свойство дроби Обратное Z - преобразование
Обратное Z - преобразование Презентация на тему Комбинаторика
Презентация на тему Комбинаторика  Консультация ДУ
Консультация ДУ Математическая интеллектуальная игра для всей семьи
Математическая интеллектуальная игра для всей семьи Презентация на тему Медианы, биссектрисы и высоты треугольника (7 класс)
Презентация на тему Медианы, биссектрисы и высоты треугольника (7 класс)  Сумма углов треугольника
Сумма углов треугольника Вписанный угол
Вписанный угол Кратные числа
Кратные числа Абсолютная величина
Абсолютная величина Пропорциональное деление
Пропорциональное деление Функции
Функции