Содержание
- 2. Случайные величины Случайная величина - это переменная, которая в результате испытания принимает одно из своих возможных
- 3. Закон распределения - соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими вероятностями, с которыми
- 4. - математическое ожидание произведения постоянной величины С и случайной ветчины X равно произведению этой константы на
- 5. - математическое ожидание алгебраической суммы случайной величины X и постоянной величины С равно алгебраической сумме этой
- 6. - дисперсия произведения постоянной величины С и случайной величины X равна произведению квадрата этой константы на
- 7. Дискретная случайная величина Дискретная случайная величина - случайная величина, которая принимает конечное или бесконечное, но счетное
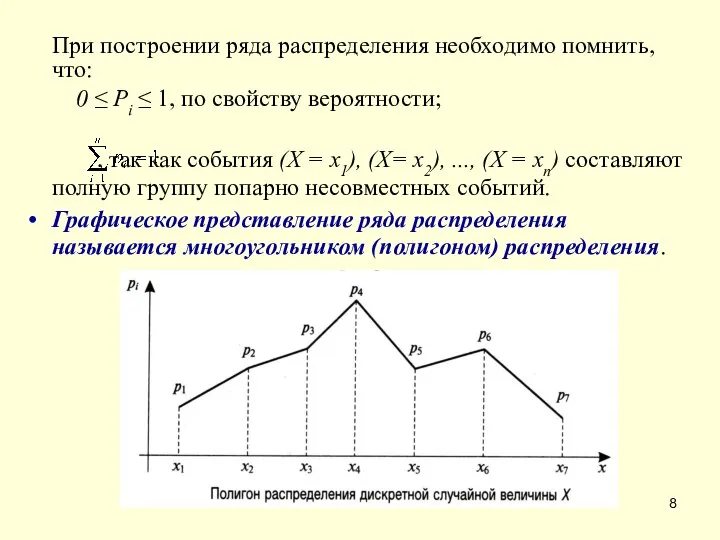
- 8. При построении ряда распределения необходимо помнить, что: 0 ≤ Pi ≤ 1, по свойству вероятности; ,
- 9. Функция распределения дискретной случайной величины Функция распределения (интегральная функция) F(x) определяет для каждого возможного значения х
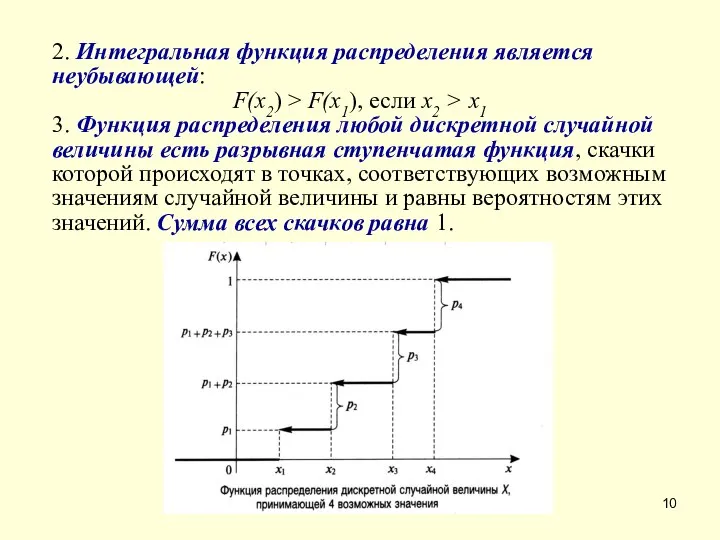
- 10. 2. Интегральная функция распределения является неубывающей: F(x2) > F(x1), если х2 > х1 3. Функция распределения
- 11. Основные числовые характеристики дискретной случайной величины 1. Математическое ожидание дискретной случайной величины определяется по формуле: 2.
- 12. Пример. Вероятность всхожести семян некоторого растения равна 0,8. Составить закон распределения числа взошедших семян из трех
- 13. Вероятность того, что взойдет ровно одно семя: p2 = 3pq2 = 3·0,8·0,22 = 0,096. Вероятность того,
- 14. Основные законы распределения дискретных случайных величин Биномиальный закон распределения - закон распределения дискретной случайной величины X,
- 15. Математическое ожидание и дисперсия дискретной случайной величины X, имеющей биномиальный закон распределения, равны: М(Х) = п
- 16. Закон распределения Пуассона - закон распределения дискретной случайной величины X, представляющей собой число т наступлений события
- 17. Дискретная случайная величина имеет закон распределения Пуассона с параметром X, если она принимает целочисленные неотрицательные значения
- 18. Пример. В приемное время врача посещает в среднем 7 человек в час. Составить закон распределения числа
- 19. Случайная величина X может принимать числовые значения: х0 = 0, х1 = 1, х2 = 2,
- 20. Геометрическое распределение Если дискретная случайная величина может принимать только значения целых натуральных чисел с вероятностями P(X
- 21. Пример. Вероятность поражения мишени стрелком равна р = 0,7. Случайная величина Х – это число выстрелов
- 23. Скачать презентацию


















 Робот Гоша ведёт занятие по ФЭМП
Робот Гоша ведёт занятие по ФЭМП Вычисление и сравнение логарифмов
Вычисление и сравнение логарифмов Перпендикуляр и наклонная. Угол между прямой и плоскостью
Перпендикуляр и наклонная. Угол между прямой и плоскостью Форма прямоугольника
Форма прямоугольника Решение систем с неизвестными множествами
Решение систем с неизвестными множествами Презентация на тему Небесная геометрия - снежинки
Презентация на тему Небесная геометрия - снежинки  Угол между прямой и плоскостью
Угол между прямой и плоскостью Прямоугольник. Ось симметрии
Прямоугольник. Ось симметрии Интересное о математике
Интересное о математике Треугольник
Треугольник Реляционная алгебра
Реляционная алгебра Десятичная запись дробных чисел
Десятичная запись дробных чисел Составные задачами, новые способы решения
Составные задачами, новые способы решения Декартова система координат на плоскости. Математика, 6 класс
Декартова система координат на плоскости. Математика, 6 класс Координатная плоскость (урок 2)
Координатная плоскость (урок 2) Функция
Функция ЧМ МНП. Занятие 1 (магистры ФН)
ЧМ МНП. Занятие 1 (магистры ФН) Построение графика квадратичной функции
Построение графика квадратичной функции Теория вероятностей, подготовка к ЕГЭ - 2019
Теория вероятностей, подготовка к ЕГЭ - 2019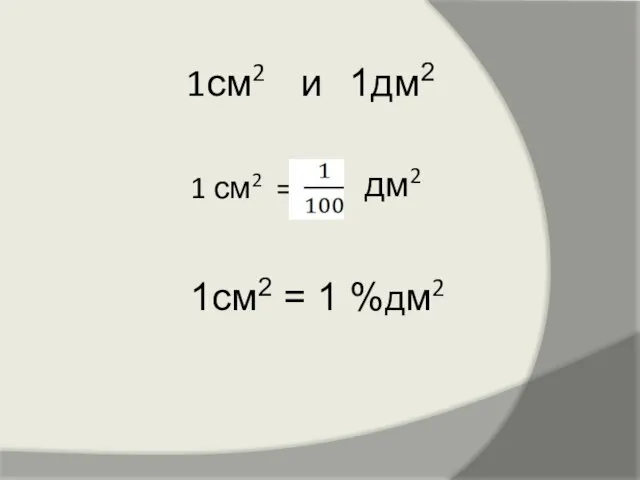 Презентация по математике "Проценты. Сотая часть Вселенной" -
Презентация по математике "Проценты. Сотая часть Вселенной" -  Заряди мозги! По материалам книги: Математика в логических упражнениях Гайштут А.Г
Заряди мозги! По материалам книги: Математика в логических упражнениях Гайштут А.Г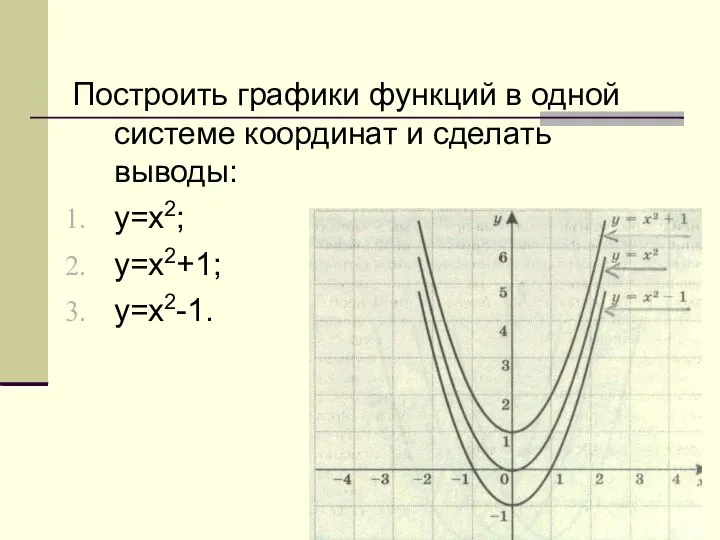 Графики функций в одной системе координат
Графики функций в одной системе координат Время. Йотированные гласные. Решение задач
Время. Йотированные гласные. Решение задач Построение сечений многогранников
Построение сечений многогранников Теорема Фейербаха
Теорема Фейербаха Теорема Пифагора. Домашнее задание
Теорема Пифагора. Домашнее задание Параллельные прямые. Практическая работа
Параллельные прямые. Практическая работа Решаем задачу
Решаем задачу