Содержание
- 2. Для функции многих переменных ее полный дифференциал где - частные производные функции. Это производные по одному
- 3. 2. Интеграл. 2.1 Определенный интеграл Сумму при столь малых , что на каждом из этих интервалов
- 4. 2.2 Неопределенный интеграл Если в задаче необходимо узнать не численный ответ: а саму зависимость , то
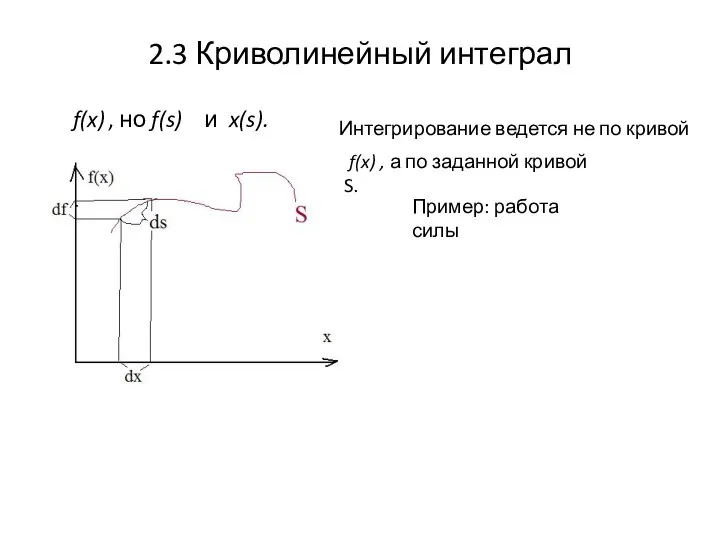
- 5. 2.3 Криволинейный интеграл f(x) , но f(s) и x(s). Интегрирование ведется не по кривой f(x) ,
- 7. Скачать презентацию



 Первообразная. Тренажер
Первообразная. Тренажер Формула Пика
Формула Пика Умножение, деление, возведение в степень рациональных выражений. Тождественные преобразования
Умножение, деление, возведение в степень рациональных выражений. Тождественные преобразования Вычислительная сложность алгоритма
Вычислительная сложность алгоритма Постер-фракталы для интерьера
Постер-фракталы для интерьера Биржа знаний
Биржа знаний Нахождение 2 чисел по их сумме и разности (в мире животных и птиц). Урок 2
Нахождение 2 чисел по их сумме и разности (в мире животных и птиц). Урок 2 Косинус острого угла прямоугольного треугольника. 8 класс
Косинус острого угла прямоугольного треугольника. 8 класс Пределы. Раскрытие неопределенности. 2 часть
Пределы. Раскрытие неопределенности. 2 часть Основное свойство дроби
Основное свойство дроби Считаем со Смешариками (1 класс)
Считаем со Смешариками (1 класс) Великие математики
Великие математики Тестирование
Тестирование Преобразование выражения A sin x + B cos х к виду С sin(x+t)
Преобразование выражения A sin x + B cos х к виду С sin(x+t)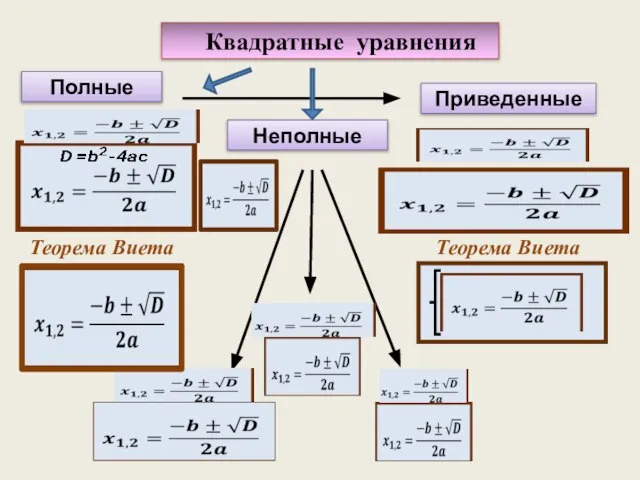 Квадратные уравнения
Квадратные уравнения Последовательности. Способы задания и свойства
Последовательности. Способы задания и свойства Симметрия-асимметрия
Симметрия-асимметрия Типы моделей процессов и систем
Типы моделей процессов и систем Математика вокруг нас. Геометрические узоры и орнамент на посуде
Математика вокруг нас. Геометрические узоры и орнамент на посуде Комбинированный урок
Комбинированный урок Задания Кириллу
Задания Кириллу Выбор схемы измерения переменных
Выбор схемы измерения переменных Решение задач
Решение задач Презентация на тему Мнимая единица
Презентация на тему Мнимая единица  Эллипсоид — поверхность в трёхмерном пространстве
Эллипсоид — поверхность в трёхмерном пространстве Подобные треугольники
Подобные треугольники Свойства функций
Свойства функций Способы извлечения квадратных корней из многозначных чисел без калькулятора
Способы извлечения квадратных корней из многозначных чисел без калькулятора