k последних столбцов, k первых и k последних строк, называется k-м субрезультантом полиномов f и g и обозначается R(k)(f, g).
ТЕОРЕМА 5: А) Для существования d общих корней f(x) и g(x) (т.е. для того, чтобы deg(НОД (f, g)) = d), необходимо и достаточно, чтобы R(f, g) = R(1)(f, g) = ... = R(d−1)(f, g) = 0, R(d)(f, g) ≠ 0.
б) В этом случае НОД(f, g) можно представить в виде xdR(d)(f,g) + xd−1 det Md(1) + ... + det M(d)
в) Полиномы v(x) и u(x), дающие линейное представление НОД(f, g), получаются из R(d) заменой в нем последнего столбца на [xm−d−1, xm−d−2, . . ., x, 1, 0, 0,..., 0] и [0, 0,..., 0, 0, 1, x, . . ., xn−d−1] соответственно. Эти полиномы будут единственными при ограничениях на степени: deg v ≤ m − d − 1, deg u ≤ n − d − 1 .













 Действия с действительными числами
Действия с действительными числами арифметический корень (1)
арифметический корень (1) Квадратичная функция
Квадратичная функция Применение производной к исследованию функций
Применение производной к исследованию функций Оценка существенности уравнения регрессии и его параметров
Оценка существенности уравнения регрессии и его параметров Нахождение неизвестного числа в равенствах вида
Нахождение неизвестного числа в равенствах вида Плоскость в пространстве
Плоскость в пространстве Роль и место математики в современном мире. Пределы. Свойства пределов. Тема 1.1
Роль и место математики в современном мире. Пределы. Свойства пределов. Тема 1.1 Математическая разминка
Математическая разминка Сокращение дробей
Сокращение дробей Измеряй и сравнивай
Измеряй и сравнивай Algebraic constructions generated by causal structure of space-times
Algebraic constructions generated by causal structure of space-times Свойства бинарных отношений
Свойства бинарных отношений Планиметрия (по материалам открытого банка задач ЕГЭ по математике (профильный уровень)
Планиметрия (по материалам открытого банка задач ЕГЭ по математике (профильный уровень) Презентация по математике "Величины. Масса" -
Презентация по математике "Величины. Масса" -  Откроем для себя мир загадок нашей планеты!
Откроем для себя мир загадок нашей планеты! Медианы, биссектрисы и высоты треугольника
Медианы, биссектрисы и высоты треугольника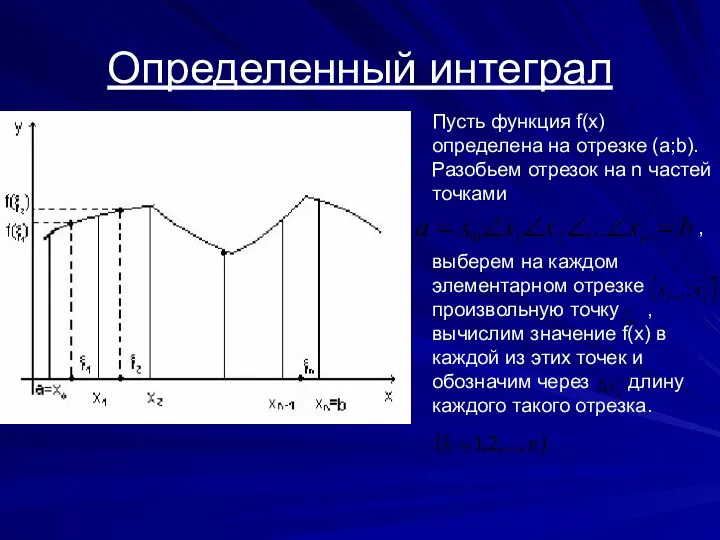 Определенный интеграл
Определенный интеграл Деление на 4
Деление на 4 Определение и содержание математического программирования как математической дисциплины
Определение и содержание математического программирования как математической дисциплины Генеральная совокупность и выборка
Генеральная совокупность и выборка Подготовка к экзамену. Решение уравнений и неравенств
Подготовка к экзамену. Решение уравнений и неравенств Сечение многогранника плоскостью
Сечение многогранника плоскостью Звёздный час дроби. Внеклассное мероприятие для 5 класса. Конкурсная работа
Звёздный час дроби. Внеклассное мероприятие для 5 класса. Конкурсная работа Инфекционные заболевания, их классификация и профилактика
Инфекционные заболевания, их классификация и профилактика Устный счет
Устный счет Зависимость в математике
Зависимость в математике Параметрические характеристики параболы
Параметрические характеристики параболы