Способы решения систем уравнений

Различные способы решения систем уравнений
метод подстановки
метод сложения
метод введения новых переменных
графический метод

Метод подстановки
Одно из уравнений системы преобразуют к виду, в котором y выражено через х ( или х через y )
Полученное выражение подставляют вместо y (или вместо х ) во второе уравнение. В результате получается уравнение с одной переменной
Находят корни этого уравнения
Воспользовавшись выражением y через х(или х через y), находят соответствующие значения х (или y)

Метод сложения
Преобразовать коэффициенты так, чтобы коэффициенты при х или у были противоположными числами
Сложить получившиеся уравнения
Решить уравнение с одной переменной

Метод введения новых переменных
Замени одно или два выражения в уравнениях системы новыми переменными так, чтобы вновь полученные уравнения стали более простыми.
Реши полученную систему уравнений методам наиболее подходящим для э той системы уравнений.
Сделай обратную замену, для того, чтобы найти значения первоначальных переменных.
Запиши ответ в виде пар значений (x,y), которые были найдены на третьем шаге.

Графический метод
Выразить в обоих уравнениях системы переменную у через переменную х
Построить графики функций в одной
системе координат.
Отметить точки пересечения графиков, выписать их координаты.
Записать в ответ полученные пары
чисел (х;у).

Способ подстановки
Решить систему уравнений:
Решение:
xy = -3;

Если z =9, то ,
z =1, то
-3,-1,1,3 отличны от нуля, значит, они являются корнями уравнения:
Ответ: (3;-1), (-3;1), (-1;3), (1;-3)

Метод сложения
Решить систему уравнений:
Умножу первое уравнение системы на число 2,
а второе на число -3, получу
Сложу уравнение системы:
Решу уравнение:
Подставлю найденное число вместо n в первое уравнение исходной системы:
Решу уравнение относительно m:
Система имеет одно решение: (-0,5;1)
Ответ: (-0,5;1)

Преимущества и недостатки метода
Преимущества:
Систему уравнений легче решать методом сложения, когда коэффициенты при X и Y сразу являются противоположными числами.
Метод позволяет быстро исключить одну из неизвестных переменных и найти другую.
Недостатки:
Метод сложения невозможно применить,когда у переменных в двух уравнениях разные
показатели степени.

Метод введения новых переменных
Пусть
и учитывая, что
получим:
Если u=-3, то
или
Тогда получим:
и
Полученные системы тоже являются симметричными системами, которые уже решали.
Итак, (3;1), (-1;3), (-3;1),(1;-3) - решения данной системы.

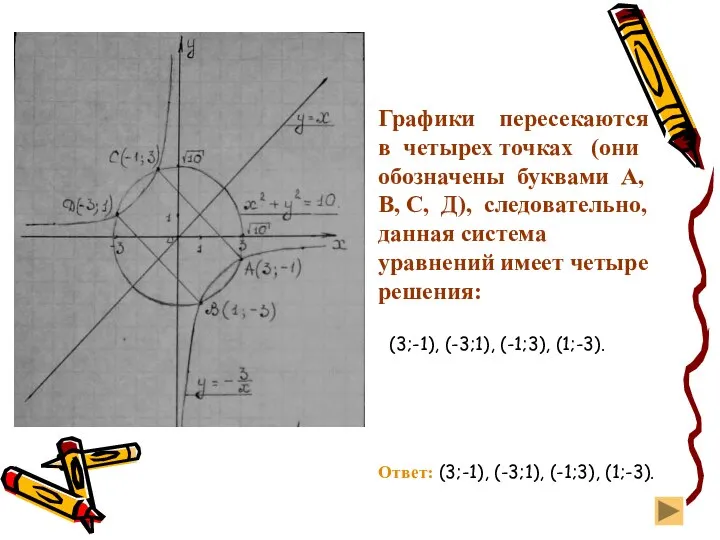
Графический способ
Графиком уравнения является окружность с центром в точке (0;0) и радиусом
В одной системе координат построим графики уравнений: ху= -3 и
Графиком уравнения ху=-3 является гипербола, ветви которой расположены во II и IV координатных четвертях.

Графики пересекаются в четырех точках (они обозначены буквами А, В, С, Д), следовательно, данная система уравнений имеет четыре решения:
(3;-1), (-3;1), (-1;3), (1;-3).
Ответ: (3;-1), (-3;1), (-1;3), (1;-3).

Графический метод решения систем, как и графический метод решения уравнений, красив, но ненадежен:
во-первых, потому, что графики уравнений мы сумеем построить далеко не всегда;
во-вторых, даже если графики уравнений удалось построить, точки пересечения могут быть не такими «хорошими», как в специально подобранных примерах учебника, а то и вовсе могут оказаться за пределами чертежа.
Преимущества и недостатки метода

Проверь себя
Реши систему уравнений, используя метод подстановки:
Реши систему уравнений, используя метод сложения:
Реши систему уравнений , используя графический способ:
Реши систему уравнений, используя метод подстановки: