Содержание
- 2. Задачи: Найти необходимую литературу и изучить её Научиться решать задачи этими способами Научить одноклассников использовать эти
- 3. Объект исследования: Способы решения задач Методы исследования: Работа с литературой; Анализ; Обобщение; Сравнение; Предмет исследования: Алгоритм
- 4. Способы решения задач на смеси и сплавы Решение задач с помощью формулы Решение задач с помощью
- 5. Решение задач с помощью формулы Пример 1: В сосуд, содержащий 5 литров 26-процентного водного раствора некоторого
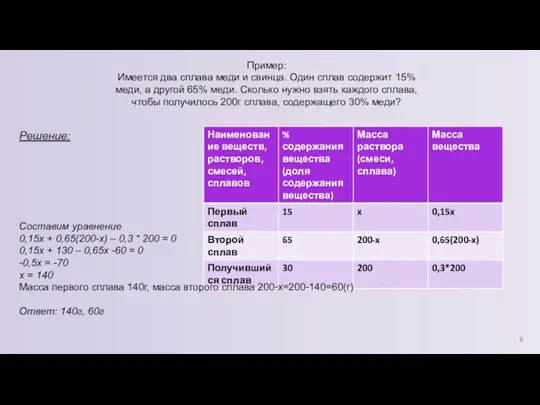
- 6. Пример: Имеется два сплава меди и свинца. Один сплав содержит 15% меди, а другой 65% меди.
- 7. Табличный способ Для того, чтобы решить данный вид задач с помощью таблицы надо: - составить и
- 8. Пример: Имеется два сплава меди и свинца. Один сплав содержит 15% меди, а другой 65% меди.
- 9. Решение задач с помощью модели-схемы Изобразим каждый из сплавов в виде прямоугольника, разбитого на два фрагмента
- 10. Теперь заполняем получившиеся прямоугольники в соответствии с условием задачи: Над каждым прямоугольником («маленьким») указываем соответствующие компоненты
- 11. Пример: В 4кг сплава меди и олова содержится 40% олова. Сколько килограммов олова надо добавить к
- 12. Старинный способ решения задач на смеси и сплавы («метод рыбки»)
- 13. Пример: Имеется склянка 20%-го раствора кислоты и склянка 40%-го раствора кислоты. Смешали 200 г раствора из
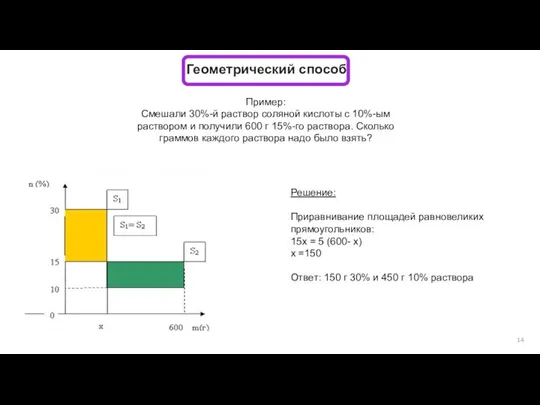
- 14. Геометрический способ Пример: Смешали 30%-й раствор соляной кислоты с 10%-ым раствором и получили 600 г 15%-го
- 15. Правило креста
- 16. Пример: Смешали некоторое количество 11-процентного раствора некоторого вещества с таким же количеством 17-процентного раствора этого вещества.
- 17. Применяем формулу: Масса смеси * концентрацию = количество чистого вещества 5 * 0,12 = 0,6 масса
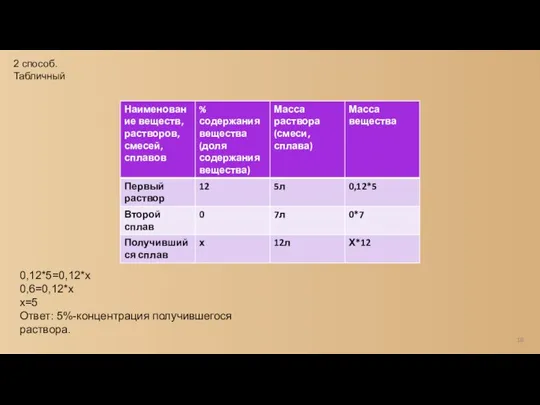
- 18. 18 2 способ. Табличный 0,12*5=0,12*х 0,6=0,12*х x=5 Ответ: 5%-концентрация получившегося раствора.
- 19. 19 0,12*5+0*7=12y 0,6=12y y=0,05*100%=5% Ответ: 5%-концентрация получившегося раствора. 3 способ. Модель схема (12-y)*5=7y 60-5y=7y 12y=60 y=5%
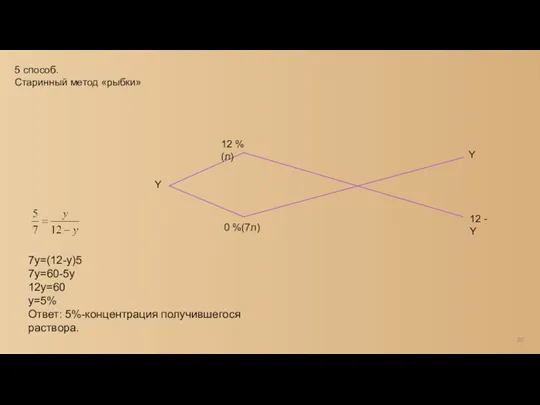
- 20. 20 5 способ. Старинный метод «рыбки» Y 12 % (л) 0 %(7л) Y 12 - Y
- 21. 21 7y=(12-y)5 7y=60-5y 12y=60 y=5% Ответ: 5%-концентрация получившегося раствора. 6 способ. Способ креста
- 22. 22 Список литературы https://infourok.ru/sposobi-resheniya-zadach-na-rastvori-smesi-i-splavi-966187.html https://kopilkaurokov.ru/matematika/presentacii/razlichnyie-sposoby-rieshieniia-zadach-na-smiesi-splavy-rastvory
- 24. Скачать презентацию
















 Подготовка к контрольной работе
Подготовка к контрольной работе Равносильность неравенств
Равносильность неравенств Применение интеграла к вычислению площадей
Применение интеграла к вычислению площадей Нефть. Добыча, переработка, использование. Задачи на нахождение объёма цилиндра. Работа с формулами в таблице Excel
Нефть. Добыча, переработка, использование. Задачи на нахождение объёма цилиндра. Работа с формулами в таблице Excel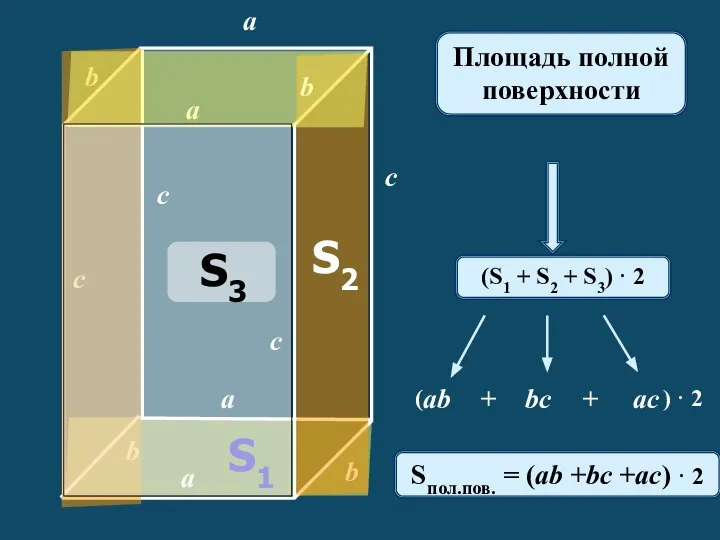 Площадь полной поверхности
Площадь полной поверхности Повторение. Урок для 8 класса
Повторение. Урок для 8 класса Уравнения и неравенства с одной переменной
Уравнения и неравенства с одной переменной Вводная лекция. Урок 1
Вводная лекция. Урок 1 Случаи сложения и вычитания, основанные на знаниях нумерации
Случаи сложения и вычитания, основанные на знаниях нумерации Геометрия и искусство
Геометрия и искусство История создания числа 2
История создания числа 2 Построение сечений
Построение сечений Индивидуальный итоговый проект по математике 22 задание ОГЭ
Индивидуальный итоговый проект по математике 22 задание ОГЭ Теория принятия решений. Вопросы к экзамену
Теория принятия решений. Вопросы к экзамену Цилиндр. Сечения цилиндра
Цилиндр. Сечения цилиндра Логика и математическая логика. История логики. Алгебра высказываний
Логика и математическая логика. История логики. Алгебра высказываний Четырехугольники. Параллелограмм
Четырехугольники. Параллелограмм Пирамида и ее элементы. Правильная пирамида
Пирамида и ее элементы. Правильная пирамида Математический КВН
Математический КВН Умножение дробей на натуральное число
Умножение дробей на натуральное число Решение задач на применение аксиом стереометрии и их следствий
Решение задач на применение аксиом стереометрии и их следствий Схемотехника
Схемотехника Применение осевой симметрии в жизни
Применение осевой симметрии в жизни Известное и неизвестное
Известное и неизвестное Сложение и вычитание смешанных чисел. Подготовка к контрольной работе
Сложение и вычитание смешанных чисел. Подготовка к контрольной работе Презентация на тему ПРОИЗВОДНАЯ СТЕПЕННОЙ ФУНКЦИИ
Презентация на тему ПРОИЗВОДНАЯ СТЕПЕННОЙ ФУНКЦИИ  Алгоритм сложения и вычитания двузначных чисел 32 + 45, 77 – 32
Алгоритм сложения и вычитания двузначных чисел 32 + 45, 77 – 32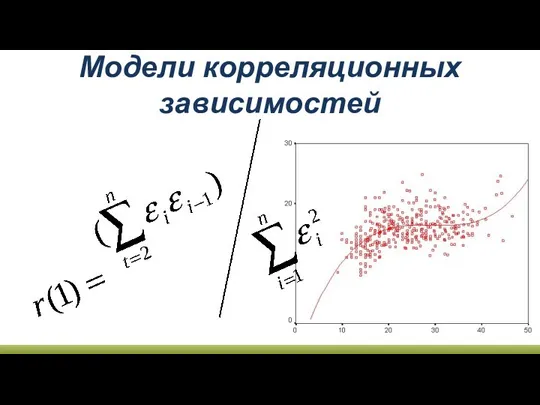 Модели корелляционных зависимостей
Модели корелляционных зависимостей