Способы задания плоскости

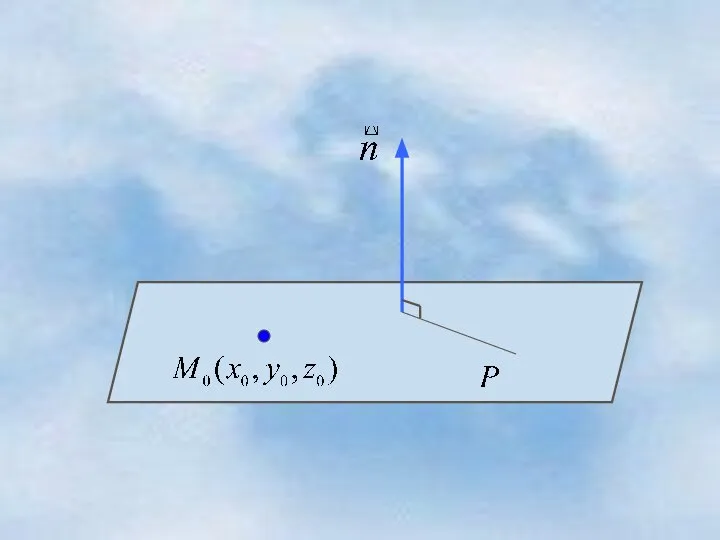
Выберем на плоскости произвольную точку
Тогда
и
Распишем его в координатах:
Тогда скалярное произведение этих векторов должно быть равно нулю:

уравнение плоскости, проходящей
через заданную точку и перпендикулярной
заданному вектору
1

Раскроем скобки в уравнении (1):
Обозначим:
2. Общее уравнение плоскости

общее уравнение плоскости
2

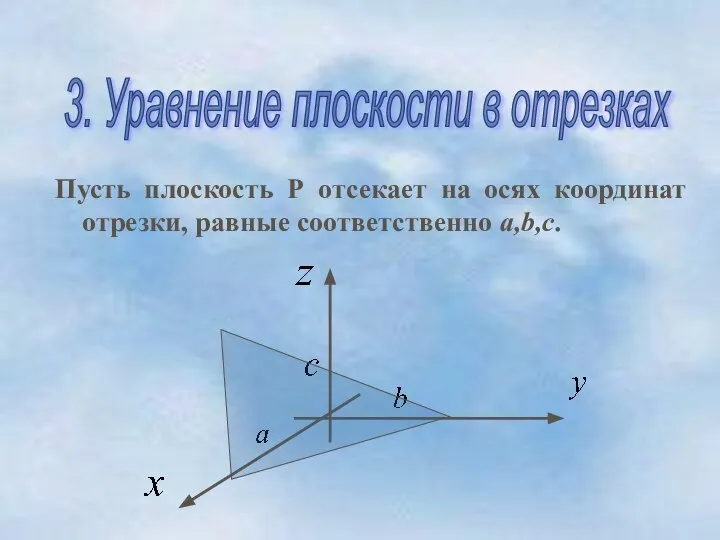
Пусть плоскость Р отсекает на осях координат отрезки, равные соответственно a,b,c.
3. Уравнение плоскости в отрезках

уравнение плоскости в отрезках
3

4. Уравнение плоскости, проходящей
через три точки
Пусть задана плоскость, проходящая через три точки:
Тогда уравнение этой плоскости можно записать в виде равенства нулю определителя:

уравнение плоскости, проходящей
через три точки
4

Условия параллельности и перпендикулярности плоскостей определяются условиями коллинеарности и перпендикулярности их нормальных векторов:
Пусть даны две плоскости с нормальными векторами

Условие параллельности
двух плоскостей

Условие перпендикулярности
двух плоскостей

И плоскость
Пусть дана точка
Тогда расстояние от точки до плоскости определяется по формуле: