Справедливые и несправедливые игры с точки зрения теории вероятностей

Подготовили: Швецова Юлия, Позднякова
Анастасия, Караваннова Ирина
9 «в» класс, МБОУ СШ №12

Понятие вероятности:
Вероятность события– это численная мера объективной возможности его появления.
Вероятностью наступления случайного события называется отношение m/n, где n – число всех возможных исходов эксперимента, а m – число всех благоприятных исходов:
Р(А)= m/n.

Пример.
Бросаем монетку. Найти вероятность выпадения орла.
Возможно два исхода: орел и решка; благоприятный один – орел, значит вероятность выпадения орла равна ½.

Справедливыми играми называются игры, в которых игроки имеют равные шансы на победу.
В несправедливых играх шансы игроков разные.
Шанс – это вероятность выигрыша

Задача1. Выясним, является ли справедливым выбор преимущества между двумя игроками с помощью выбора случайным образом одной карты красной или черной масти.

Решение:
Колода карт содержит 36 карт, из которых 18 красной масти и столько же черной. Значит, вероятность того что игрок вытянет карту красной масти равна 18/36, то есть ½. Вероятность вытянуть черную масть так же ½. Вероятности (шансы) равны, этот выбор справедлив.

Задача2.
В одной комнате студенческого общежития живут Антон, Борис и Василий. Нужно регулярно назначать дежурного по комнате. Юноши подбрасывают две монеты и в зависимости от результата определяют дежурного:
- если выпали орел и решка, дежурит Антон,
- если выпали два орла, дежурит Борис,
- если выпали две решки, дежурит Василий.

Справедлив ли такой подход к выбору дежурного?
Составим таблицу исходов:

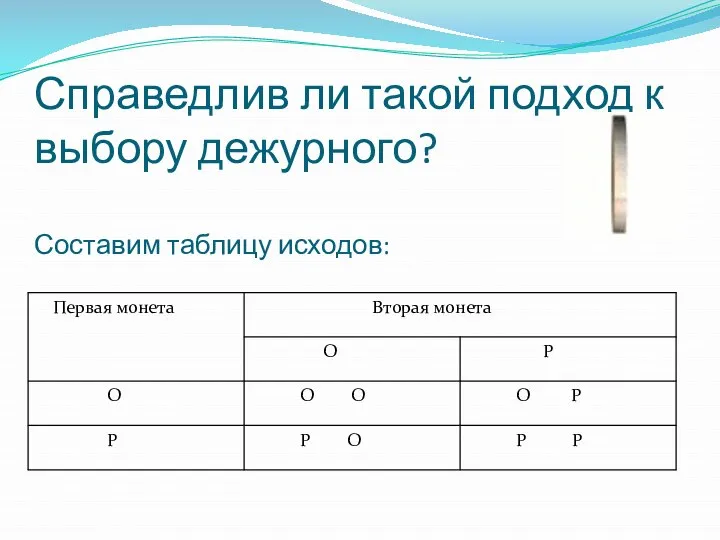
Такой подход не является справедливым, так как вероятность появления орла и решки больше, а вероятность выпадения двух решек или двух орлов одинакова. Можно сказать, что Антону, по всей вероятности, придется в два раза чаще дежурить, чем каждому из его друзей.

Задача3.
Докажем, что выбор преимущества между двумя играющими с помощью игры «Камень-ножницы-бумага» является справедливым.
К – камень, Н – ножницы, Б – бумага.

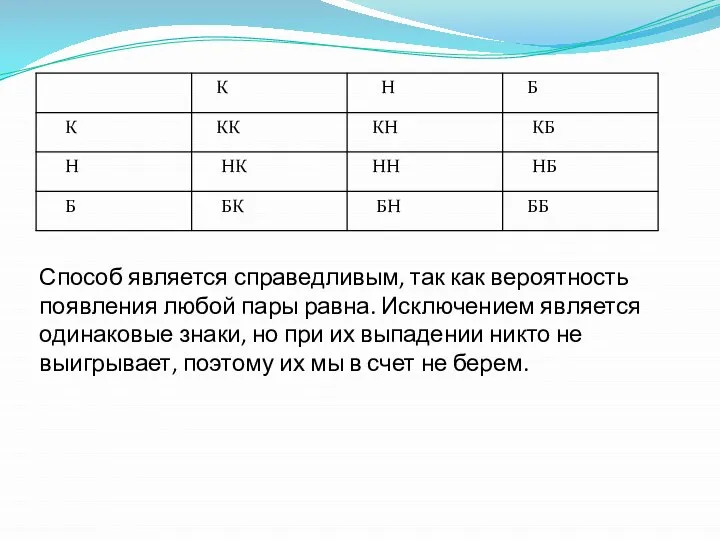
Способ является справедливым, так как вероятность появления любой пары равна. Исключением является одинаковые знаки, но при их выпадении никто не выигрывает, поэтому их мы в счет не берем.

Соглашаясь на какую-либо игру задумайтесь над своими шансами и над её справедливостью, это поможет вам не обмануться и убережет от нежелательных последствий. Так теория вероятности вам поможет.