Корреляционный анализ в Exel

Что такое корреляционно-регрессионного анализ.
Корреляционно-регрессионный анализ – это один из способов решения задач и поиска информации.
Он позволяет определить совместное влияние множества взаимосвязанных и единовременно действующих признаков, а также отдельное влияние каждого признака на экономическое явление (процесс).

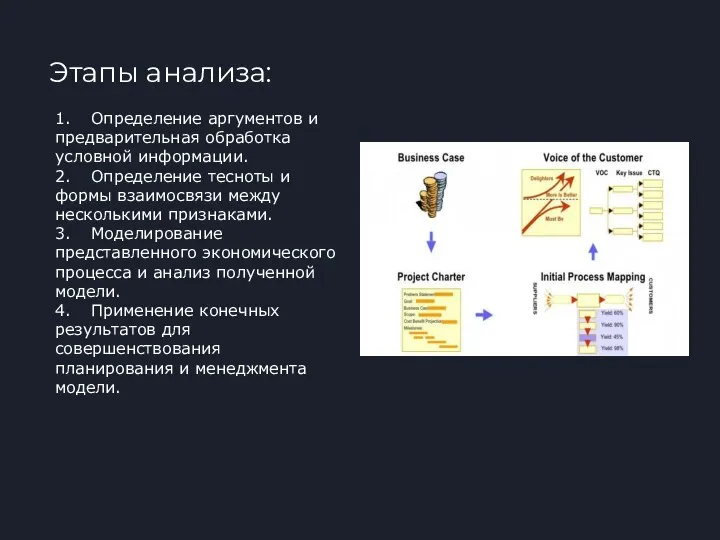
Этапы анализа:
1. Определение аргументов и предварительная обработка условной информации.
2. Определение тесноты и формы взаимосвязи между несколькими признаками.
3. Моделирование представленного экономического процесса и анализ полученной модели.
4. Применение конечных результатов для совершенствования планирования и менеджмента модели.

Корреляционно-регрессионный анализ по вот таким сложным формулам:
Парные коэффициенты корреляции
С помощью парного линейного коэффициента корреляции выявляется связь между двумя признаками, один из которых можно рассматривать как результативный, другой — как факторный. Но в действительности на результат воздействуют несколько факторов.

Частный, или чистый, коэффициент корреляции
остаточная дисперсия(остаточная сумма квадратов) = S2

Если выразить остаточную дисперсию через показатель детерминации S2 остат = sigma2у*(1 - r2), то формула коэффициента частной корреляции примет вид:

Коэффициент множественной корреляции (R) характеризует тесноту связи между результативным показателем и набором фактор¬ных показателей:

• Коэффициенты частной детерминации (показывают влияние вариации аргумента на вариацию искомого признака).
• Коэффициент множественной детерминации (показывает удельный вес всех аргументов на вариацию искомого признака).
• Частные коэффициенты эластичности (характеризуют влияние факторов на результат, выраженное в едином масштабе в процентах).

Цель анализа
Основные задачи корреляционно-регрессионного анализа – это выявление факторов, существенно влияющих на экономический результат явления или процесса, и использование полученной информации для совершенствования планирования экономического процесса или явления.

Также корреляция может изображаться в подобных диаграммах, которые называются решетками
Корреляционная взаимосвязь может иметь один или несколько факторов-признаков, обладать положительной или отрицательной направленностью, быть прямолинейной или криволинейной (в зависимости от выражения).

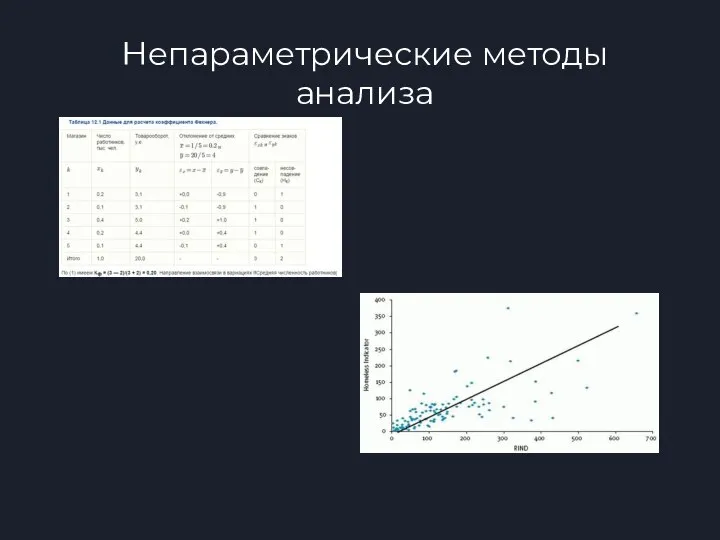
Непараметрические методы анализа
• Коэффициент ранговой корреляции Кендалла (определяет взаимосвязь количественных и качественных значений показателей, в случае если они подлежат ранжированию).
• Коэффициент ранговой корреляции Спирмена (присваивает ранги каждому аргументу и результату, на основе которых определяются разности и вычисляется показатель).
•Коэффициент корреляции знаков Фехнера (определяет количество совпадений и несовпадений отклонений аргументов и результатов от их среднего значения).
Еще один немаловажный метод корреляционно-регрессионного анализа — Метод наименьших квадратов, позволяющий определить аналитическое выражение взаимосвязи результативного признака и его фактора. Он заключается в построении системы уравнений и определении параметров этих уравнений.

Статистические методы
Основой статистических методов корреляционный и регрессионный анализ является один из семи простых инструментов контроля качества - диаграмма разброса (поле корреляции). Этот инструмент позволяет графически отобразить и в дальнейшем проанализировать вид и тесноту связи между исследуемыми факторами.

Для построения поля корреляции, необходимо пройтись по следующим этапам:
1. Сбор не менее 25 пар данных исследуемых параметров в таблицу;
2. Нахождение максимальных и минимальных значений и . Выбор шкалы на горизонтальной и вертикальной оси так, чтобы длины рабочих областей были примерно равны.
3. Построение на отдельном листе координатной плоскости. Если исследуется влияние фактора на показатель качества, то фактор располагают по оси абсцисс, а показатель – по оси ординат; и нанесение собранных пар данных (в случае совпадения точек они либо располагаются максимально близко, либо обозначаются окружностями около первоначальной точки)
4. На диаграмму наносятся все необходимые обозначения:
• название диаграммы;
• интервал времени сбора данных;
• число пар данных;
• название и единицы для каждой оси;
• идентифицирующая информация составителя диаграммы

Если точки корреляционного поля образуют эллипс, главная диагональ которого имеет положительный угол наклона, то имеет место положительная корреляция (пример подобной ситуации можно видеть на рисунке 6.3).
Рис. 6.3. Положительная корреляция

Если точки корреляционного поля образуют эллипс, главная диагональ которого имеет отрицательный угол наклона, то имеет место отрицательная корреляция (пример изображен на рисунке 6.4).
Рис. 6.4. Отрицательная корреляция