Статистический анализ зависимостей между гидрологическими переменными (лекция 11)

Интервальная оценка и оценка значимости
параметров линейной регрессии для двух переменных
В случае, если r не очень велико и длина выборок не превышает 40 лет, то распределение коэффициентов корреляции хорошо аппроксимируется нормальным законом со среднеквадратическим отклонением σ*r,
доверительный интервал для истинного коэффициента корреляции можно представить в виде
r* - t’1- ασr* ≤ r < r*+ t’1- ασr*
где r* - выборочный коэффициент парной корреляции
t’1-α – квантиль стандартного нормального распределения, соответствующий двустороннему уровню значимости 2α

Z – преобразование Фишера
В случае, если значения r>0.4 и n <40, для построения доверительного можно использовать Z – преобразование Фишера, которое связано с r выражением
Z = 0.5 ln[(1+ r)/(1- r)]
В отличие от r статистика Z имеет нормальное распределение даже при n небольшом. СКО для Z определяется по формуле

Последовательность
построения интервальной оценки r при использовании преобразования Фишера
Рассчитывается Z по формуле Z = 0.5 ln[(1+ r)/(1- r)]
Рассчитывается СКО Z по формуле
3. Строиться доверительный интервал для Z
Z* - t’1- ασz* ≤ r < Z* + t’1- ασz*
4. Строиться доверительный интервал для коэффициента корреляции путем обратного перехода от Z к r, т.е.
Здесь z’ = Z* - t’1- ασz* и z’’ = Z* + t’1- ασz*
Z – преобразование Фишера точнее и может быть рекомендовано при любых значениях r>0.4 и n <40
(e2z’ – 1)/(e2z’ + 1) ≤ r < (e2z’’ – 1)/(e2z’’ + 1)

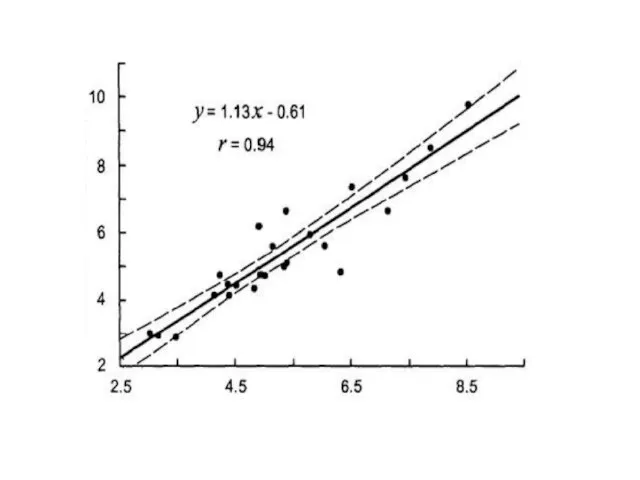
Проверки значимости линейной зависимости между X и Y
Коэффициент корреляции можно использовать для проверки значимости линейной зависимости между X и Y.
В этом случае выдвигается нулевая гипотеза, что r=0, т.е. что связь полностью отсутствует.
Гипотеза опровергается, если
и связь считается статистически значимой.
Если это условие не выполняется, то связь статистически незначима.
Следует иметь в виду, что здесь имеется в виду двусторонний уровень значимости, т.е. вы задаете чему равно 2α, а потом находите α. Допустим, что 2α = 5%, тогда t’1-α = t97,5.

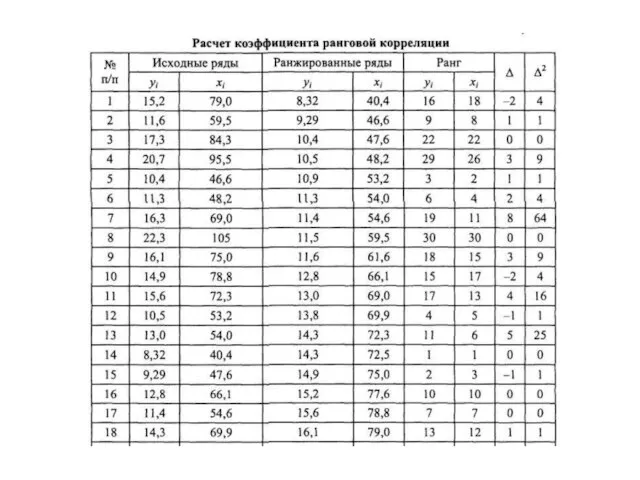
Коэффициент ранговой корреляции Спирмэна
Если распределение случайных рядов y1, y2….yn и x1, x2 …xn существенно отличается от нормального распределения, то для оценки степени их взаимосвязанности можно использовать коэффициент ранговой корреляции Спирмэна rs:
где n – длина выборок;
∆i – разность рангов для пары значений yi и xi
Для коэффициента ранговой корреляции выполняется условие:
-1 ≤ rs ≤ +1
Выдвигается нулевая гипотеза о том, что rs = 0
Гипотеза опровергается, если
(rs)α – критическое значение коэффициента ранговой корреляции при одностороннем уровне значимости α
Для n ≤ 30 значение (rs)α представлены в таблице

Коэффициент ранговой корреляции Спирмэна
При n ≥ 30 величина rs√( n-1) достаточно хорошо описывается нормальным распределением. В этом случае нулевая гипотеза (rs=0) отвергается , если выполняется неравенство
где t’1- α – квантиль стандартного нормального распределения при одностороннем уровне значимости α.

Последовательность расчетов
по методу коэффициента ранговой корреляции Спирмэна
Ряды yi и xi ранжируются в возрастающем порядке
2. Каждому значению yi и xi в ранжированном ряду присваивается порядковый номер (ранг). Самое маленькое значение случайной величины получает первый ранг и т.д.
Каждому значению случайной величины ставится свой ранг
4. Рассчитывается разность рангов yi и xi
5. Рассчитывается квадрат разности рангов ∆2
6. По формуле ниже рассчитывается коэффициент ранговой корреляции
По таблице опред-ся критический коэффициент ранговой корреляции
8. Выдвигается нулевая гипотеза о том, что rs = 0
Гипотеза опровергается, если

Интервальная оценка коэффициента регрессии
Если разброс наблюдений относительно линейной регрессии нормален, то доверительный интервал для коэффициента регрессии имеет вид
где а* - эмпирической значение коэффициента регрессии
σa – стандартная ошибка коэффициента регрессии
t’1-α – квантиль распределения Стьюдента, соответ-щий двухстороннему уровню значимости 2α при числе степеней свободы ν = n - 2
При проверке значимости коэффициента регрессии выдвигается нулевая гипотеза о том, что а=0. Гипотеза опровергается, если
t*а – эмпирическое значение статистики Стьюдента, определяемое по формуле
Если равенство выполняется, то коэффициент регрессии считается статистически значимым, в противном случае коэффициент a* является статистически незначимым и линейная связь между X и Y отсутствует.

Интервальная оценка свободного члена
Доверительный интервал для свободного члена имеет вид
где b* - эмпирической значение коэффициента регрессии
σb – стандартная ошибка коэффициента регрессии
t’1- α – квантиль распределения Стьюдента, соответ-щий двухстороннему уровню значимости 2α при числе степеней свободы ν = n - 2
При проверке значимости коэффициента регрессии выдвигается нулевая гипотеза о том, что b=0. Гипотеза опровергается, если
t*b – эмпирическое значение статистики Стьюдента, определяемое по формуле
Если равенство выполняется, то коэффициент регрессии считается статистически значимым, в противном случае коэффициент b* является статистически незначимым и для аппроксимации зависимости между X и Y вместо выражения
следует использовать выражение

F – критерий значимости регрессии
Часто для проверки значимости линейной регрессии используется критерий
Доказано, что это отношение имеет распределение Фишера со степенями свободы ν1 = 1 и ν2 = n-2. Связь считается значимой, если
где F1- α – теоретическое значение статистики Фишера при уровне значимости α

Построение доверительного
интервала для уравнения регрессии
Доверительные пределы для уравнения регрессии определяются по формуле
- истинное значение случайной величины
- это расчетное значение функции
t’1- α – квантиль распределения Стьюдента, соответствующее двухстороннему уровню значимости 2α при числе степеней свободы ν = n-2
- стандартная ошибка уравнения линейной регрессии