Содержание
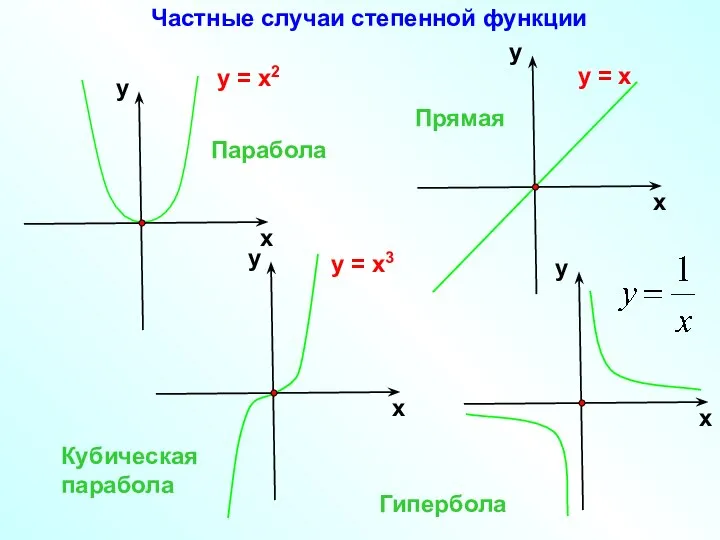
- 2. у = х2 у = х3 Парабола Кубическая парабола Гипербола у = х Прямая Частные случаи
- 3. Функция вида у = хр, где р – действительное число называется степенной функцией Свойства и график
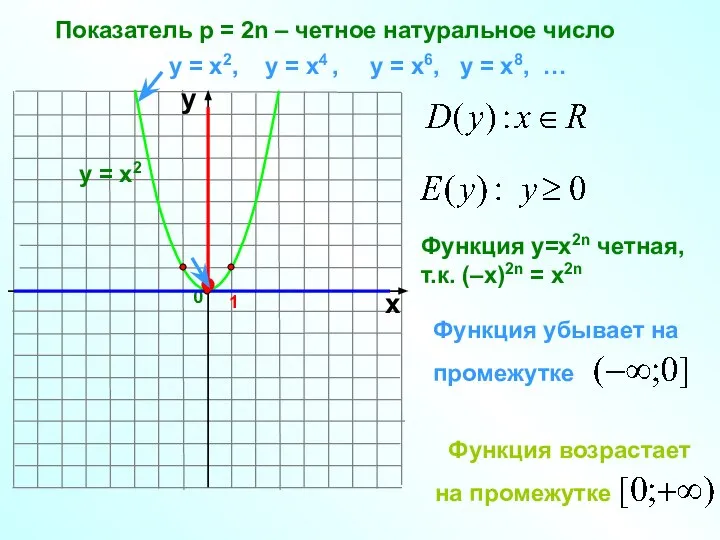
- 4. Показатель р = 2n – четное натуральное число 1 0 х у у = х2, у
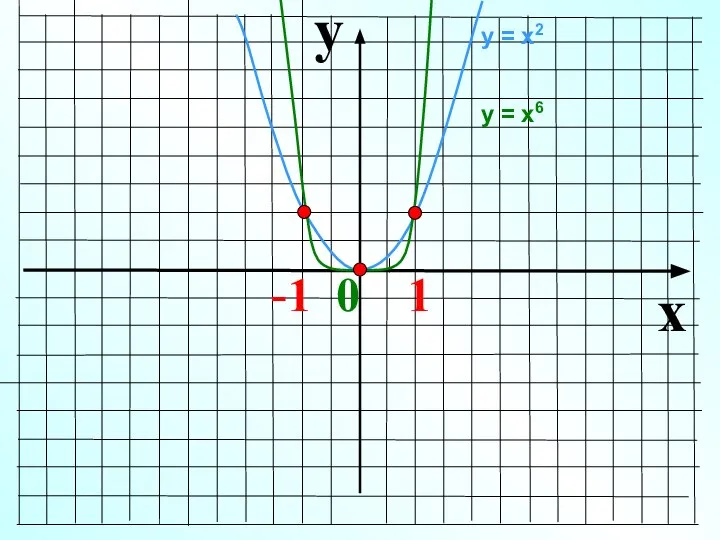
- 5. y x -1 0 1 у = х2 у = х6
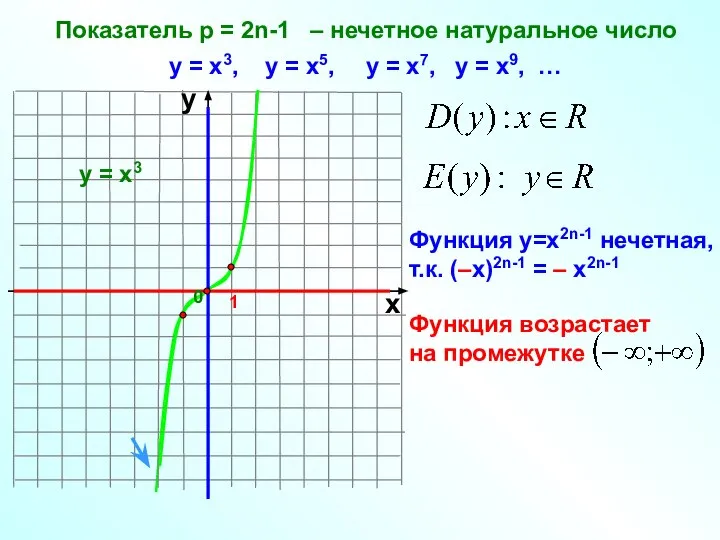
- 6. Показатель р = 2n-1 – нечетное натуральное число 1 х у у = х3, у =
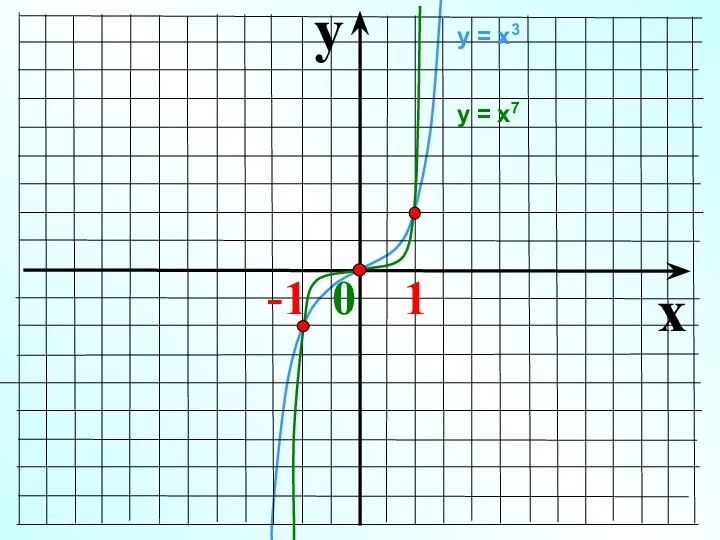
- 7. y x -1 0 1 у = х3 у = х7
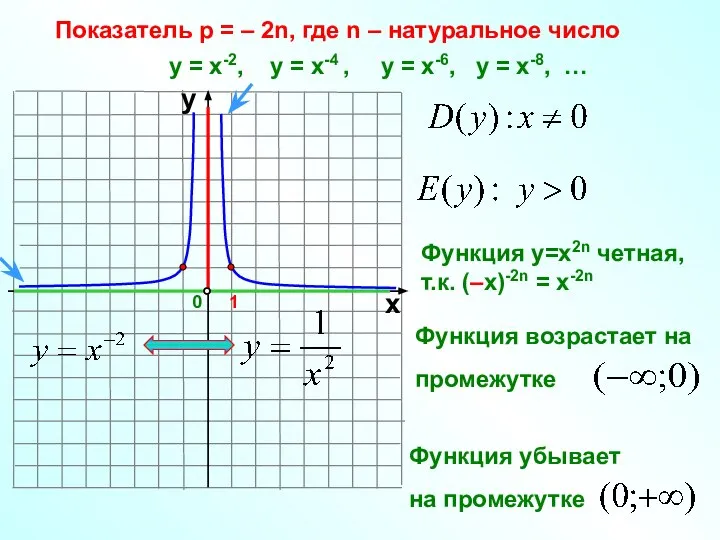
- 8. Показатель р = – 2n, где n – натуральное число 1 0 х у у =
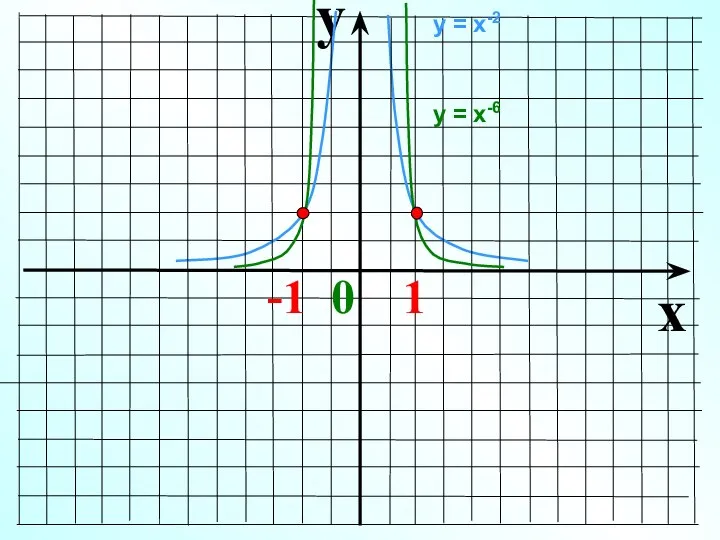
- 9. y x -1 0 1 у = х-2 у = х-6
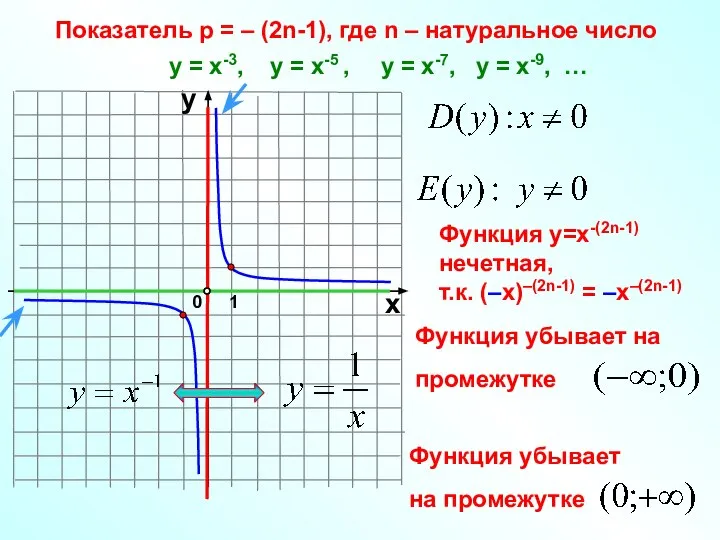
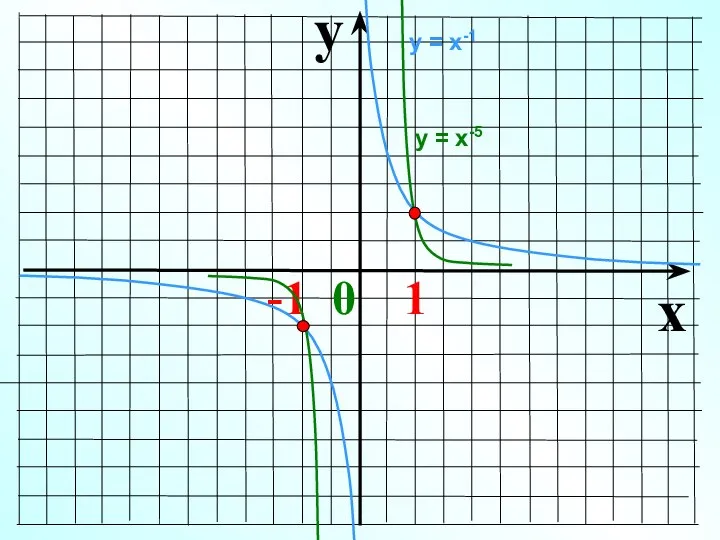
- 10. Показатель р = – (2n-1), где n – натуральное число 1 0 х у у =
- 11. y x -1 0 1 у = х-1 у = х-5
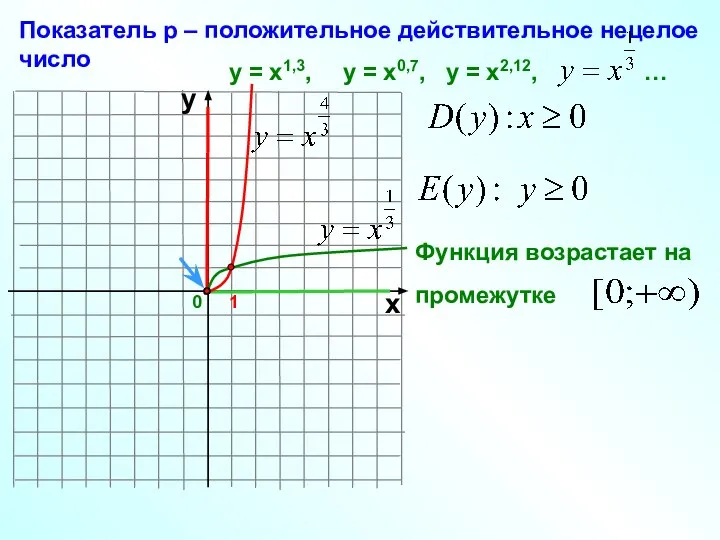
- 12. 0 Показатель р – положительное действительное нецелое число 1 х у у = х1,3, у =
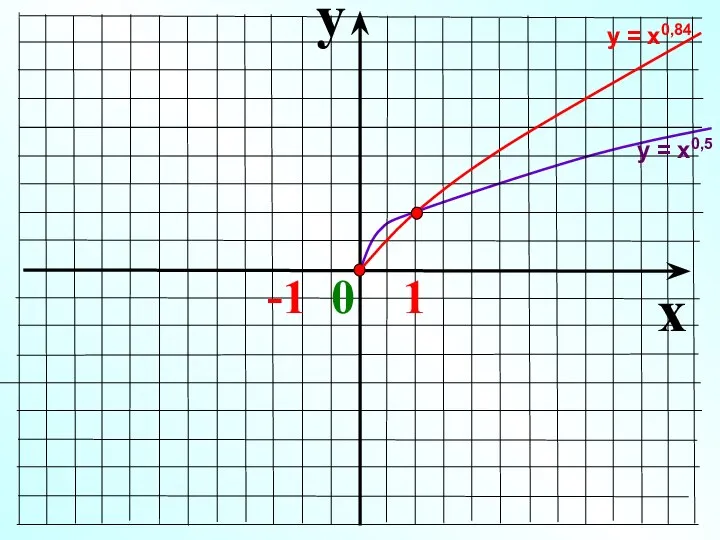
- 13. y x -1 0 1 у = х0,5
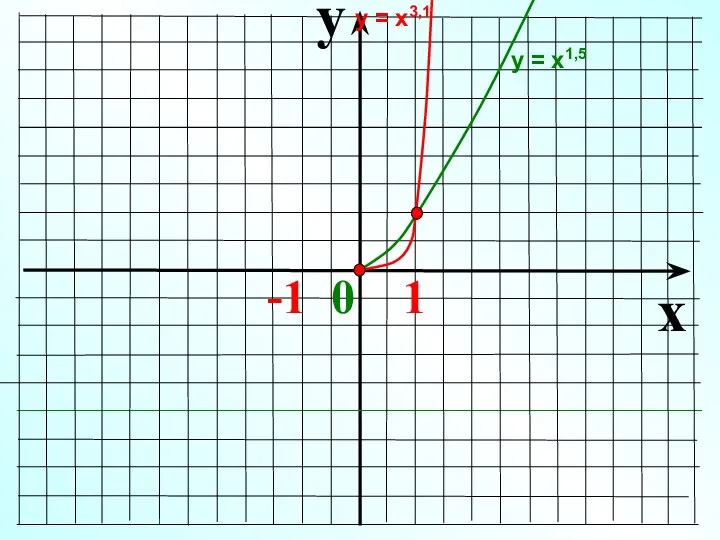
- 14. y x -1 0 1
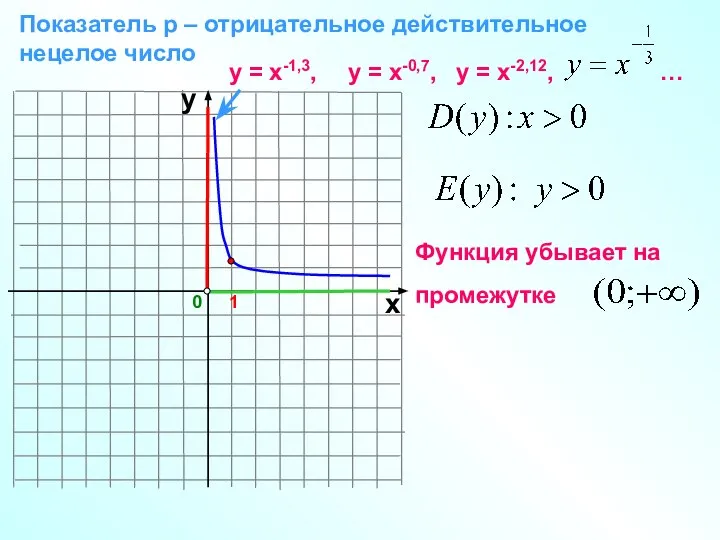
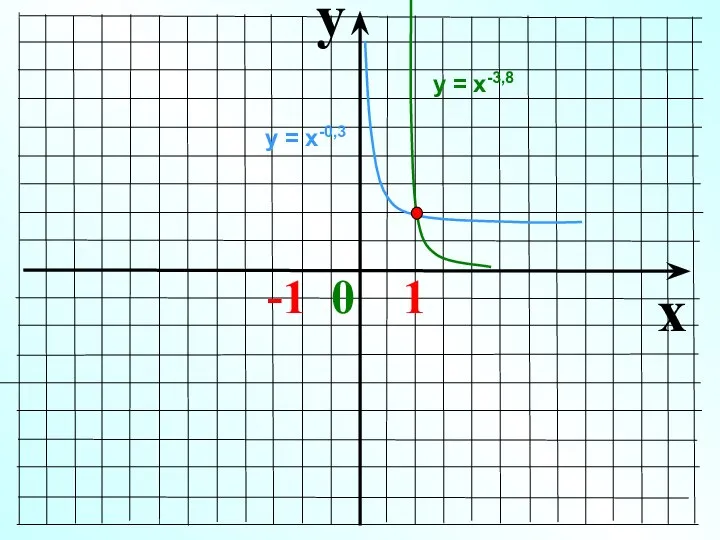
- 15. 0 Показатель р – отрицательное действительное нецелое число 1 х у у = х-1,3, у =
- 16. y x -1 0 1
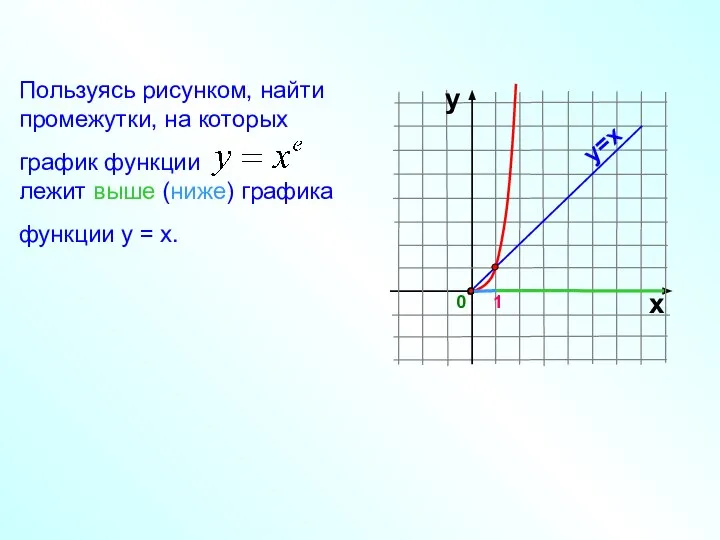
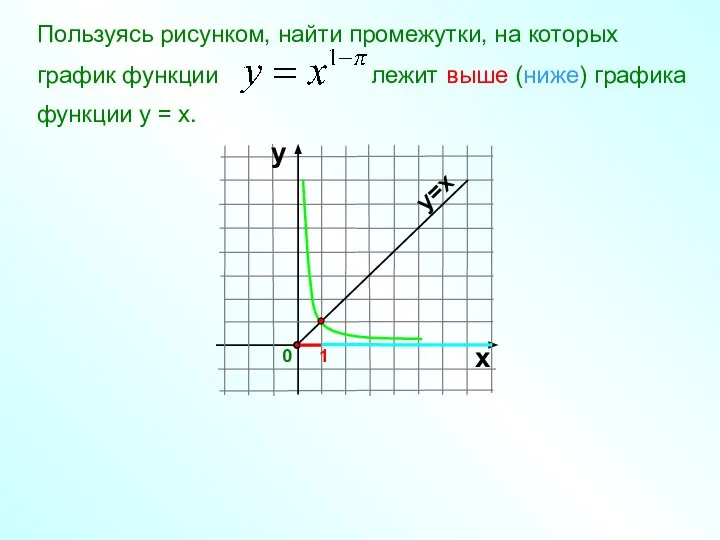
- 17. Пользуясь рисунком, найти промежутки, на которых график функции лежит выше (ниже) графика функции у = х.
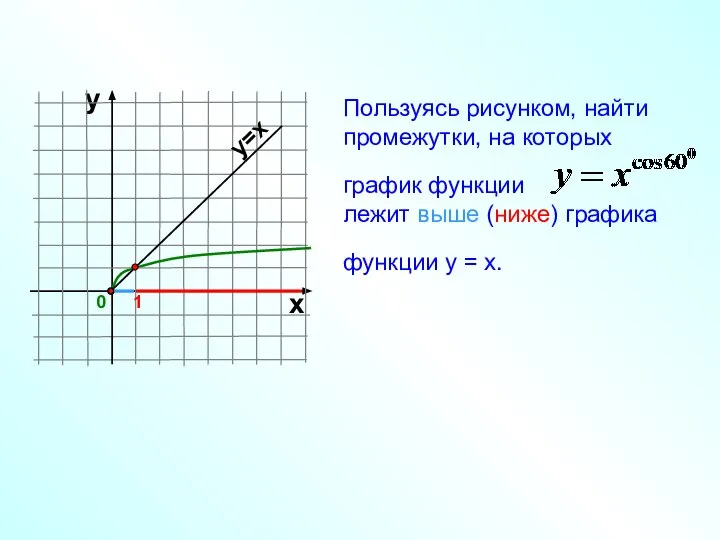
- 18. Пользуясь рисунком, найти промежутки, на которых график функции лежит выше (ниже) графика функции у = х.
- 19. Пользуясь рисунком, найти промежутки, на которых график функции лежит выше (ниже) графика функции у = х.
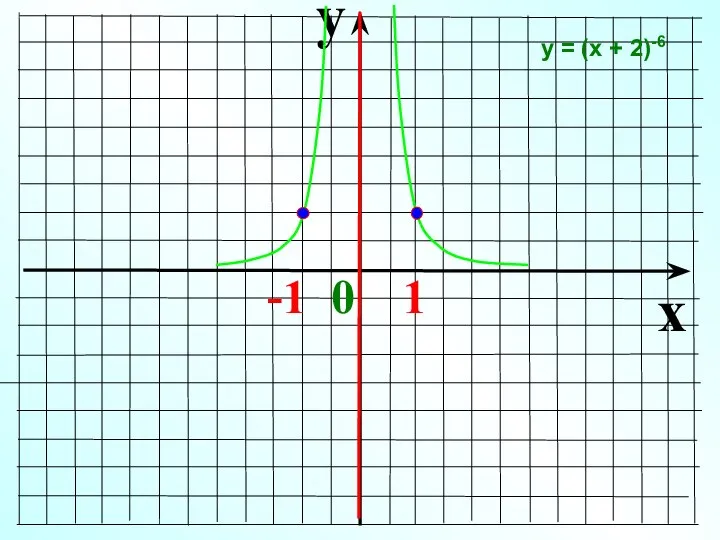
- 20. y x -1 0 1 у = (х + 2)-6
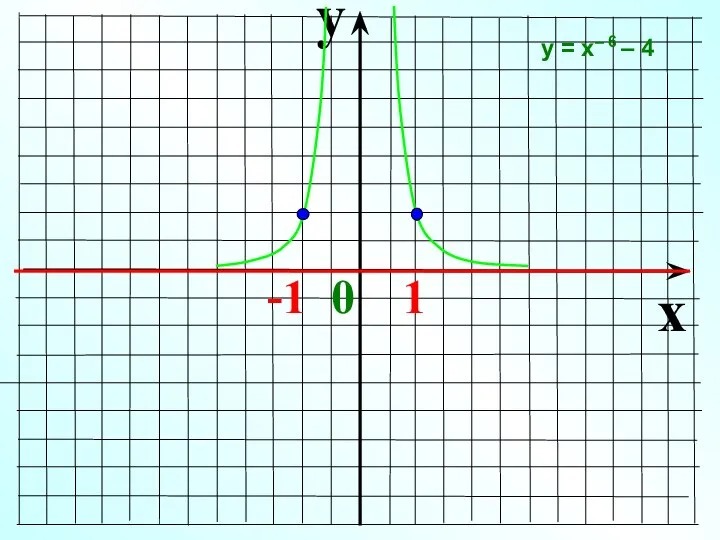
- 21. y x -1 0 1 у = х– 6 – 4
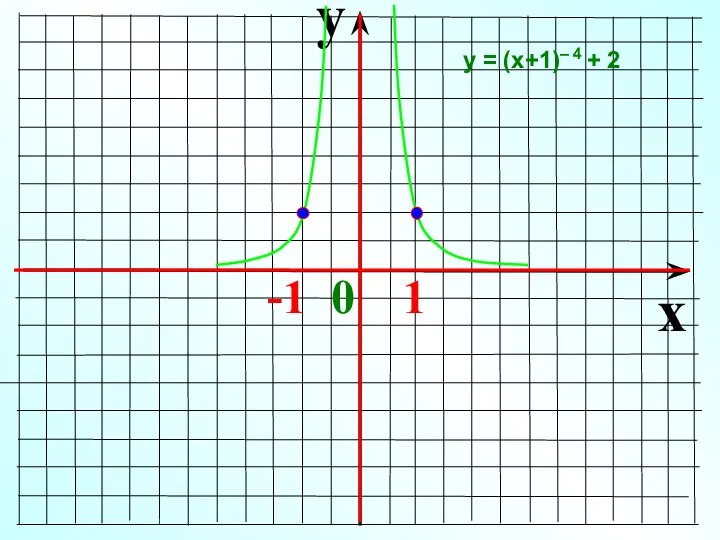
- 22. y x -1 0 1 у = (х+1)– 4 + 2
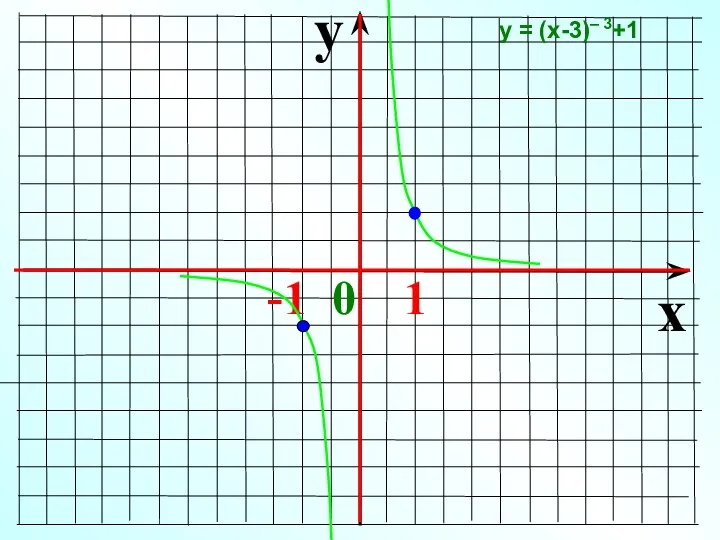
- 23. y x -1 0 1 у = (х-3)– 3+1
- 25. Скачать презентацию

 Устные и письменные приемы вычислений
Устные и письменные приемы вычислений Нахождение наибольшего и наименьшего значений функции
Нахождение наибольшего и наименьшего значений функции Примеры
Примеры Элементы теории фредгольмовых отображений
Элементы теории фредгольмовых отображений Параллельные и перпендикулярные прямые
Параллельные и перпендикулярные прямые Разложение вектора по базису
Разложение вектора по базису Цилиндр. 11 класс
Цилиндр. 11 класс Метод моментов решений различных классов дифференицальных и интегральных уравнений
Метод моментов решений различных классов дифференицальных и интегральных уравнений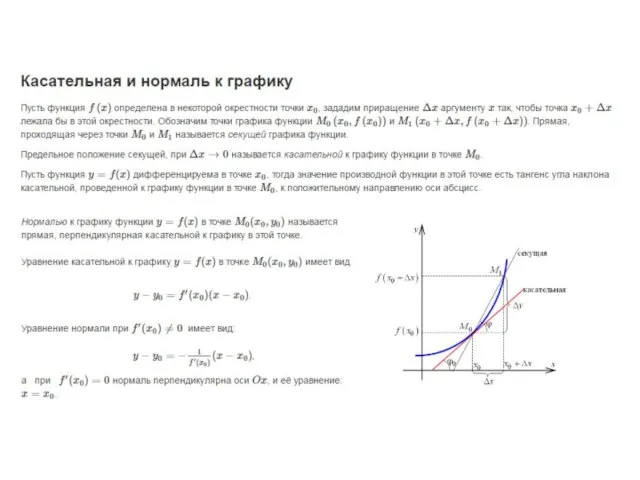 Касательная и нормаль к графику
Касательная и нормаль к графику Решение систем с неизвестными множествами
Решение систем с неизвестными множествами Система линейных уравнений. 7 класс
Система линейных уравнений. 7 класс Сравнение чисел. 1 класс
Сравнение чисел. 1 класс Произведение дробей, обратных друг другу
Произведение дробей, обратных друг другу Сечение поверхности плоскостью
Сечение поверхности плоскостью Конфетное вычитание
Конфетное вычитание Линейное программирование
Линейное программирование Буквенные выражения. Уравнения. Математический диктант
Буквенные выражения. Уравнения. Математический диктант 3.3. Понятие функции
3.3. Понятие функции Положительные и отрицательные числа ( 6 класс )
Положительные и отрицательные числа ( 6 класс ) Принак подобия треугольников. Урок 33
Принак подобия треугольников. Урок 33 Юность Великих математиков. 5 класс
Юность Великих математиков. 5 класс Построение графика у=f(x)
Построение графика у=f(x) Тригонометрия. Радианная мера угла. Соответствие радианной и градусной мер углов
Тригонометрия. Радианная мера угла. Соответствие радианной и градусной мер углов Частное целых чисел. 6 класс
Частное целых чисел. 6 класс Презентация на тему Вертикальные и смежные углы
Презентация на тему Вертикальные и смежные углы  Шаблон презентации по математике
Шаблон презентации по математике Перпендикулярность прямых и плоскостей
Перпендикулярность прямых и плоскостей Полное исследование функций и построение их графиков
Полное исследование функций и построение их графиков