Содержание
- 2. Определение функции. Обозначение функции.
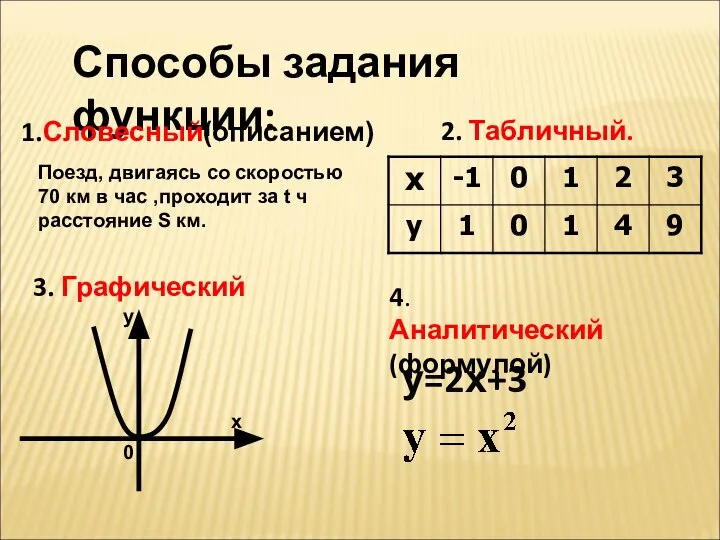
- 3. Способы задания функции: 1.Словесный(описанием) 2. Табличный. 3. Графический 4. Аналитический (формулой) у=2х+3 Поезд, двигаясь со скоростью
- 4. Область определения функции Все действительные числа Все действительные числа Х+1≠0 ⇒ Х≠-1 2х-6≥0 ⇒ 2х≥6 ⇒
- 5. Множество значений функции Все действительные числа у≥0 у≠0 у≥0 Множеством значений функции называют множество всех значений,
- 6. УКАЖИТЕ ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ОБЛАСТЬ ЗНАЧЕНИЙ ФУНКЦИИ. D(f) = [-3;3] E(f) = [-3;3]
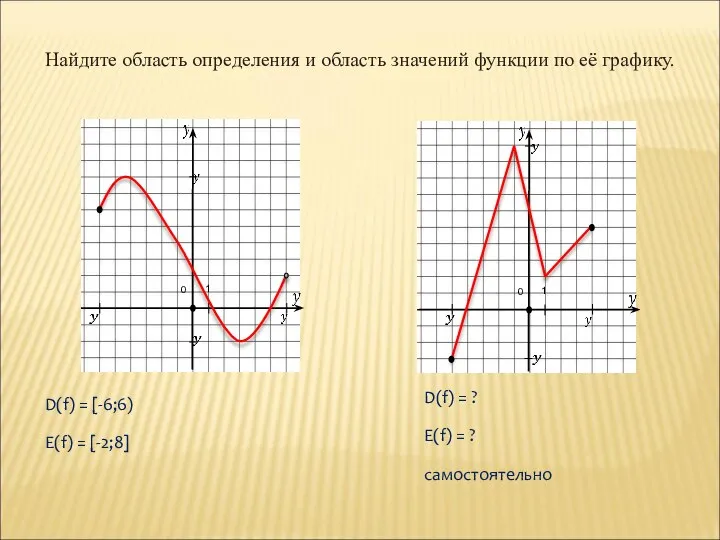
- 7. Найдите область определения и область значений функции по её графику. 0 1 0 1 D(f) =
- 8. ГРАФИК ФУНКЦИИ
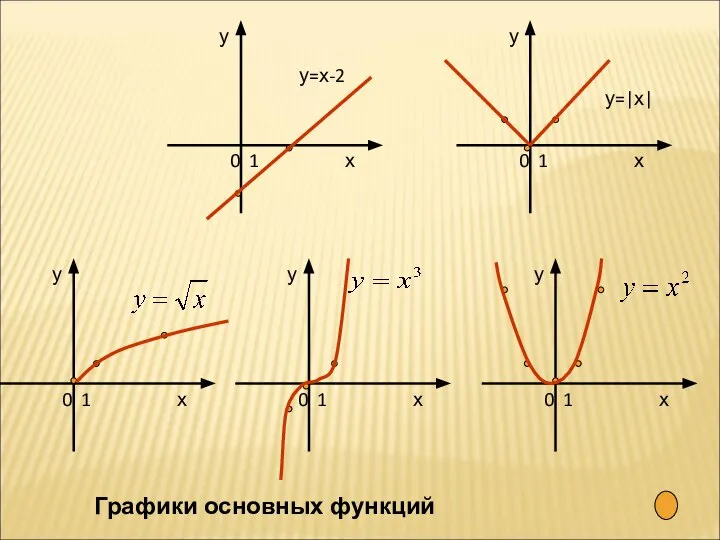
- 9. у=х-2 у=|х| Графики основных функций
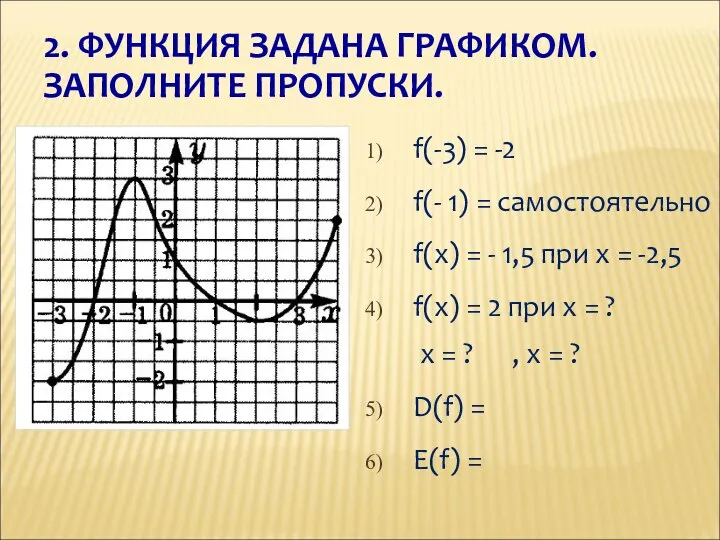
- 10. f(-3) = -2 f(- 1) = самостоятельно f(x) = - 1,5 при x = -2,5 f(x)
- 12. Скачать презентацию



![УКАЖИТЕ ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ОБЛАСТЬ ЗНАЧЕНИЙ ФУНКЦИИ. D(f) = [-3;3] E(f) = [-3;3]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/980552/slide-5.jpg)

 Второй признак подобия треугольников
Второй признак подобия треугольников Симметрия относительно прямой
Симметрия относительно прямой Отбор корней в тригонометрических уравнениях. Уравнения, имеющие ограничения в области определения
Отбор корней в тригонометрических уравнениях. Уравнения, имеющие ограничения в области определения Презентация на тему ГИА 2013. Модуль ГЕОМЕТРИЯ (№10)
Презентация на тему ГИА 2013. Модуль ГЕОМЕТРИЯ (№10)  Графический диктант. Тема: Делимость чисел
Графический диктант. Тема: Делимость чисел Презентация на тему СИСТЕМА ПОДГОТОВКИ УЧАЩИХСЯ К ЕГЭ ПО МАТЕМАТИКЕ
Презентация на тему СИСТЕМА ПОДГОТОВКИ УЧАЩИХСЯ К ЕГЭ ПО МАТЕМАТИКЕ 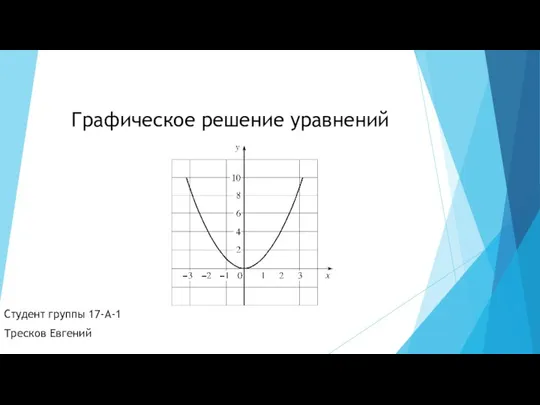 Графическое решение уравнений
Графическое решение уравнений Разложение функций
Разложение функций Таблица. Алгебра
Таблица. Алгебра Преобразование обыкновенных дробей в десятичные и десятичных в обыкновенные
Преобразование обыкновенных дробей в десятичные и десятичных в обыкновенные С математикой в космос
С математикой в космос Входная диагностика. 1 класс
Входная диагностика. 1 класс Презентация на тему Сложение и вычитание натуральных чисел (5 класс)
Презентация на тему Сложение и вычитание натуральных чисел (5 класс)  Конструирование из счётных палочек
Конструирование из счётных палочек Автоматы и алгоритмы. Комбинационные схемы и конечные автоматы
Автоматы и алгоритмы. Комбинационные схемы и конечные автоматы Математика-2
Математика-2 Луч. Дополнительные лучи. 5 класс
Луч. Дополнительные лучи. 5 класс Функции многих переменных. Лекция 16
Функции многих переменных. Лекция 16 Игровой тренажер
Игровой тренажер Алгоритмы решения простейших тригонометрических неравенств
Алгоритмы решения простейших тригонометрических неравенств Объем наклонной призмы. Теорема
Объем наклонной призмы. Теорема Тренировка интеллекта
Тренировка интеллекта Школьный портфель. Буква Ы. Счёт до 7
Школьный портфель. Буква Ы. Счёт до 7 Интерактивный тест по теме Виды треугольников
Интерактивный тест по теме Виды треугольников Случаи вычитания 15-
Случаи вычитания 15- Классические алгоритмы решения задачи точного совпадения
Классические алгоритмы решения задачи точного совпадения Прямоугольник, ромб, квадрат. Осевая и центральная симметрии
Прямоугольник, ромб, квадрат. Осевая и центральная симметрии Треугольники
Треугольники