Содержание
- 2. Понятие многогранника Л.С. Атанасян "Геометрия 10-11" Призма
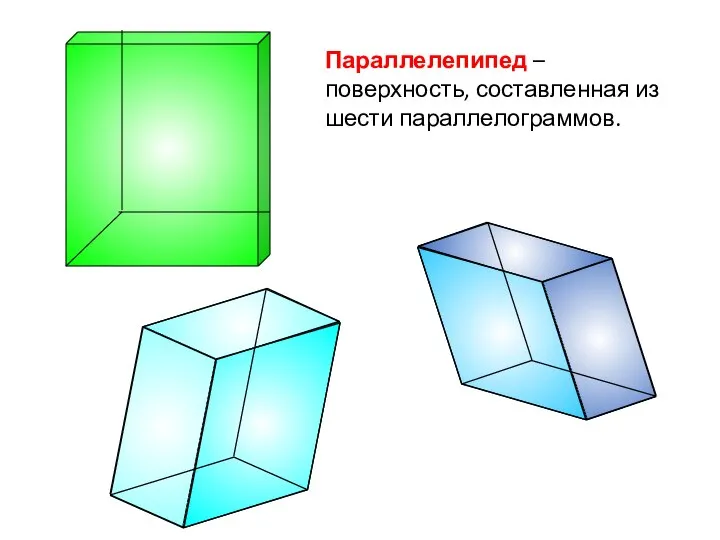
- 3. Параллелепипед – поверхность, составленная из шести параллелограммов.
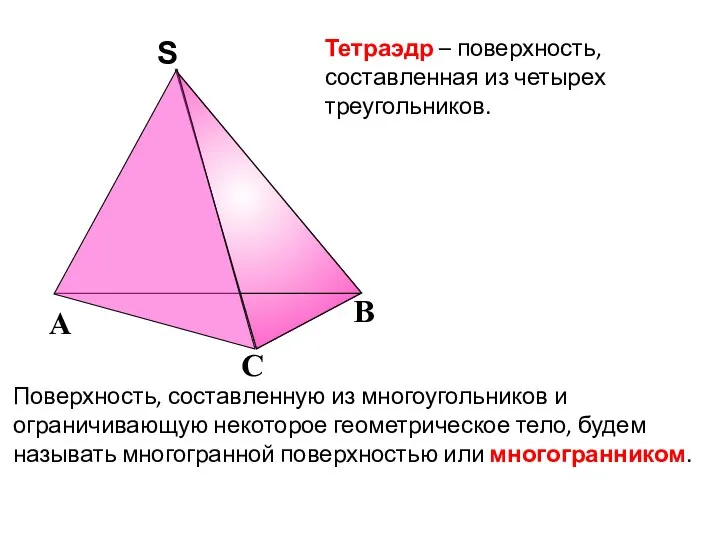
- 4. Тетраэдр – поверхность, составленная из четырех треугольников. Поверхность, составленную из многоугольников и ограничивающую некоторое геометрическое тело,
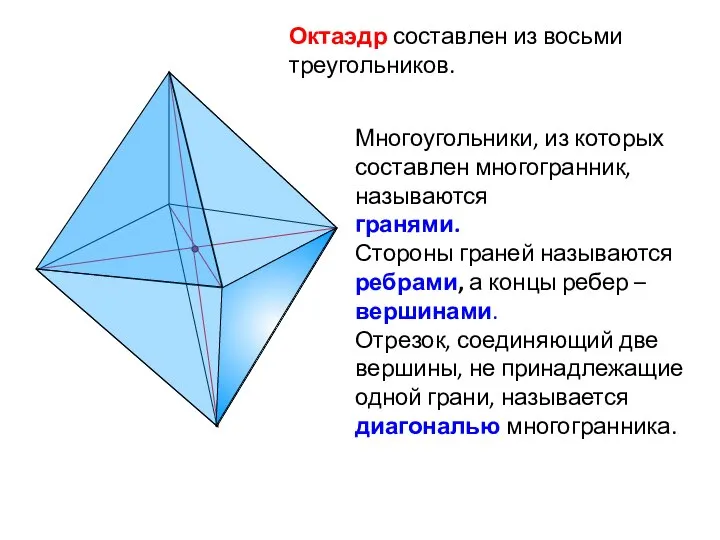
- 5. Октаэдр составлен из восьми треугольников. Многоугольники, из которых составлен многогранник, называются гранями. Стороны граней называются ребрами,
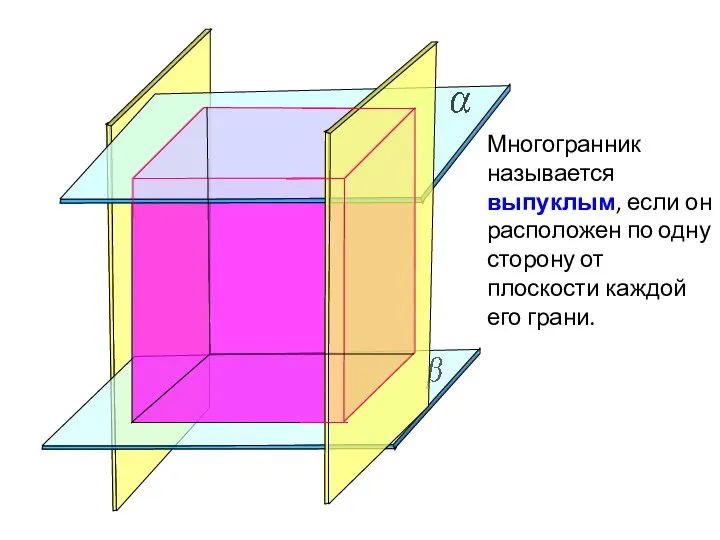
- 6. Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой его грани.
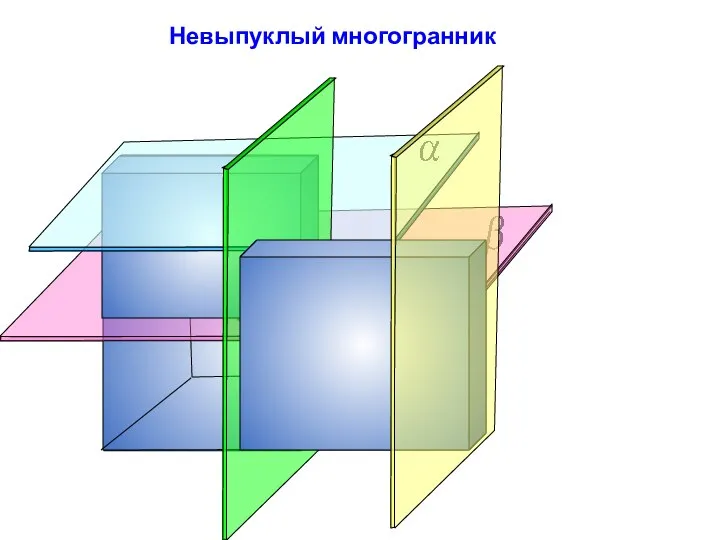
- 7. Невыпуклый многогранник
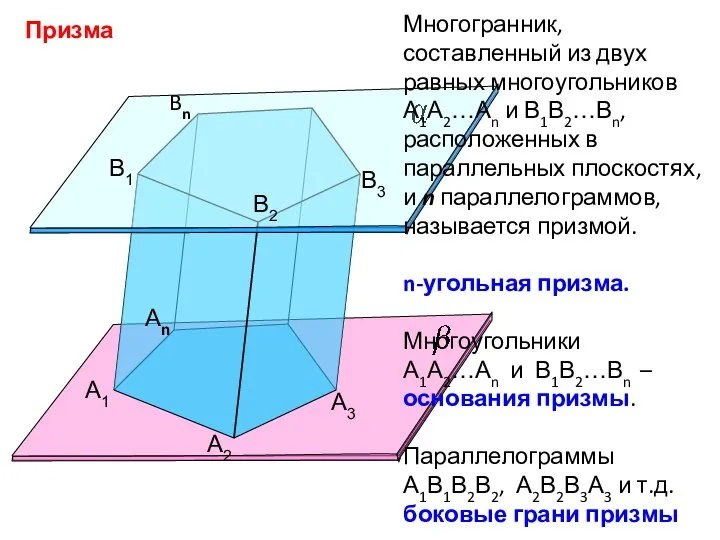
- 8. Призма А1 А2 Аn B1 B2 Bn B3 А3 Многогранник, составленный из двух равных многоугольников А1А2…Аn
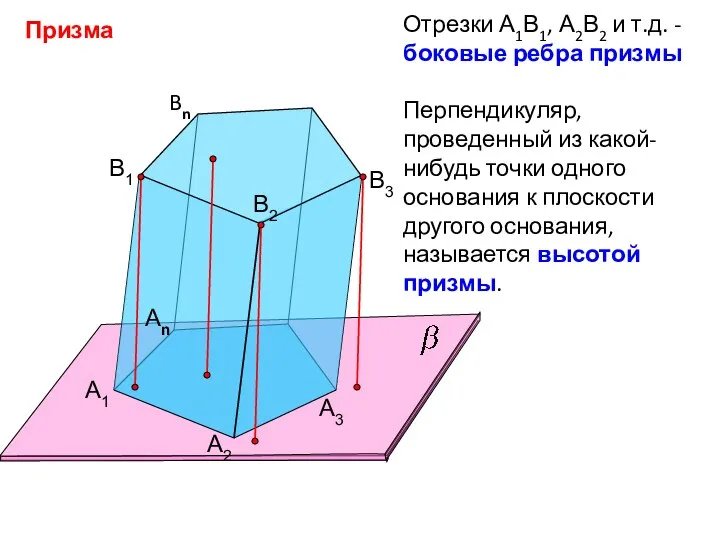
- 9. Призма А1 А2 Аn B1 B2 Bn B3 А3 Отрезки А1В1, А2В2 и т.д. - боковые
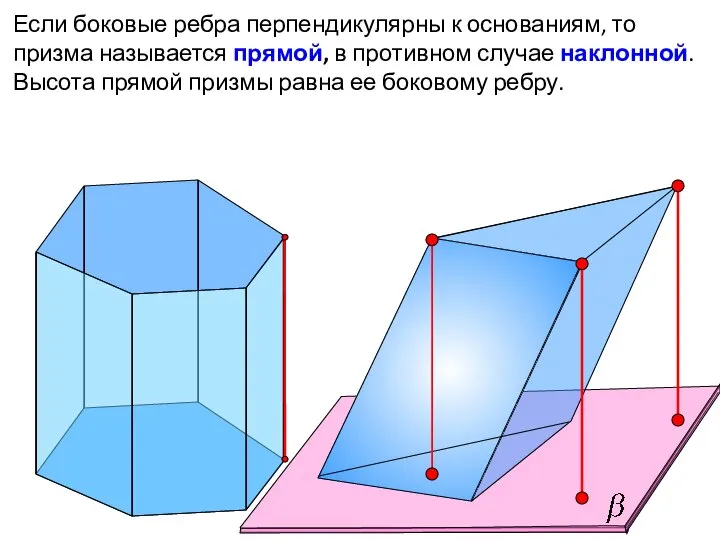
- 10. Если боковые ребра перпендикулярны к основаниям, то призма называется прямой, в противном случае наклонной. Высота прямой
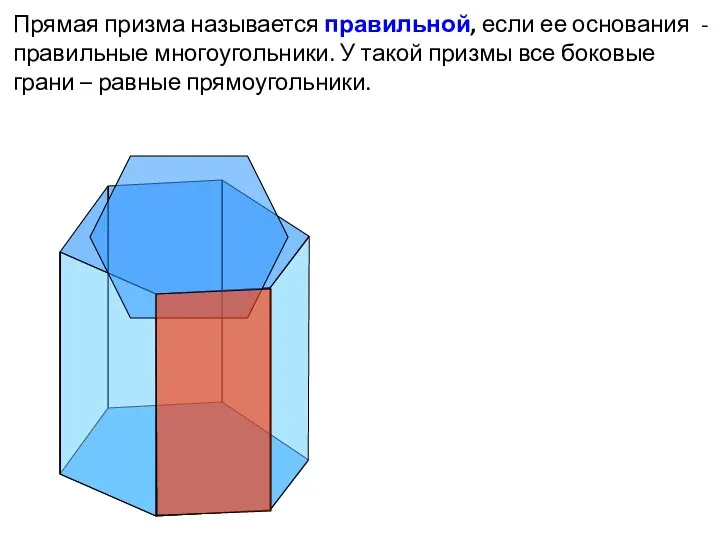
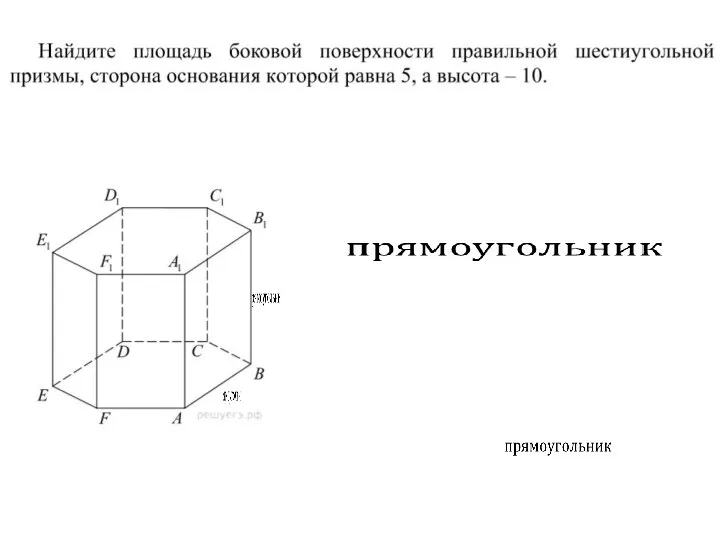
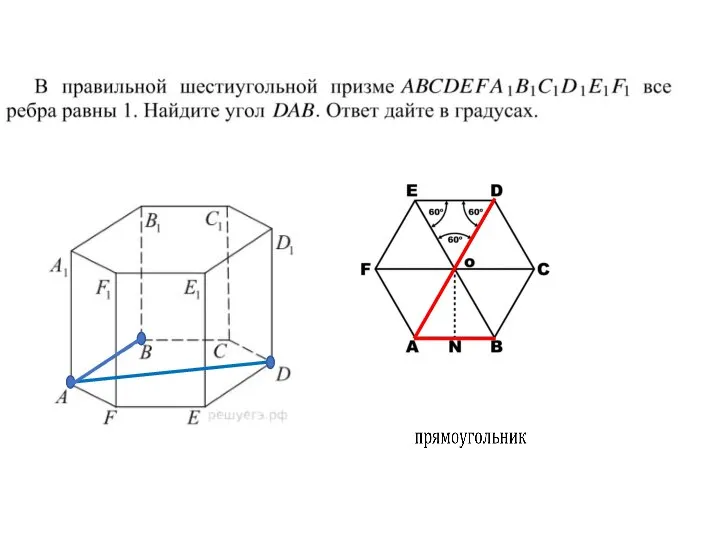
- 11. Прямая призма называется правильной, если ее основания - правильные многоугольники. У такой призмы все боковые грани
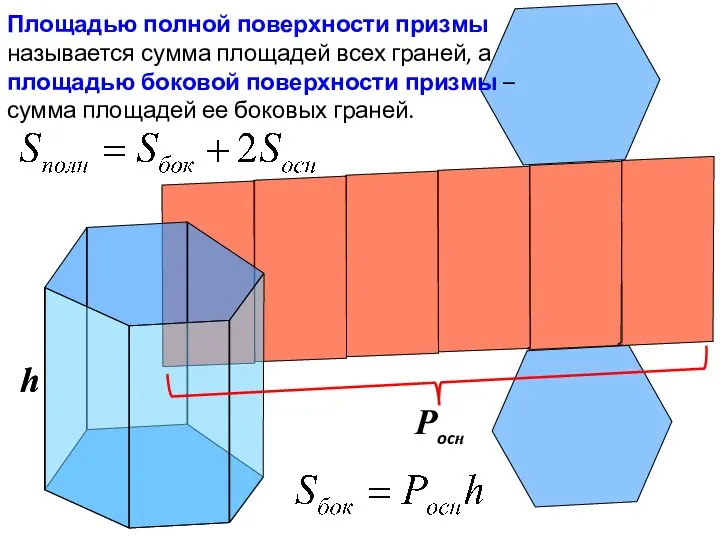
- 12. Площадью полной поверхности призмы называется сумма площадей всех граней, а площадью боковой поверхности призмы – сумма
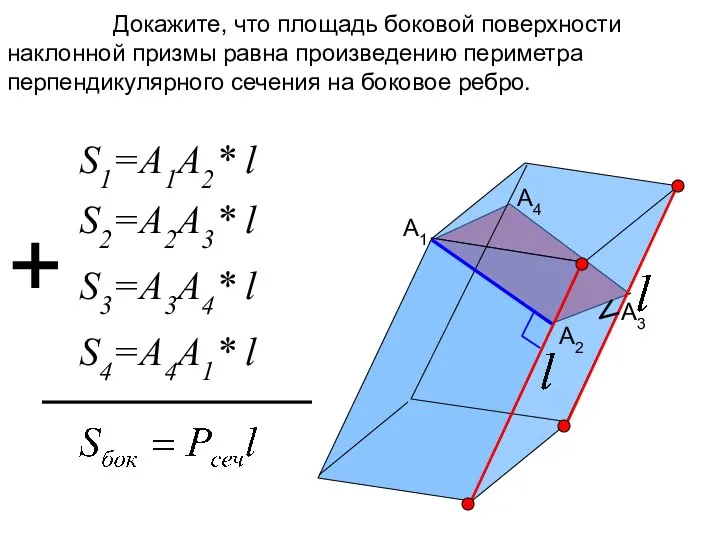
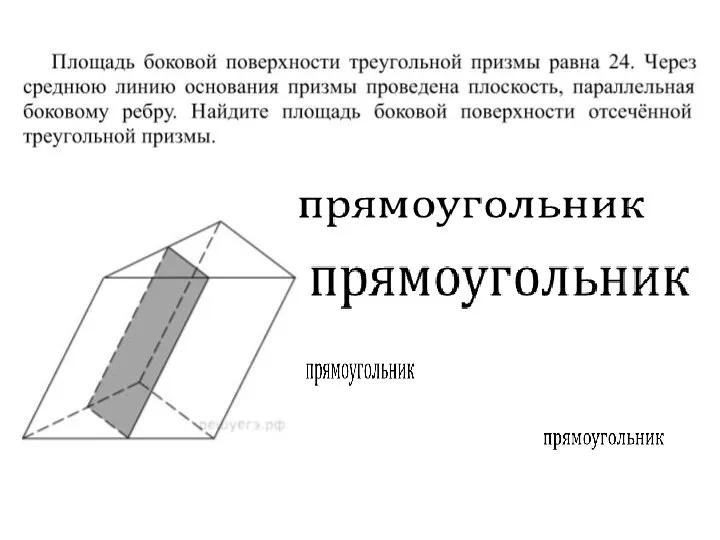
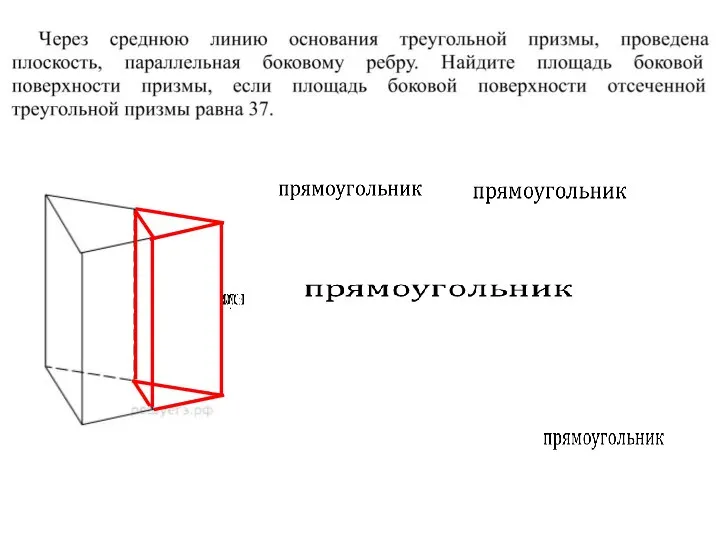
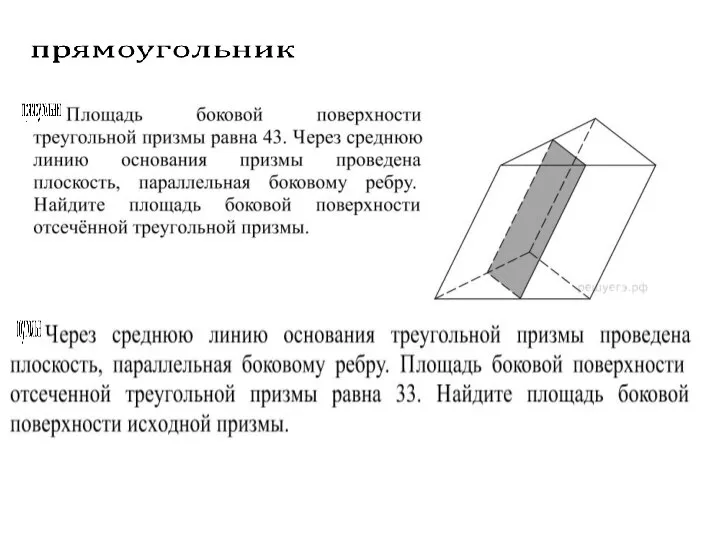
- 13. Докажите, что площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения на боковое ребро. A3
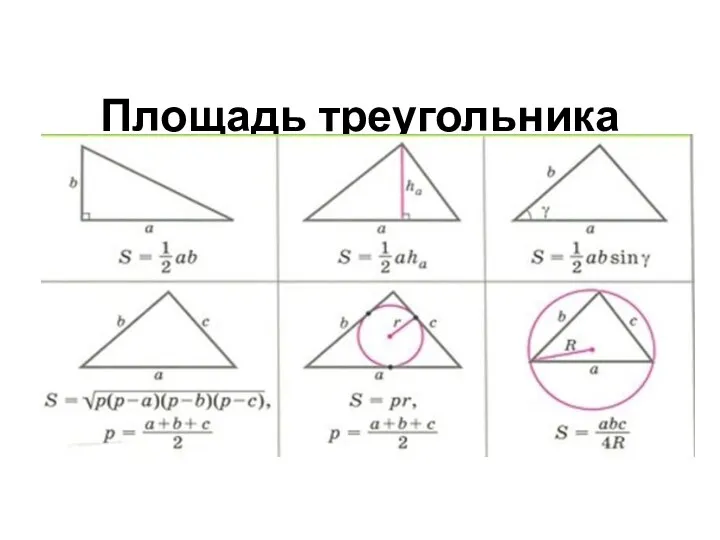
- 14. Площадь треугольника
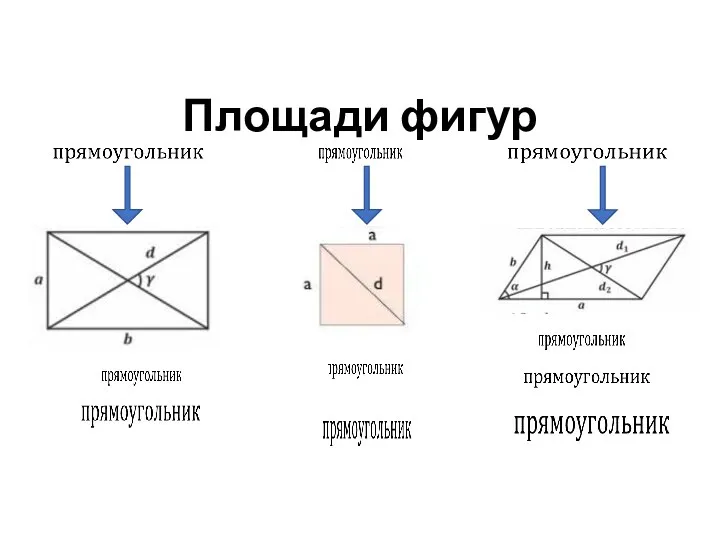
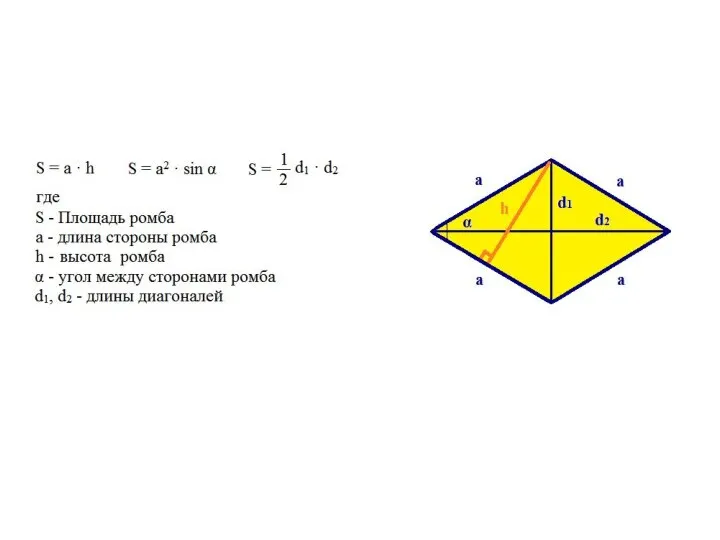
- 15. Площади фигур
- 17. Площадь трапеции
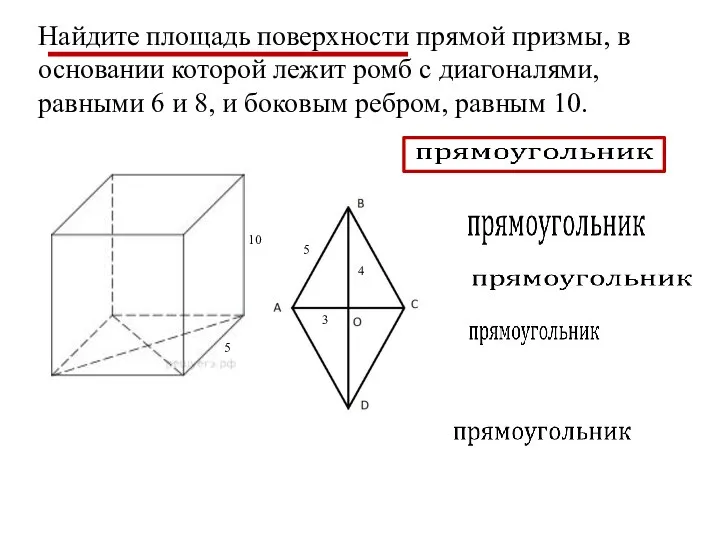
- 19. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8,
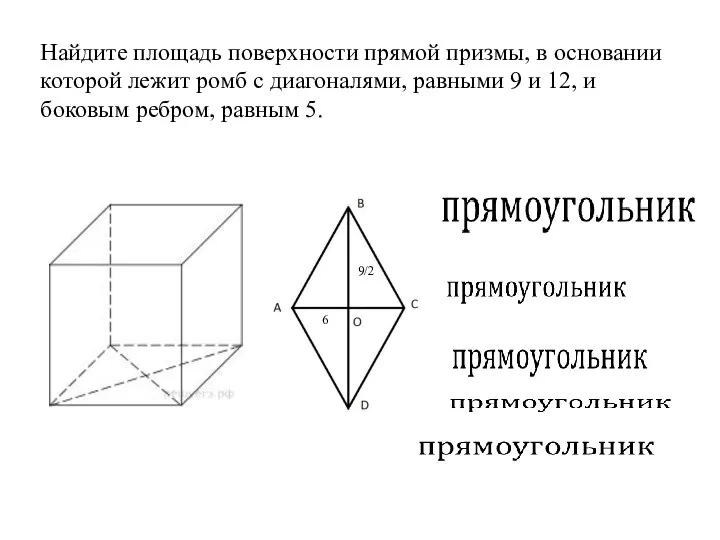
- 20. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 9 и 12,
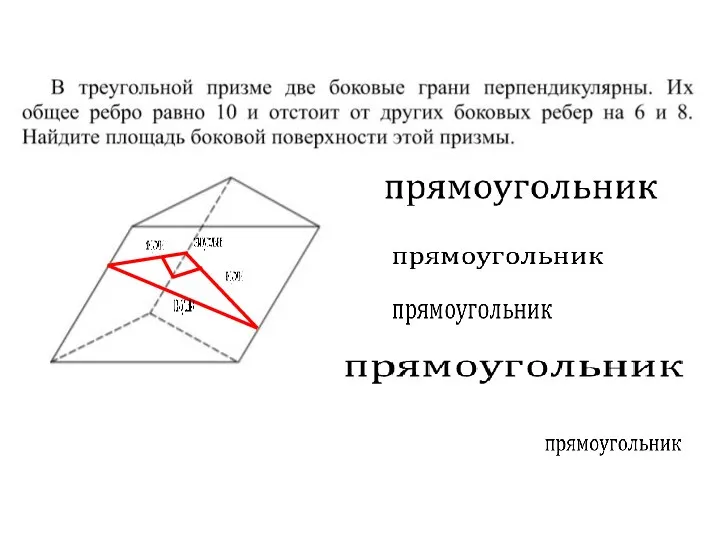
- 21. Найдите площадь боковой поверхности прямой призмы, в основании которой лежит прямоугольный треугольник с катетами, равными 5
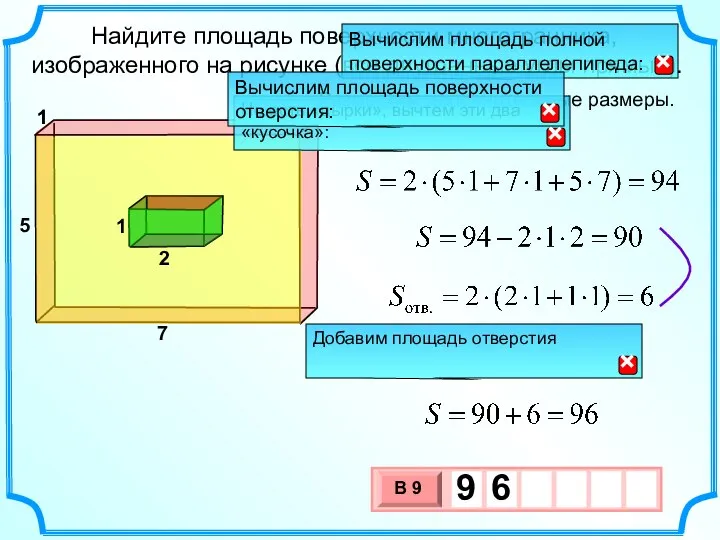
- 26. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). 5 Разместим дополнительные размеры. 5
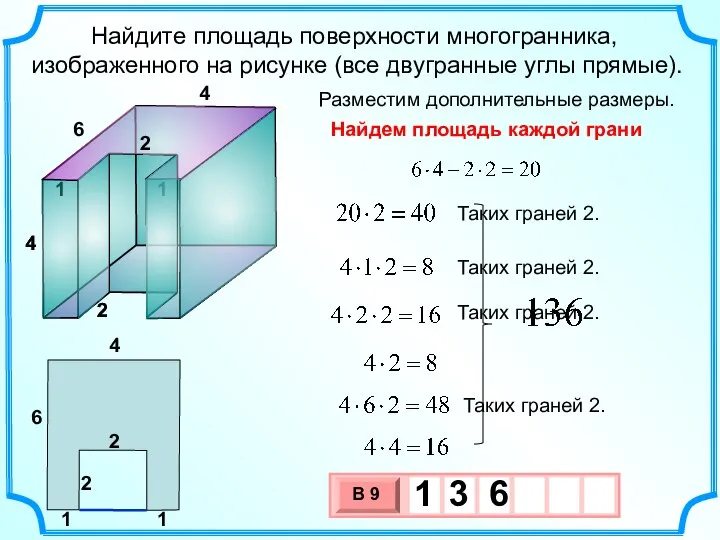
- 27. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). Разместим дополнительные размеры. 4 4
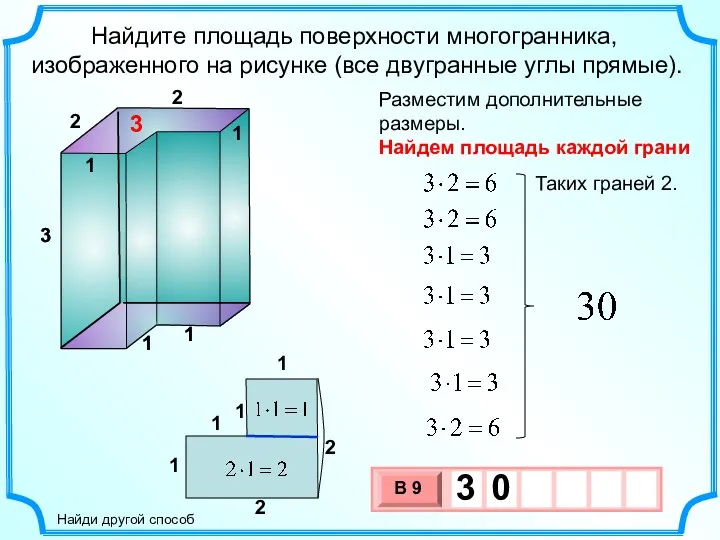
- 28. 3 Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). Разместим дополнительные размеры. 3
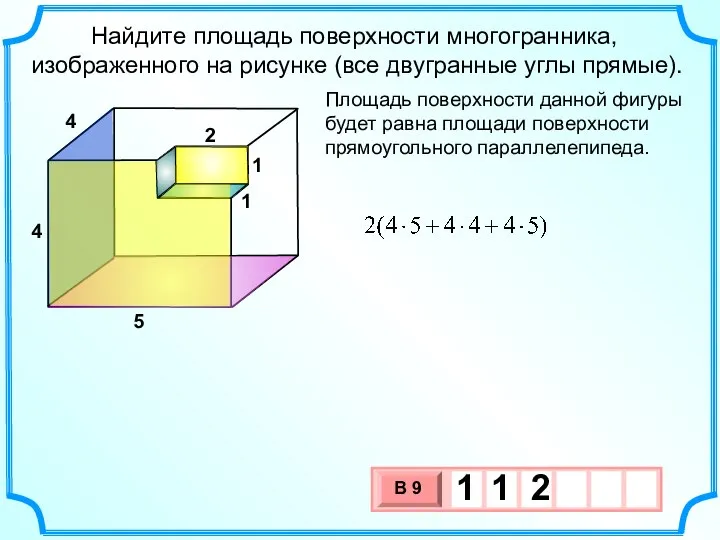
- 29. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). Площадь поверхности данной фигуры будет
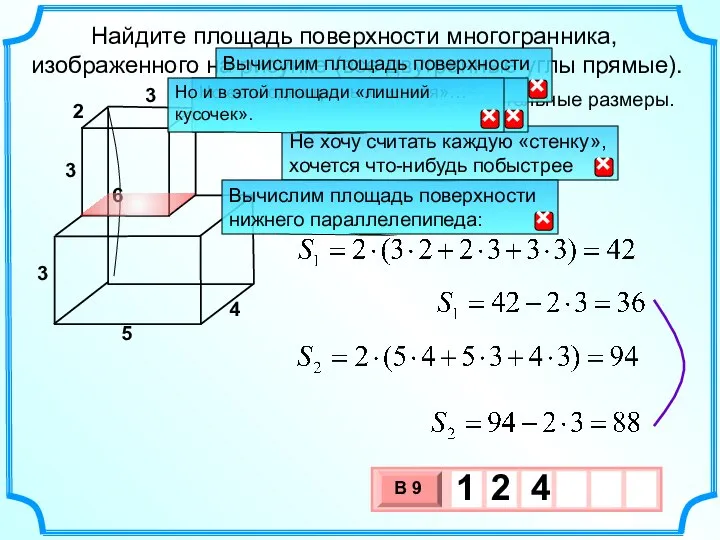
- 30. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). 4 3 1 1 2
- 31. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). Разместим дополнительные размеры. 1 1
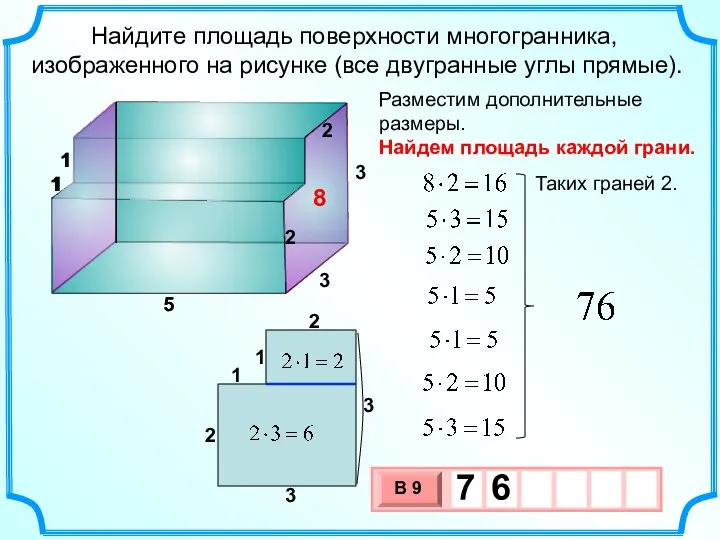
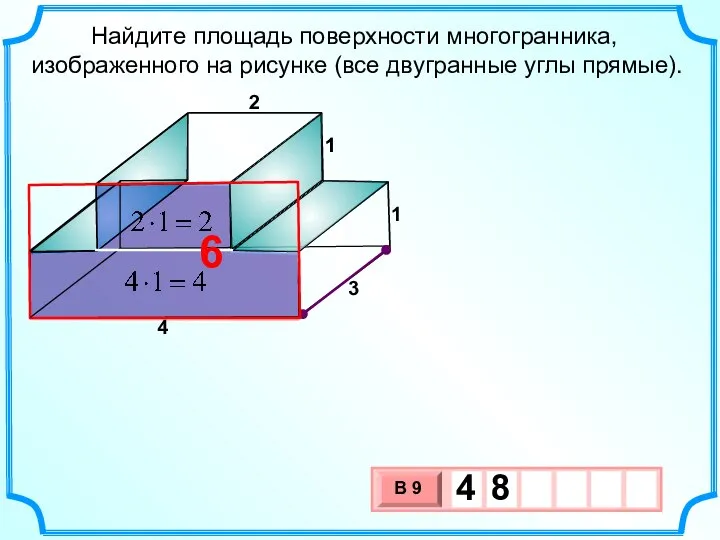
- 32. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). 2 3 3 6 4
- 39. Скачать презентацию







 Пределы. Раскрытие неопределенности. 2 часть
Пределы. Раскрытие неопределенности. 2 часть Погрешности измерительных приборов. Класс точности
Погрешности измерительных приборов. Класс точности Презентация на тему Круговые диаграммы (5 класс)
Презентация на тему Круговые диаграммы (5 класс)  Примеры комбинаторных задач
Примеры комбинаторных задач Векторы. 9 класс
Векторы. 9 класс Численные методы (траектория 1)
Численные методы (траектория 1) Полярные координаты
Полярные координаты Задачи по теме Циклический алгоритм
Задачи по теме Циклический алгоритм Метрология. Стандартизация
Метрология. Стандартизация Нахождение числа по доле и доли по числу
Нахождение числа по доле и доли по числу Эконометрика как наука
Эконометрика как наука Решение задач на движение
Решение задач на движение Множество. Сравнение множеств
Множество. Сравнение множеств Математическая модель
Математическая модель Выборочное наблюдение. Практическое занятие
Выборочное наблюдение. Практическое занятие algebr_drobi рабочая презентация начиная с 5 ссентября
algebr_drobi рабочая презентация начиная с 5 ссентября Статистическая обработка массива однородных величин. Практическое занятие 2
Статистическая обработка массива однородных величин. Практическое занятие 2 Презентация на тему График квадратичной функции Неравенства с одной переменной
Презентация на тему График квадратичной функции Неравенства с одной переменной  Презентация на тему Конкретный смысл действия умножения (2 класс)
Презентация на тему Конкретный смысл действия умножения (2 класс)  Средства измерений, классификация. Метрологические характеристики средств измерений
Средства измерений, классификация. Метрологические характеристики средств измерений Презентация на тему Элементы статистики
Презентация на тему Элементы статистики 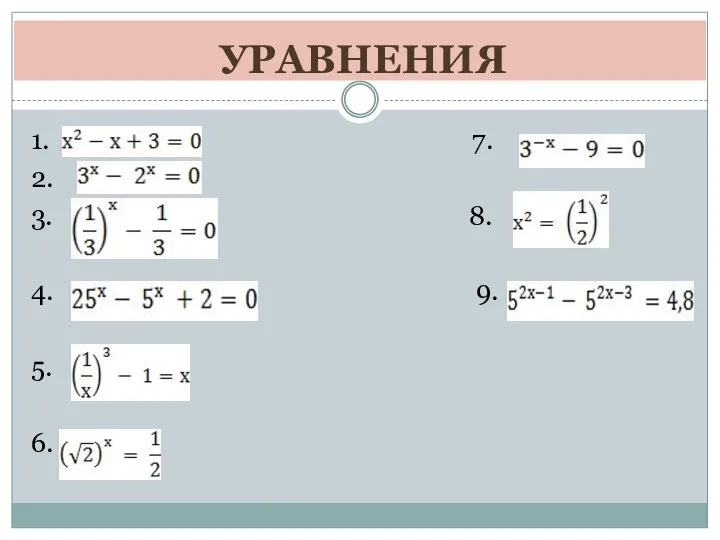 Решение показателей уравнений
Решение показателей уравнений Подготовка к тестированию
Подготовка к тестированию Презентация на тему Площади и объемы
Презентация на тему Площади и объемы  Презентация на тему Все о треугольниках
Презентация на тему Все о треугольниках  Состав числа в пределах 10; Компоненты задачи
Состав числа в пределах 10; Компоненты задачи Решение логических задач с помощью таблиц и метода рассуждений
Решение логических задач с помощью таблиц и метода рассуждений Тригонометрические функции числового аргумента
Тригонометрические функции числового аргумента