Свойства параллельных плоскостей (10 класс)

Тема урока «Свойства параллельных плоскостей».

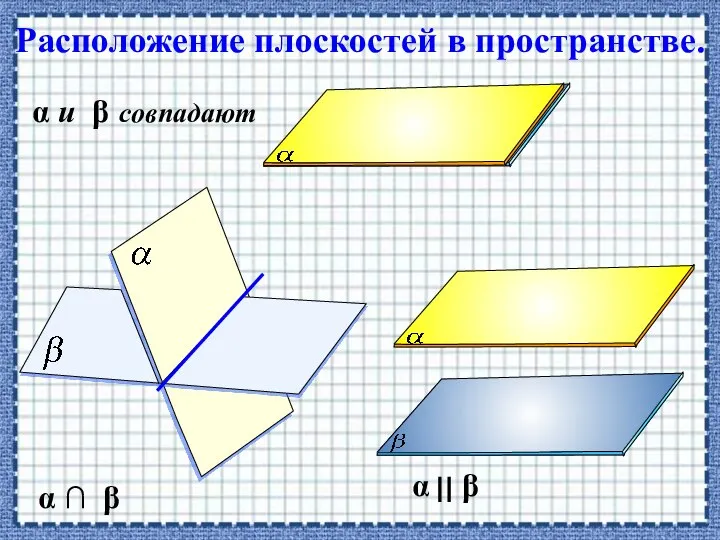
Расположение плоскостей в пространстве.
α ∩ β
α и β совпадают
α ⎜⎜ β

1. Какие плоскости называются параллельными?
2. На практике в столовой, где встречаетесь с параллельными плоскостями?
3. Сформулируйте признак параллельности плоскостей в пространстве.

Задание 1.
1. Плоскость α параллельна прямой в, а прямая в параллельна плоскости γ. Взаимное расположение плоскостей α и γ.
а) параллельны +
б) пересекаются +
в) совпадают +
2. Плоскость γ пересекает плоскости α и β по параллельным прямым а и в. Взаимное расположение плоскостей α и β.
а) параллельны +
б) пересекаются +
в) совпадают
3. Каждая из плоскостей α и β параллельна плоскости γ. Взаимное расположение плоскостей α и β.
а) параллельны +
б) пересекаются
в) совпадают
4. Каждая из плоскостей α и β параллельна прямой а. Взаимное расположение плоскостей α и β.
а) параллельны +
б) пересекаются +
в) совпадают +

Задание 2.
1. если плоскости не пересекаются, то они параллельны.
2. плоскости параллельны, если прямая лежащая в одной плоскости, параллельна другой плоскости
3. если две прямые, лежащие в одной плоскости, параллельны двум прямым другой плоскости, то эти плоскости параллельны
4. прямые, по которым две параллельные плоскости пересечены третьей плоскостью, параллельны.
5. Если прямая пересекает одну из двух плоскостей, то она пересекает и другую.
6. Отрезки прямых, заключенные между параллельными плоскостями, равны.
Да
Нет
Нет
Да
Нет
Нет
Определите: верно, ли утверждение?

Если две параллельные плоскости
пересечены третьей, то линии их пересечения параллельны.
Свойство параллельных плоскостей.
Дано:
α ⎜⎜ β, α ∩ γ = a
β ∩ γ = b
Доказать: a ⎜⎜ b
Доказательство:
1. a ⊂ γ, b ⊂ γ
2. Пусть a ⎜⎜ b,
тогда a ∩ b = М
3. M ∈ α, M ∈ β
⇒ α ∩ β = с (А2)
Получили противоречие с условием.
Значит a ⎜⎜ b ч. т.д.

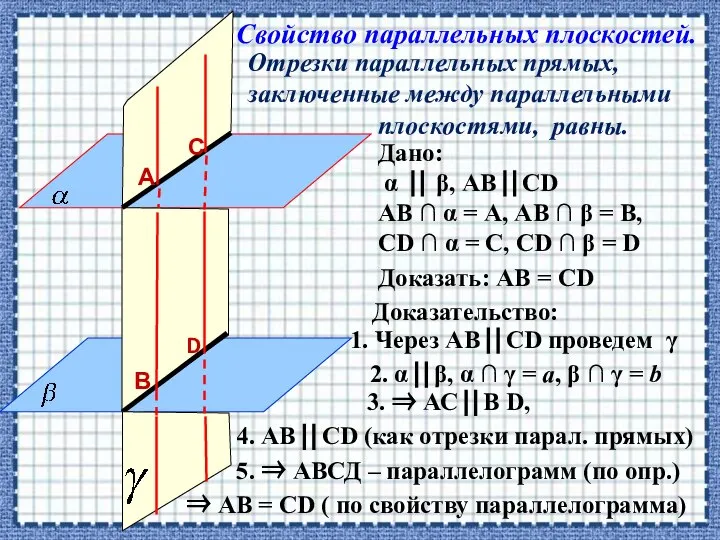
Отрезки параллельных прямых,
заключенные между параллельными
плоскостями, равны.
Свойство параллельных плоскостей.
Доказать: АВ = СD
Дано:
α ⎜⎜ β, АВ ⎜⎜СD
АВ ∩ α = А, АВ ∩ β = В,
СD ∩ α = С, СD ∩ β = D
Доказательство:
1. Через АВ ⎜⎜СD проведем γ
2. α ⎜⎜β, α ∩ γ = a, β ∩ γ = b
3. ⇒ АС ⎜⎜В D,
4. АВ ⎜⎜СD (как отрезки парал. прямых)
5. ⇒ АВСД – параллелограмм (по опр.)
⇒ АВ = СD ( по свойству параллелограмма)

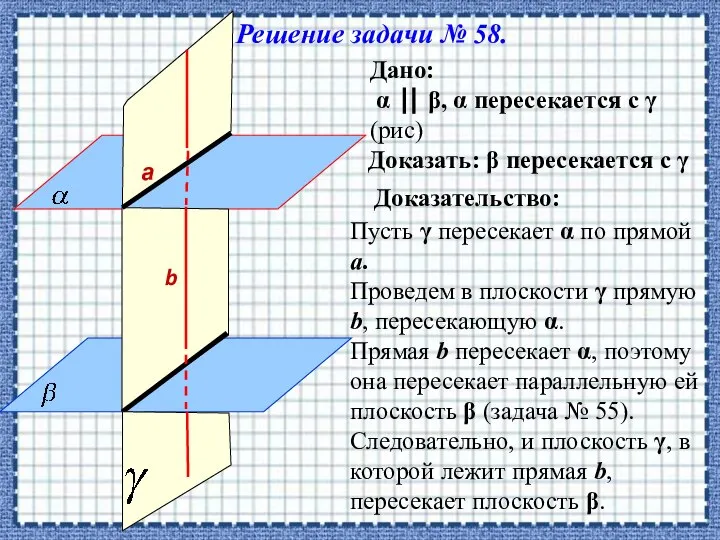
Решение задачи № 58.
Доказать: β пересекается с γ
Дано:
α ⎜⎜ β, α пересекается с γ (рис)
Доказательство:
Пусть γ пересекает α по прямой а.
Проведем в плоскости γ прямую b, пересекающую α.
Прямая b пересекает α, поэтому она пересекает параллельную ей плоскость β (задача № 55).
Следовательно, и плоскость γ, в которой лежит прямая b, пересекает плоскость β.

Самостоятельная работа

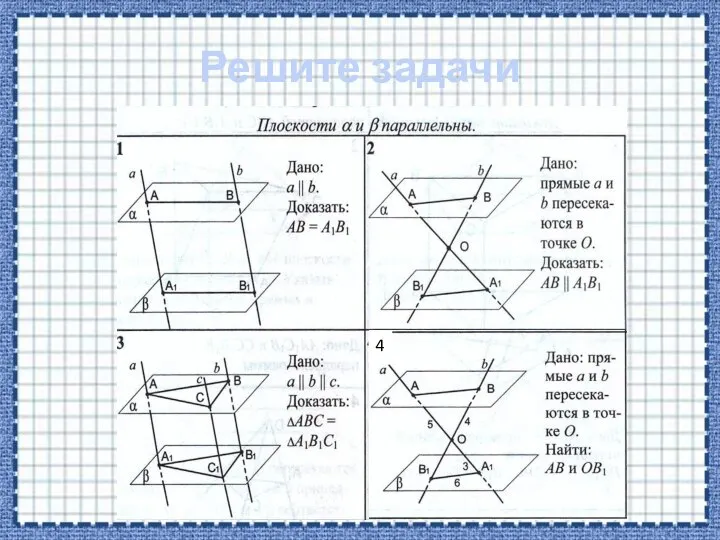
Решите задачи

Доказательство:
Рассмотрим четырехугольник АВВ1А1: АВ||А1В1 (по свойству 1), АА1||ВВ1 ( АА1 ϵ а, ВВ1 ϵ b, а||b), => АВВ1А1 – параллелограмм. В параллелограмме противоположные стороны равны. Значит, АВ = А1В1. Ч.т.д.
Доказательство:
Проведем плоскость γ ч/з пересекающиеся прямые а и b : γ∩α= АВ, γ∩β=А1В1.
По свойству 1: АВ||А1В1. Ч.т.д.