Содержание
- 2. q = quad (f, a, b) q = quad (f, a, b, tol) q = quad
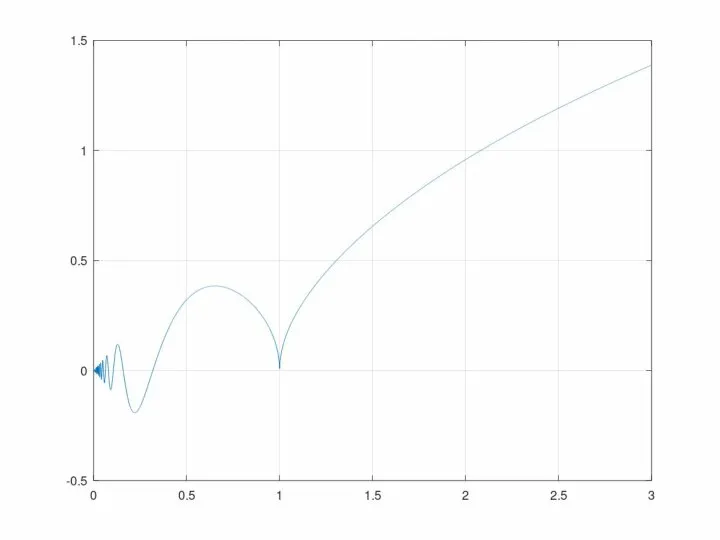
- 3. Вычислить интеграл: Напишем анонимную функцию: f=@(x)x .* sin (1./x) .* sqrt (abs (1 - x)) Построим
- 5. >> f=@(x)x .* sin (1./x) .* sqrt (abs (1 - x)) y=quad(f,0,3) ABNORMAL RETURN FROM DQAGP
- 6. Особенности интегрирования >> f=@(x)x.^-0.9 >> y=quad(f,0,1) y = 9.999999999999792 >> y=quadv(f,0,1) warning: quadv: minimum step size
- 7. Вычислить интеграл: >> f=(@(x) 1 ./ (sqrt (x) .* (x + 1)) >> quadgk(f, 0, Inf)
- 8. Интегрирование таблично заданных функций x=0:0.1:pi/2; y=sin(x); z=trapz (x, y) % Интегрирование методом % трапеций z=0.9966636 Рассмотрим
- 9. Вычисление интеграла с переменным верхним пределом Для вычисления такого интеграла надо составить файл-функцию вида: function y=Fax(f,a,x)
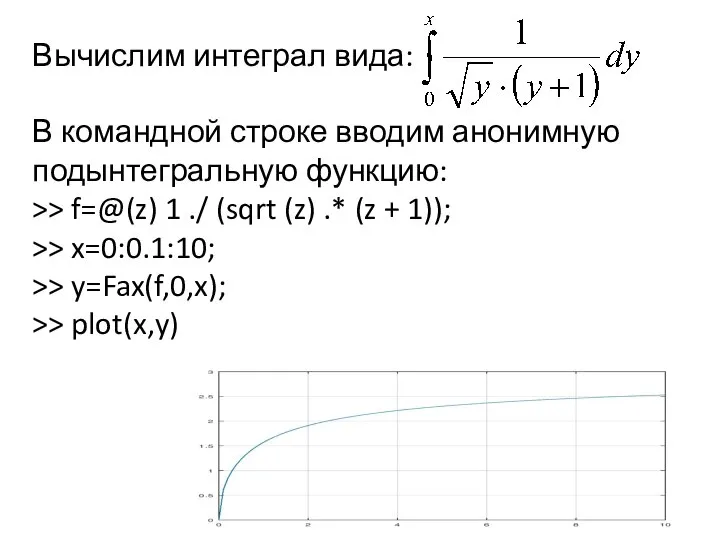
- 10. Вычислим интеграл вида: В командной строке вводим анонимную подынтегральную функцию: >> f=@(z) 1 ./ (sqrt (z)
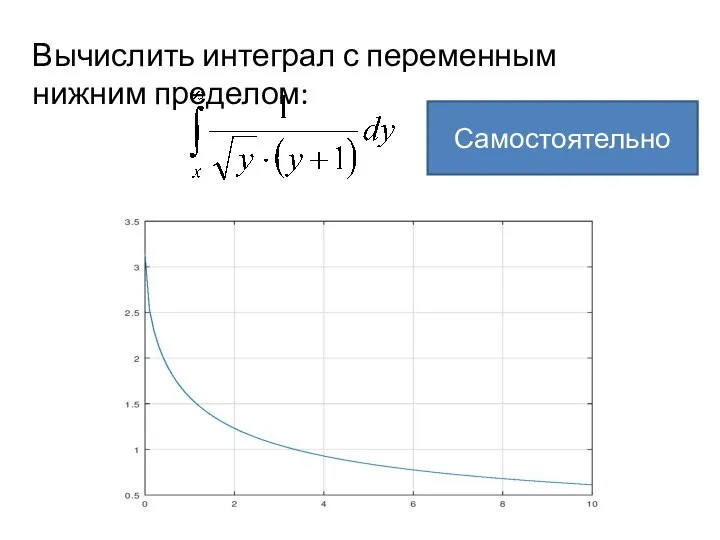
- 11. Вычислить интеграл с переменным нижним пределом: Самостоятельно
- 12. Двумерные интегралы Двумерные интегралы можно вычислять приведением двумерного интеграла к повторному (двумя способами). Особенностями двумерных интегралов
- 13. Вначале напишем функцию, вычисляющую внутренний интеграл по х при различных значениях y: function q = gint(y,a,b)
- 14. В командной строке найдем двумерный интеграл: >> ggint=@(x)gint(x,2,3);In=quadgk(ggint,0,1) In = 0.045377 Этот алгоритм осуществлен в функции
- 15. dblquad (f, xa, xb, ya, yb) dblquad (f, xa, xb, ya, yb, tol) dblquad (f, xa,
- 16. Примеры различных вызовов функции dblquad: >> f=@(x,y)sin(pi*x.*y).*sqrt(x.*y); >> format long; >> In=dblquad (f, 2, 3, 0,
- 17. Рекурсивный алгоритм для интегрирования, представленный выше, называется повторным интегрированием. Существует отдельный двумерный метод интегрирования, который осуществлен
- 18. q = quad2d (f, xa, xb, ya, yb) q = quad2d (f, xa, xb, ya, yb,
- 19. >> f=@(x,y)sin(pi*x.*y).*sqrt(x.*y); >> In=quad2d(f,2,3,0,1) In = 4.537731177584814e-02 Рассмотрим интегрирование по области в двумерном пространстве: y 0.5
- 20. Задание для самостоятельной работы Пусть необходимо построить график функции, которая задается следующей формулой: Собственные значения и
- 21. Исходные данные N=16 f1=0:1023 f2=0:7 T=0.002 df1=1 df2=3 P=1000 Выдать промежуточные данные: Построить график N/2 –й
- 23. Скачать презентацию

















 Решение линейных систем уравнений способом подстановки
Решение линейных систем уравнений способом подстановки Предельные теоремы ТВ
Предельные теоремы ТВ Кто хочет стать миллионером. Математическая игра
Кто хочет стать миллионером. Математическая игра Построение сечений параллелепипеда
Построение сечений параллелепипеда Назначение формулы
Назначение формулы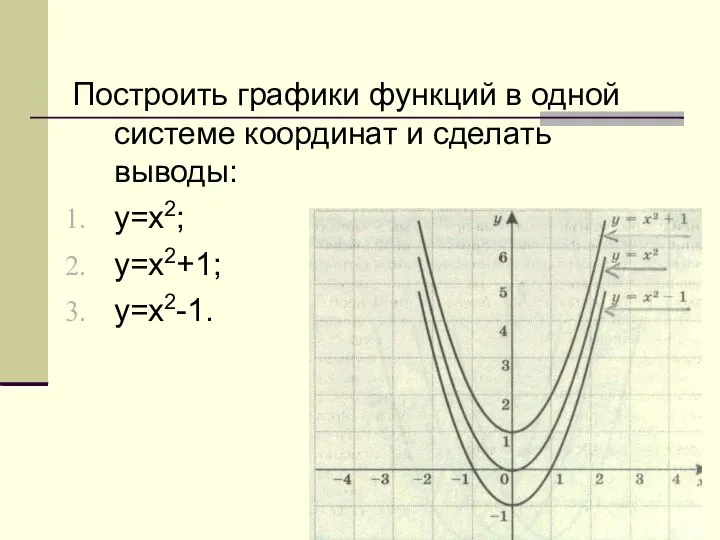 Графики функций в одной системе координат
Графики функций в одной системе координат Почти все об углах
Почти все об углах Анализ геометрической формы предмета (7 класс)
Анализ геометрической формы предмета (7 класс) Презентация на тему Занимательно о математике. Древняя нумерация, старинные меры длины, интересные цифры
Презентация на тему Занимательно о математике. Древняя нумерация, старинные меры длины, интересные цифры  Сводка и группировка данных статистического наблюдения
Сводка и группировка данных статистического наблюдения Презентация на тему Решение текстовых задач различными способами
Презентация на тему Решение текстовых задач различными способами  Деление взаимно обратных чисел
Деление взаимно обратных чисел Зачёт по таблице умножения
Зачёт по таблице умножения Построение угла по транспортиру. Задача
Построение угла по транспортиру. Задача Синус, косинус и тангенс угла
Синус, косинус и тангенс угла Задачи на части
Задачи на части Группы по одному или нескольким признакам
Группы по одному или нескольким признакам Презентация на тему Вертикальные и смежные углы
Презентация на тему Вертикальные и смежные углы  Числовые неравенства
Числовые неравенства Форматы вывода результата вычислений и логические операции в MATLAB
Форматы вывода результата вычислений и логические операции в MATLAB Треугольник паскаля
Треугольник паскаля Перпендикулярность плоскостей. Параллепипед
Перпендикулярность плоскостей. Параллепипед Сложение чисел. Тренажер, 1 класс
Сложение чисел. Тренажер, 1 класс В мире математики
В мире математики Решение треугольников
Решение треугольников Метод Крамера
Метод Крамера Теория Графов
Теория Графов Основы моделирования
Основы моделирования