Содержание
- 2. Цели Изучить формулы тангенса суммы и разности аргументов. Рассмотреть практическое применение данных формул.
- 3. Повторим Синус суммы двух аргументов равен произведению синуса первого аргумента на косинус второго плюс произведение косинуса
- 4. Повторим Косинус суммы двух аргументов равен произведению косинусов этих аргументов минус произведение синусов этих аргументов.
- 5. Повторим Синус разности двух аргументов равен произведению синуса первого аргумента на косинус второго минус произведение косинуса
- 6. Повторим Косинус разности двух аргументов равен произведению косинусов этих аргументов плюс произведение синусов этих аргументов.
- 7. Выведем формулу тангенса суммы двух аргументов По определению тангенс есть отношение синуса к косинусу одного и
- 8. Разделим числитель и знаменатель последней дроби на При всех допустимых значениях х и у
- 10. Получили: Аналогично можно доказать, что
- 11. Пример 1. Вычислить: Решение.
- 12. Пример 2. Вычислить: Решение.
- 13. Пример 3. Вычислить: Решение.
- 14. Историческая страничка
- 15. Замена хорд синусами стала главным достижением средневековой Индии. Такая замена позволила вводить различные функции, связанные со
- 16. Тригонометрия необходима для астрономических расчётов, которые оформляются в виде таблиц. Первая таблица синусов имеется в «Сурья-сиддхантеТригонометрия
- 17. Южноиндийские математики в XVI веке добились больших успехов в области суммирования бесконечных числовых рядов. В анонимном
- 18. Так, ряды для синуса и косинуса вывел Исаак НьютонТак, ряды для синуса и косинуса вывел Исаак
- 19. Джеймс Грегори Дата рождения: 1638 Место рождения: Драмоук, Шотландия Готфрид Вильгельм Лейбниц Дата рождения: 21 июня
- 20. С VIII века учёные стран Ближнего и Среднего Востока развили тригонометрию своих предшественников. В середине IX
- 21. После того как трактаты мусульманских ученых были переведены на латынь, многие идеи греческих, индийских и мусульманских
- 22. Решите из учебника № 20.1, 20.3, 20.5, 20.7
- 23. Задание на дом § 20 выучить № 20.2, 20.4, 20.6
- 25. Скачать презентацию







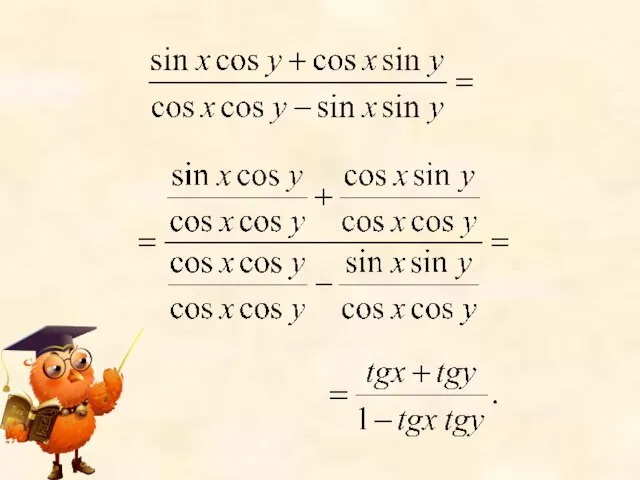













 Дюжина задач на параметры
Дюжина задач на параметры Ромб: признаки и свойства
Ромб: признаки и свойства Свойства биссектрисы угла. Решение задач
Свойства биссектрисы угла. Решение задач неопред интеграл
неопред интеграл Занятие 45. Формулы двойного угла. Формулы половинного угла
Занятие 45. Формулы двойного угла. Формулы половинного угла Центральная симметрия
Центральная симметрия Решение систем линейных неравенств с одной переменной (9 класс)
Решение систем линейных неравенств с одной переменной (9 класс) Практическое занятие №7 Минимизация логического автомата
Практическое занятие №7 Минимизация логического автомата Треугольники. Геометрия, 7 класс
Треугольники. Геометрия, 7 класс Вычитание смешанных чисел
Вычитание смешанных чисел Предмет стереометрии. Аксиомы стереометрии
Предмет стереометрии. Аксиомы стереометрии Окружность и её элементы
Окружность и её элементы Подготовка к ГИА. 9 класс
Подготовка к ГИА. 9 класс Формы представления регрессионных уравнений
Формы представления регрессионных уравнений Объем тела. Объем призмы, пирамиды, усечённой пирамиды
Объем тела. Объем призмы, пирамиды, усечённой пирамиды Арккосинус. Решение уравнений
Арккосинус. Решение уравнений Определители матриц
Определители матриц Презентация на тему Разложение многочлена на множители 7 класс
Презентация на тему Разложение многочлена на множители 7 класс  Пропорция. Пропорциональность и обратная пропорциональность
Пропорция. Пропорциональность и обратная пропорциональность Действия со степенями. Корень n-ой степени. Степень с рациональным показателем
Действия со степенями. Корень n-ой степени. Степень с рациональным показателем Восстанови ряд чисел
Восстанови ряд чисел Выборочное наблюдение
Выборочное наблюдение Метод наименьших квадратов. Ordinary Least Squares, OLS
Метод наименьших квадратов. Ordinary Least Squares, OLS Логарифмическая функция. Свойства, график. Решение примеров
Логарифмическая функция. Свойства, график. Решение примеров Согласование подходов к проверке заданий с развернутым ответом. Задания 22, 25
Согласование подходов к проверке заданий с развернутым ответом. Задания 22, 25 Storymaze. Побег
Storymaze. Побег Презентация на тему Число и цифра 5
Презентация на тему Число и цифра 5  Булева логика
Булева логика