Содержание
- 2. Множества Основные определения Алгебра множеств Представление множеств Вопросы
- 3. Множества. Основные определения Множество - это совокупность определенных различимых объектов, для каждого из которых можно установить,
- 4. Множества. Основные определения Способы задания множеств прямым перечислением всех элементов A = {a, b, c, …
- 5. Множества. Основные определения Универсальное множество или универсум есть множество U, состоящее из элементов всех рассматриваемых множеств.
- 6. Множества. Основные определения Мультимножество – совокупность элементов, в которые элементы входят по нескольку раз. расписание занятий
- 7. Множества. Алгебра множеств Сравнение множеств Множество A является подмножеством множества B, если любой элемент множества A
- 8. Множества. Алгебра множеств Мощность множеств. Сравнение мощностей Множество A называется собственным подмножеством множества B, если A
- 9. Множества. Алгебра множеств Мощность множеств. Сравнение мощностей Конечным называется такое множество A, у которого не существует
- 10. Множества. Алгебра множеств Операции над множествами Объединение A ∪ B = { x | x ∈
- 11. Множества. Алгебра множеств Объединение A ∪ B = { x | x ∈ A или x
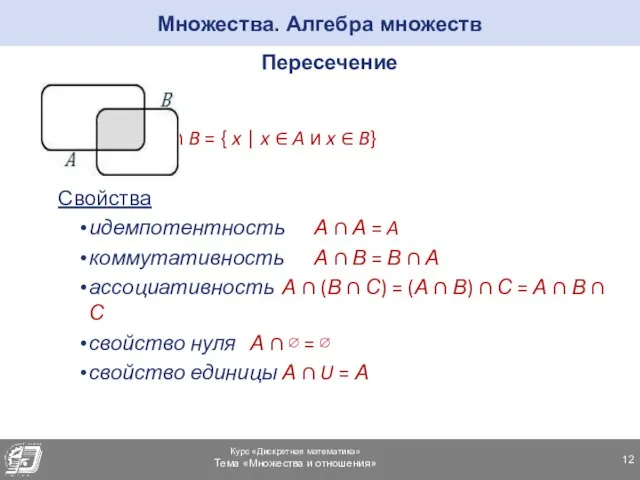
- 12. Множества. Алгебра множеств Пересечение A ∩ B = { x | x ∈ A и x
- 13. Множества. Алгебра множеств Разность B \ A = { x | x ∈ B и x
- 14. Множества. Алгебра множеств Симметрическая разность A ∆ B = (A ∪ B) \ (A ∩ B)
- 15. Множества. Алгебра множеств Разбиения. Покрытия Семейство множеств F = { Fi } называется покрытием множества B,
- 16. Множества. Алгебра множеств Булеан Булеаном множества А называется множество всех подмножеств множества А и обозначается как
- 17. Множества. Алгебра множеств Алгебра множеств – множество всех подмножеств множества U с операциями пересечения, объединения, разности
- 18. Множества. Алгебра множеств Законы алгебры множеств Дистрибутивный A ∩ (B ∪ C) = (A ∩ B)
- 19. Массив Связанный список Двоичный вектор Представление множеств
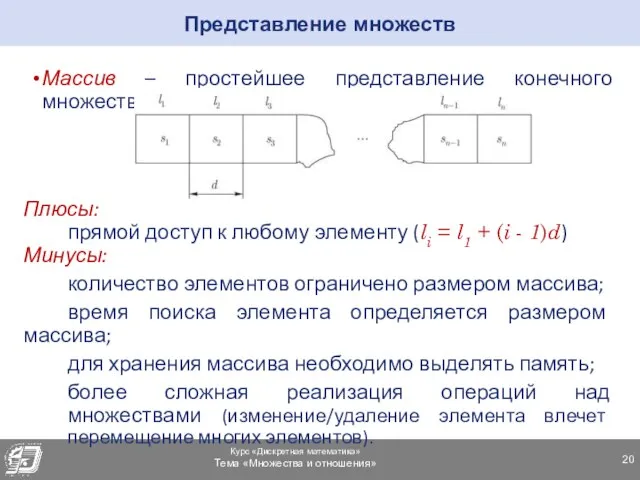
- 20. Массив – простейшее представление конечного множества, Плюсы: прямой доступ к любому элементу (li = l1 +
- 21. Характеристический вектор – разновидность последовательного распределения Длина вектора – мощность универсума |U| Пример: U = {1,
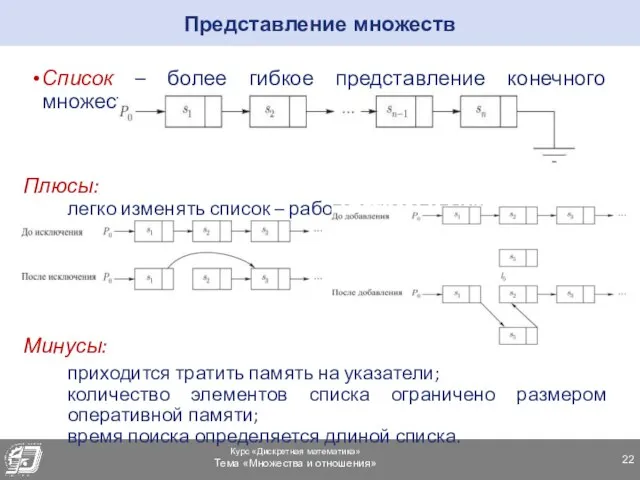
- 22. Список – более гибкое представление конечного множества, Плюсы: легко изменять список – работа с указателями Пример:
- 23. Словари (справочники) Хэш – таблицы (системы представителей) Очереди с приоритетами (задачи планирования) Базы данных (знаний) Применение
- 25. Скачать презентацию



















 Теоремы к зачёту
Теоремы к зачёту По следам теоремы Пифагора
По следам теоремы Пифагора Геометрический биатлон
Геометрический биатлон Комплексные числа
Комплексные числа Решение уравнений. 7 класс
Решение уравнений. 7 класс Основы логистики
Основы логистики Уравнения с двумя переменными
Уравнения с двумя переменными Веселый счет (Счет в прямом и обратном порядке в пределах 10)
Веселый счет (Счет в прямом и обратном порядке в пределах 10) Материал для внеклассной работы по математике. Бедный заяц (сказка)
Материал для внеклассной работы по математике. Бедный заяц (сказка) Числа, кратные 3
Числа, кратные 3 Прямые. Преобразование чертежа прямой. Две прямые
Прямые. Преобразование чертежа прямой. Две прямые Презентация на тему Пределы. Непрерывность функций
Презентация на тему Пределы. Непрерывность функций  Взаимно обратные числа
Взаимно обратные числа Тематические работы в форме ГИА (ЕГЭ)
Тематические работы в форме ГИА (ЕГЭ) Презентация на тему Простейшие задачи в координатах (9 класс)
Презентация на тему Простейшие задачи в координатах (9 класс)  Устный счёт. Закрепление изученного
Устный счёт. Закрепление изученного Презентация на тему Решение систем неравенств (9 класс)
Презентация на тему Решение систем неравенств (9 класс)  Считаем со смешариками. Тренажер Сложенеие и вычитание в пределах 10.Технологический прием Анимированная сорбонка
Считаем со смешариками. Тренажер Сложенеие и вычитание в пределах 10.Технологический прием Анимированная сорбонка Квадратные корни
Квадратные корни Математический калейдоскоп. Игра
Математический калейдоскоп. Игра График линейного уравнения с двумя переменными
График линейного уравнения с двумя переменными Регрессионный анализ
Регрессионный анализ Задания с фигурами
Задания с фигурами Второй признак подобия треугольников
Второй признак подобия треугольников Методика изучения Массы
Методика изучения Массы Функции одной и нескольких переменных
Функции одной и нескольких переменных Теория игр
Теория игр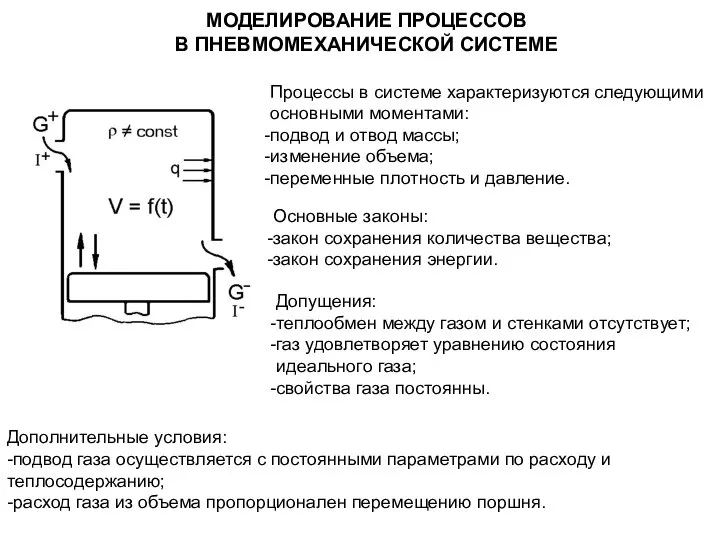 Моделирование процессов в пневмомеханической системе
Моделирование процессов в пневмомеханической системе