Содержание
- 2. Тема: «Цилиндр. Конус» Цели: расширить кругозор учащихся, углубить ЗУН учащихся по теме.
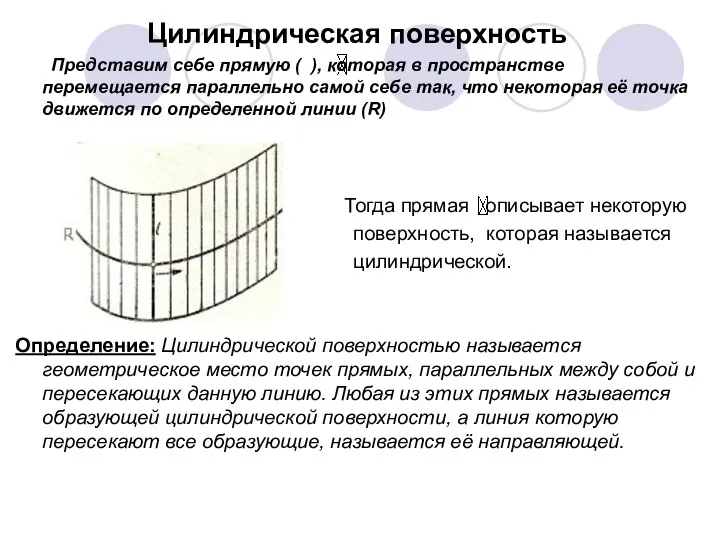
- 3. Цилиндрическая поверхность Представим себе прямую ( ), которая в пространстве перемещается параллельно самой себе так, что
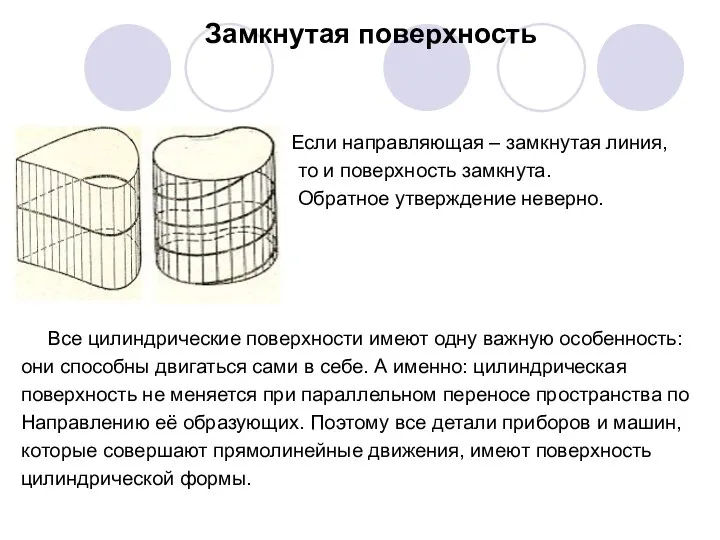
- 4. Замкнутая поверхность Если направляющая – замкнутая линия, то и поверхность замкнута. Обратное утверждение неверно. Все цилиндрические
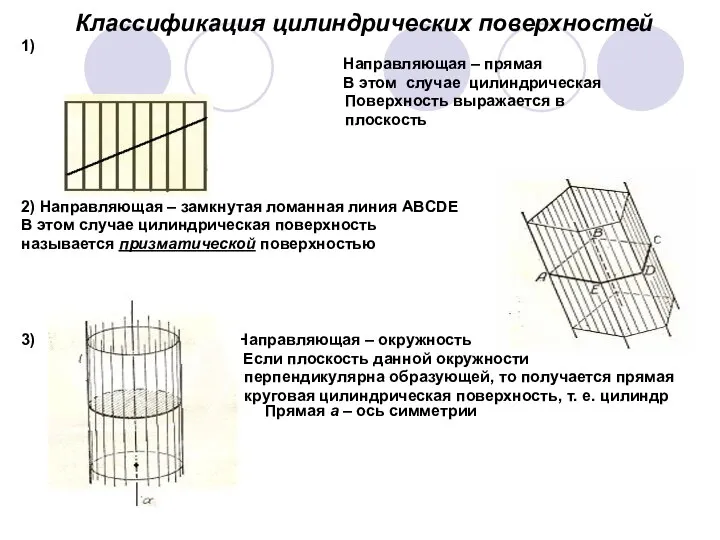
- 5. Классификация цилиндрических поверхностей 1) Направляющая – прямая В этом случае цилиндрическая Поверхность выражается в плоскость 2)
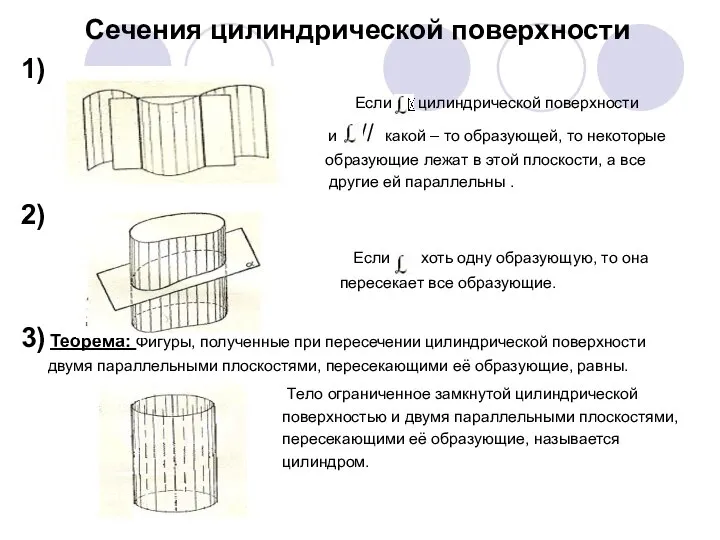
- 6. Сечения цилиндрической поверхности 1) Если цилиндрической поверхности и // какой – то образующей, то некоторые образующие
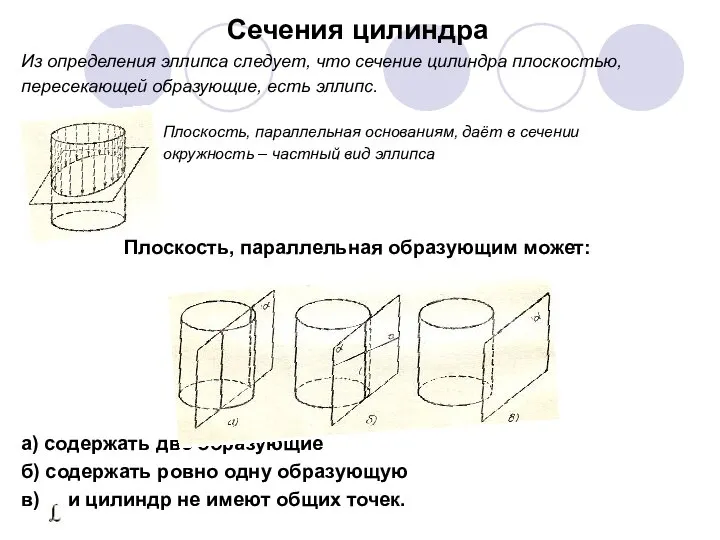
- 7. Сечения цилиндра Из определения эллипса следует, что сечение цилиндра плоскостью, пересекающей образующие, есть эллипс. Плоскость, параллельная
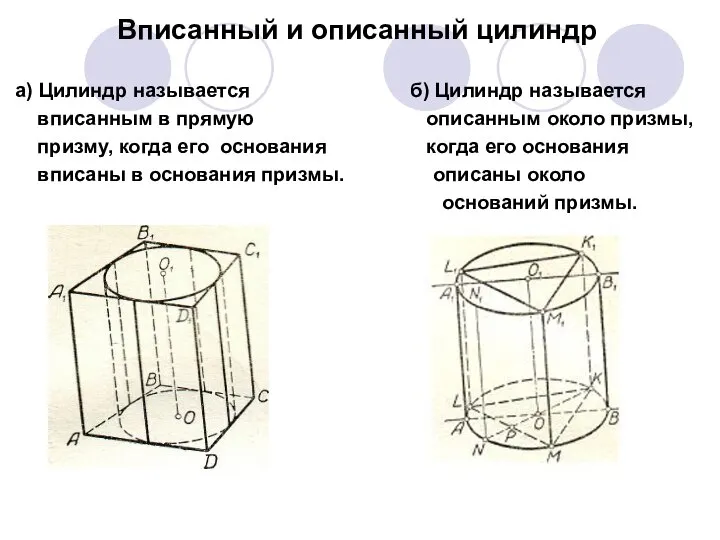
- 8. Вписанный и описанный цилиндр а) Цилиндр называется б) Цилиндр называется вписанным в прямую описанным около призмы,
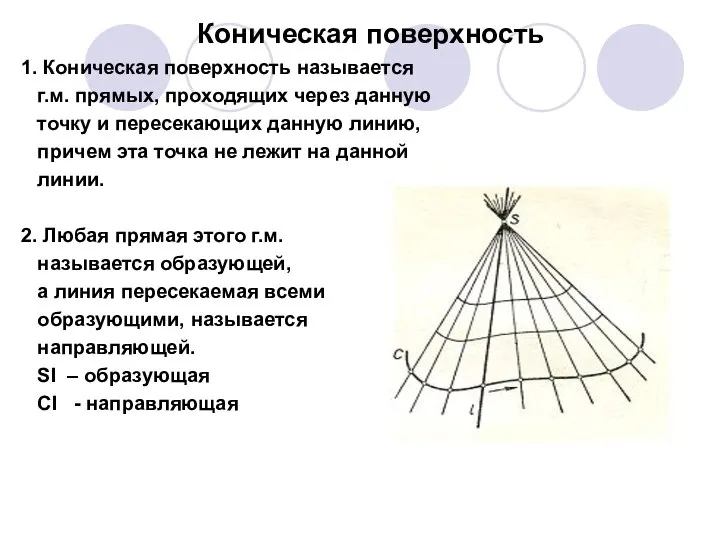
- 9. Коническая поверхность 1. Коническая поверхность называется г.м. прямых, проходящих через данную точку и пересекающих данную линию,
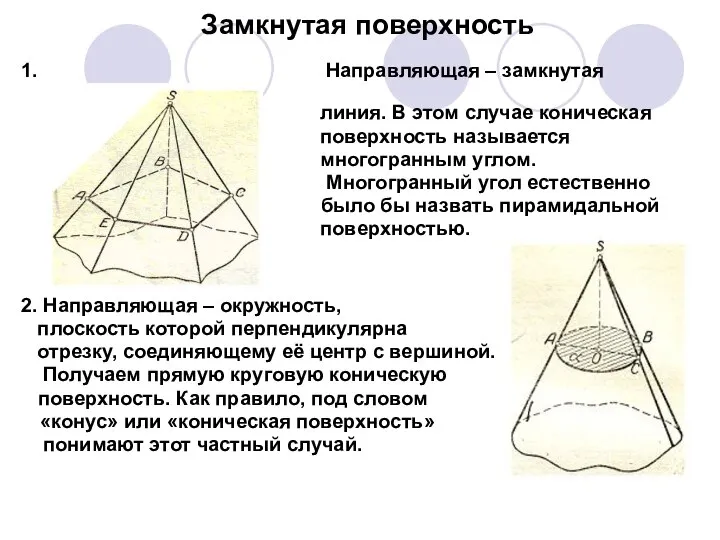
- 10. Замкнутая поверхность 1. Направляющая – замкнутая ломаная линия. В этом случае коническая поверхность называется многогранным углом.
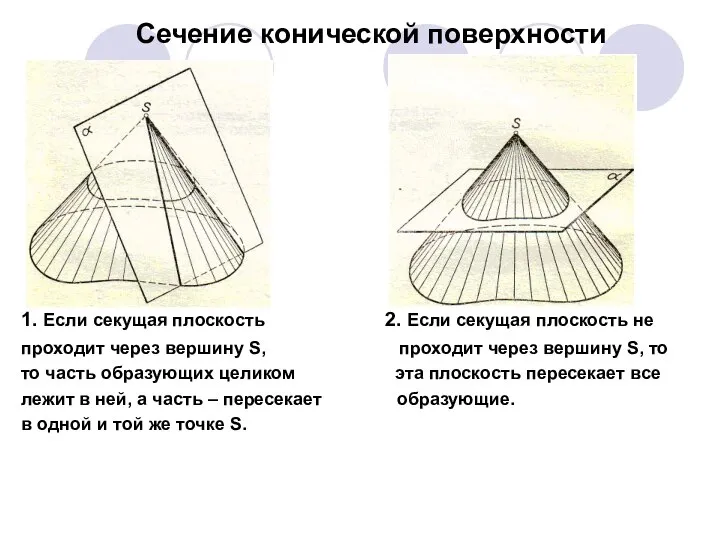
- 11. Сечение конической поверхности 1. Если секущая плоскость 2. Если секущая плоскость не проходит через вершину S,
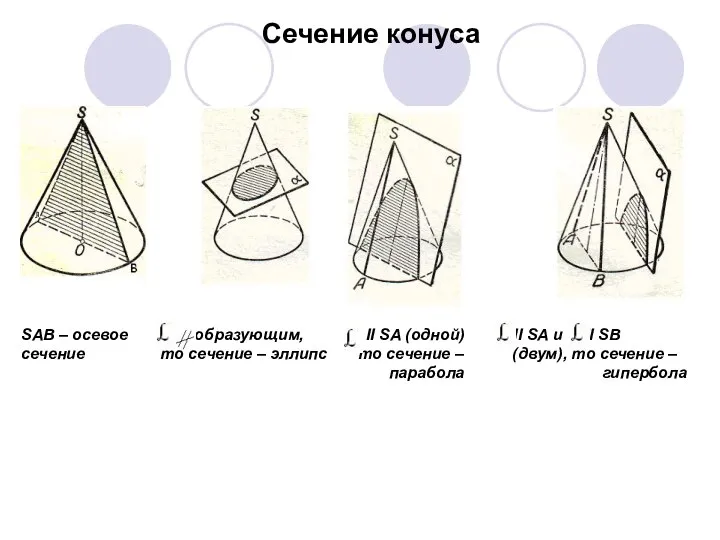
- 12. SAB – осевое образующим, II SA (одной) II SA и II SB сечение то сечение –
- 14. Скачать презентацию

 Теорема Пифагора
Теорема Пифагора Вывод формулы Герона. Геометрия 8 класс
Вывод формулы Герона. Геометрия 8 класс Coordinate plane
Coordinate plane Шар и сфера
Шар и сфера Применение производной
Применение производной Помогают законы. 5 - 7 класс
Помогают законы. 5 - 7 класс Многоугольник
Многоугольник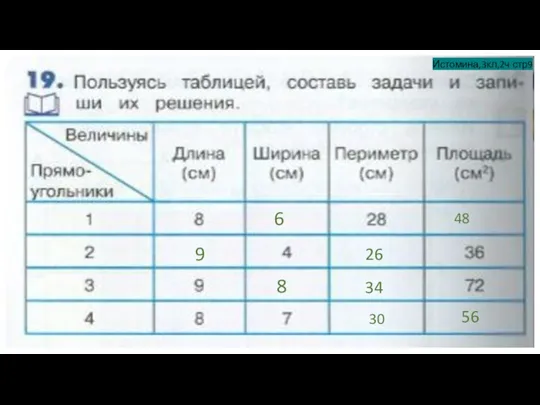 Величины. Составление задач
Величины. Составление задач Математика для дошкольников (средняя группа)
Математика для дошкольников (средняя группа) Кто живет под грибом
Кто живет под грибом Задачи для практики
Задачи для практики Введение в геометрию
Введение в геометрию Логическая задача. Способы решения
Логическая задача. Способы решения Презентация по математике "Величины. Объём" -
Презентация по математике "Величины. Объём" -  Презентация на тему Волейбол. Передача сверху
Презентация на тему Волейбол. Передача сверху  Алгебраическая дробь и её основное свойство. 7 класс
Алгебраическая дробь и её основное свойство. 7 класс Задачи на расстояния в пространстве
Задачи на расстояния в пространстве Как умножали египтяне
Как умножали египтяне Степень с натуральным показателем и его свойства
Степень с натуральным показателем и его свойства Презентация по математике "Число 7" -
Презентация по математике "Число 7" -  Симметрия в геометрии и в жизни
Симметрия в геометрии и в жизни Классификация функций
Классификация функций Математика
Математика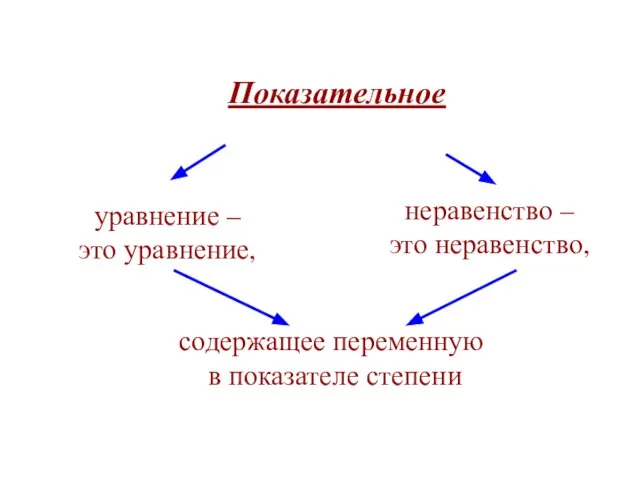 Показательное уравнение
Показательное уравнение Алгебра. Дроби. Сумма дробей
Алгебра. Дроби. Сумма дробей Координатная плоскость
Координатная плоскость Чётность и не чётность тригонометрических функций
Чётность и не чётность тригонометрических функций Числовая последовательность
Числовая последовательность