Слайд 4Иррациональные уравнения
Иррациональными называются уравнения, в которых переменная содержится под знаком

корня
Слайд 5 Иррациональные уравнения содержат радикалы. Чтобы избавиться от радикалов, необходимо возвести обе

части уравнения в одну и ту же степень с натуральным показателем.
Слайд 6если:
Возводим в нечетную степень, то получаем равносильное уравнение;
Возводим в четную степень,

то можем получить посторонние корни. В этом случае делаем проверку.
Слайд 7Алгоритм решения иррационального уравнения
Возвести обе части уравнения в квадрат.
Решить полученное рациональное уравнение.
Проверить

полученные корни подстановкой в исходное уравнение.
Выписать ответ.
Слайд 8Решить иррациональное уравнение

Слайд 9х2 –х-2=4
х2 –х - 6=0
х1=3
Проверка
Ответ: 3; -2
2=2
х2=

Слайд 10Решите уравнение, если оно имеет корни:
2











 Нахождение площади фигур и объемов тел
Нахождение площади фигур и объемов тел Задачи на уменьшение числа на несколько единиц
Задачи на уменьшение числа на несколько единиц Решение уравнений и неравенств с модулем
Решение уравнений и неравенств с модулем Собираемся в путешествие. Решение уравнений. Закрепление пройденного материала
Собираемся в путешествие. Решение уравнений. Закрепление пройденного материала Нахождение корней уравнения с помощью подбора параметра
Нахождение корней уравнения с помощью подбора параметра повторение 7-9
повторение 7-9 Сложение и вычитание трёхзначных чисел. Геометрическое задание
Сложение и вычитание трёхзначных чисел. Геометрическое задание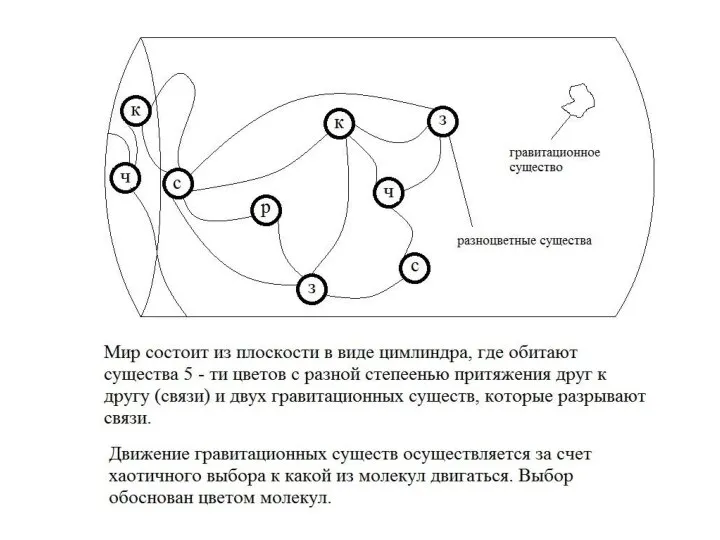 Мир в поверхности цилиндра
Мир в поверхности цилиндра Случайные сигналы и их математические модели
Случайные сигналы и их математические модели Состав числа 5
Состав числа 5 Натуральные числа. Викторина
Натуральные числа. Викторина Признаки равенства треугольников
Признаки равенства треугольников Понятие о комплексных числах. Рациональные функции одной переменной
Понятие о комплексных числах. Рациональные функции одной переменной Четырехугольники
Четырехугольники Комплексные числа
Комплексные числа Дроби
Дроби Тренажер. Единицы площади
Тренажер. Единицы площади Применение инверсии при построении графиков
Применение инверсии при построении графиков Лабораторно-практическая работа в парах
Лабораторно-практическая работа в парах Математика, Устный счёт
Математика, Устный счёт Вычисление площадей фигур с помощью интеграла
Вычисление площадей фигур с помощью интеграла Знаки тригонометрических функций. Формулы сложения
Знаки тригонометрических функций. Формулы сложения Предел последовательности. Бесконечно убывающая геометрическая прогрессия
Предел последовательности. Бесконечно убывающая геометрическая прогрессия Танграм (древняя китайская головоломка)
Танграм (древняя китайская головоломка) Урок по теме: Умножение десятичной дроби на 10, 100, 1000… по учебнику "Математика", Зубарева И.И., Мордкович А.Г.: Учебник для 5 класса общеобразовательных учреждений
Урок по теме: Умножение десятичной дроби на 10, 100, 1000… по учебнику "Математика", Зубарева И.И., Мордкович А.Г.: Учебник для 5 класса общеобразовательных учреждений Векторы в пространстве
Векторы в пространстве Тригонометрические функции. Их свойства и график (1)
Тригонометрические функции. Их свойства и график (1) Математическая логика. Логические выражения
Математическая логика. Логические выражения